“连接体问题”命题规律研究和教学策略

摘  要：“连接体”问题蕴含了较多的知识点，涉及多个运动模型，考查多种物理思想方法，广受命题人的青睐。本文利用统计的方法，以近八年江苏高考卷为例，从试题在各类题型中的分布、试题分值、对象模型、运动模型、涉及的物理方法和处理观点这六个方面进行分析，同时，结合学生在该类问题中的常见学习误区，提出三个教学建议。

关键词：连接体;命题规律;学情分析;应对策略

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2015）9-0016-3

“连接体”问题蕴含了较多的物理知识和方法，是学生学习中的重点和难点，也是高考中的热点，在历年的各地高考试卷中均有所涉及，不断发挥着其选择和甄别的功能。本文以江苏卷为例，利用统计法，从六个方面对江苏2008年实施高考新方案以来，8年高考试卷中所涉及的“连接体”问题进行探讨，同时，依据自身对学生学习情况的把握，就该类问题的教学策略提出一些看法，以期能对教学有所帮助。

1    考情分析

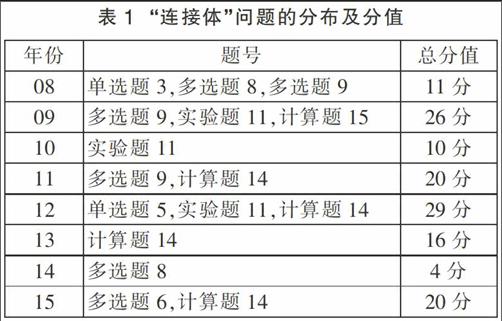
1.1    试题分布和分值的统计

从八年的高考试卷看，涉及“连接体”问题的试题共16道，按年份看，此类试题的题型、分值分布情况如表1所示。由该表可知，“连接体”问题在“多选题”中出现比重最大（约占总量的37.5%），在“单选题”中的比重最小（约占总量的12.5%）。

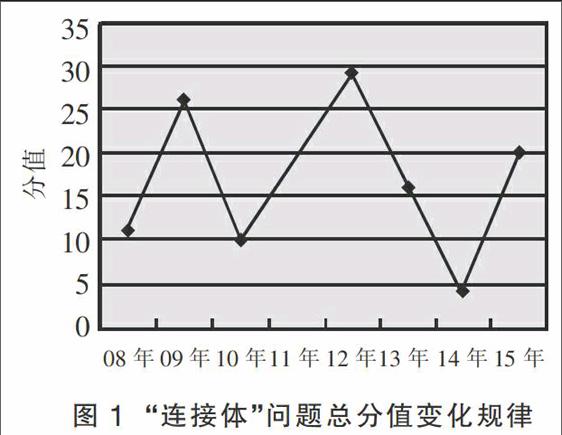
利用Excel软件生成历年总分值变化规律图，如图1所示。由该图可知，该类问题在江苏卷中的分值比重成周期性波动。

1.2    对象模型和运动模型的统计

在考查的试题中，就对象模型的取材而言，大致可分为三类：一类以高中阶段常见的模型为例（如，“车板模型”），适度变迁，考查学生的分析、评估、构建能力;一类取材于生活生产（如，“夹子夹木块”问题），很好地体现了物理来源于生活、应用于生活的思想，考查考生应用已有知识处理实际问题的能力;一类是新情景问题（如，“轻质绸带+木块”问题），考查学生的对象选择、类比建模、空间想象能力等。

就试题涉及的运动而言，在16道高考试题中，共涉及了11次单向直线运动、2次往复直线运动、1次平抛运动、2次圆周运动。由此可知，单向直线运动仍然是重点考查的运动模型。

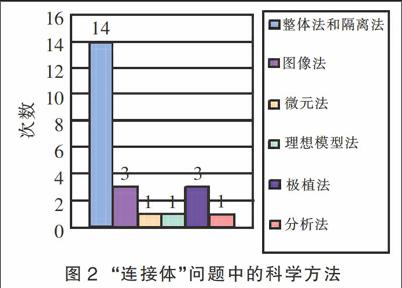
1.3    物理方法和处理观点的统计

“能力立意”是现行高考命题的主旋律[1]，在众多的高考试题中，突出了方法和思想的考查。在8年的“连接体”问题中，主要涉及6种方法的考查，如图2所示。可知“整体法和隔离法”几乎是每年的必考点，这也提示我们，在教学中应重视这类方法的渗透，“图像法”和“极值法”也应得到重视。

在考题中，主要涉及的处理方法为“力的观点”和“功能观点”。所谓“力的观点”是指以“牛顿第二定律”为中心，展开分析、解答;所谓“功能观点”是指利用“功能关系”或“能量守恒定律”解答。各类原理在历年试题中运用的比例如图3所示。由此可知，单一的“运用运动学公式求解”出现的比率最小，其他两种处理方法是主要的考查点。

2    教学策略

由于“连接体”问题的高频考查，为了能更好地应对这类问题，各学校在实际的教学中也有所侧重。但是，在实际教学中发现，学生对该类问题的掌握程度常常与我们教师的期望相去甚远。笔者曾在学科组其他老师的帮助下，对本校高三学生在“连接体问题”上存在的错误原因进行了归类分析：

①该类问题综合性强、涉及的知识点和方法较多，但是，学生实际学习中往往又存在薄弱点，学生难以完整、准确地求解;

②该类题型阅读量大，受题目文字表述的干扰，学生难以快速提炼题目要点、构建合理模型;

③该类问题过程较为复杂、运算量较大，耗时长，学生没有足够的耐心和信心来解答该题，甚至从心理上排斥这类试题。

针对上述分析，笔者认为要突破这一高频考点、学生学习中的难点，在二轮复习阶段可以从三个方面入手。

2.1    巧设问题，让学生在“慢教学”中提升理性认识

受一轮复习的进度、考试安排所限，教师在复习该块内容时，往往会讲授过多，但是，学生并没有很好地注入自身情感和经历自己的思维过程[2]，导致“学的程度”没有到位。因此，在二轮复习阶段，提倡“慢教学”，更多关注学生思维能力的深化和升华。具体做法是：依托例题设计问题串，在“思—说—画—算”的过程中，调动学生的思维，增加学生的思维量，提升学生分析问题的能力。

例题  如图4所示，一个长度为L=1 m、高度为h=0.8 m的长木板静止在水平地面上，其质量M=0.4 kg，一个质量m=0.1 kg的小物块（可视为质点）放置在其上表面的最右端。所有接触面间的动摩擦因数均为μ=0.5。设最大静摩擦力等于滑动摩擦力。现给长木板施加一个水平向右持续作用的外力。

求：

1）若F恒为4 N，试求长木板的加速度;

2）若F=kt，k>0，在t=0时刻到物体刚滑落这段时间内，试定性画出物块与长木板间摩擦力大小随时间变化的图像。

针对这一例题的分析，可以设计以下几个小问来展开教学。

步骤一，将两问糅合，将两个物体的运动情况按时间的顺序展开：①若拉力F=kt，思考该问题的三类情景，如，“F很小时，两者都静止”，“F较大时，两者一起向右加速”和“F达到一定值时，两者分离，以不同加速度向右加速运动”;②请同学们在草稿纸上画出三类情景中，M和m的各自受力情况并相互检查，最后，教师利用投影仪投影学生的习作并请学生分析。

步骤二，在对M和m可能的运动情景已有清晰的认识的前提下，直面学生在解答过程中出现的几个典型错误提出质疑：①题目要求木板的加速度，能否认为两者就是一定已经分离的？②M和m发生相对滑动的临界条件是什么？③要使M和m发生相对滑动，是不是只需要克服两个摩擦力就行了？

立足于学生的思维障碍处，以“问题串”的形式，帮助学生搭建思维上的“脚手架”，在学生的积极参与下，将该类问题中学生常见的错误化解于无形中，在一定程度上也引领学生加深对问题的认识，发展其分析、综合等能力。

2.2    利用实验，让学生在体验中增加感性认识

在课堂中适度融入体验，不仅可以帮助学生个体形成对知识、规律的认可、理解，还能引起学生心灵的震撼，激发对意义的深刻领悟[3]。例如，在上文例题的理性分析后，我们还可利用身边物品设计小实验，增加学生的感性认识：

①将两本书叠放（注意接触面不能太光滑），用一个力拉住下面的物块，拉力从零开始逐渐变大，由此可以观测两个物体的实际状态和相对运动情景;

②将两本书叠放在桌上，用两个弹簧秤分别勾住上下两本书，左边的不用力，右边的施加逐渐变大的拉力，从而感知，在M对地运动前，M和m间是不存在摩擦力的。

或者也可以教师预先做好实验，同时拍摄视频。在关键处，如物块和木板分离条件的演示用软件处理，变成慢镜头演示，这样通过演示和体验，让学生从“接受经验”过渡为“个体体验”，在获得第一手资料、信息的同时，加深对问题的感性认识。

2.3    归类训练，让学生在实战中提升分析能力

由上述考情分析可知，“连接体”问题常考、常新但又不失基础，针对这一点，我们可以在二轮复习中，安排相应专题，或是按连接的方式，或是按运动情景的不同，或是按所用物理方法等，进行归类。但是，题量要适当少些，留给学生足够的分析、思考的时间，从而在一定程度上消除学生畏惧这类题型的不良情绪。

在分析试题的过程中，尽量引导学生自行归纳出解决该类试题的通法，即“一象二图三类式”：

①“一象”是指处理这类问题时，首先应确立研究对象（整体法或隔离法），对象选择得好，往往可以将问题化繁为简，化难为易。当然，这两种方法并不是对立的，一般问题的求解中，应把这两种方法有机地结合起来，灵活运用。

②“二图”是指要作好两张图，即受力图和运动草图，这样既可以使问题的分析更符合实际情况，又可以“显化”多个物体的复杂空间关系，从而简化解答。

③“三类式”是指寻找未知量与已知量之间的关系，选择适当的物理规律列方程来求解。

参考文献：

[1]潘华君.白玉微有暇 表述须简洁——对2013年一道高考试题文本表述的探讨[J].物理教学探讨，2014，32（3）：39，42.

[2]潘华君，赵乃虎.“说题”模式在高三物理习题教学中的应用[J].中学物理教学参考，2014，46（6）：49—50.

[3]孙俊三.从经验的积累到生命的体验——论教学过程审美模式的构建[J].教育研究，2001（2）：34—38.

（栏目编辑  赵保钢）