对布依族民族数学教学案例编写的思考——以黔西南布依族苗族自治州为例

孙 健

（兴义民族师范学院， 贵州 兴义 562400）

对布依族民族数学教学案例编写的思考
——以黔西南布依族苗族自治州为例

孙 健

（兴义民族师范学院， 贵州 兴义 562400）

挖掘整理布依族传统文化中的数学文化，提炼蕴含其中的与数学教学相关的元素，编撰布依族民族数学教学案例，并将其运用于日常课堂教学，是解决布依族学生“文化偏向”问题、提高他们数学学习水平的一种重要方法。案例要精心选取素材，重点探索布依数学文化载体与现行数学教材的结合，多角度呈现数学情景并解决相关问题。

布依族；民族数学；教学案例

一、问题提出

我国是一个拥有56个民族的多民族国家，每个民族都有自己独特的民族文化。数学作为一种文化，和文学、艺术、宗教、哲学等文化一样，蕴含在丰富的民族文化当中。吕传汉先生在其关于民族数学文化与数学教育的论述中，对民族数学文化作出如下界定：民族数学文化可以理解为存在于民族文化群落里的数学思维模式及其系统实践的知识综合。

目前，“民族数学文化”的研究主要分为两大类：一类着重研究和重建那些在现代文明扩张过程中受压制和排斥的具有民族特色的数学知识、技能和思维方式；另一类则重点关注与学校数学教育直接相关的问题，认为民族数学文化的意义更主要在于它的现实作用和教育价值，教育工作者必须思考如何将民族数学文化与数学教学结合起来。

黔西南州是一个文化经济都欠发达的地区，布依族作为本地区的主体少数民族，主要居住在偏远的农村。根据调查得知，布依族学生一入学就面临“文化偏向”问题。由于国家统编教材对内容的限定性（文化背景多选取主流地区，与边远民族地区文化缺少关联），学生在课本中学到的内容与实际生活中接触到的本民族的东西有较大差异，造成他们数学学习困难，导致数学成绩普遍较差。要改变这一状况，最有效的工作就是研究布依族文化中的数学文化背景，开发和编写一些具有传统布依族文化特点，贴近学生实际，符合学生“最近发展区”的数学教学案例，作为通用数学教材的补充和参考。

二、案例素材的来源

布依族在长期的生产生活中，形成了特有的数学文化，主要表现在语言、建筑、服饰、生活用具等方面。所反映的数或形的数学知识，主要是对实体的再现，不一定具有系统性和规范性。所以，在编写教学案例时，要根据不同的教学功能取向，重点探索原生态布依数学文化载体与现行数学教材的结合，找到那些密切联系生活、符合数学基本形式特点的元素，结合“数学情境与提出问题”的教学模式进行编写。

图1

案例要以布依族生活中的“日常数学”作为出发点，应具有民族性和地域性，素材的选择可从几个方面去思考。

1．生动有趣的故事、民谣

对于刚接触数字运算的学生来说，可以借助一些故事、民谣来辅助记忆。《太阳瓜》是在布依族中流传很广的民间故事，其中有许多与乘法口诀相关的表述，通过加工整理，可以作为案例素材用于小学生乘法口诀教学。“太阳瓜，太阳瓜，苦兄弟去种它。他们划了八九七十二天的船，过了七七四十九个弯，翻了六六三十六个坳来到太阳山。犁了二九一十八陇地，挑了九九八十一挑红河水，又抬了八八六十四筐金鸡粪，日夜守望，经过三七二十一年，太阳瓜熟了，苦兄弟从此过上幸福生活”。

2．美丽多姿的服饰

布依族传统的手工织锦，本族人称之为“土布”，以它为材料制成的服饰是布依文化的重要载体。“土布”的剌绣纹样中有丰富的几何形状，包括正方形、三角形、菱形、多边形、圆形（弧）、扇形等，还有由上述图样进行变换得到的连续图样。利用这些服饰图案，可以编写认识图形、图形对称、图形变换、图形密铺、比例等教学案例。

图1是黔西南州常见的几种布依族服饰；图2至图8分别是服饰上的装饰图案，纹样有菱形、正方形、圆（弧）形、平行线、相交线、垂线等，有独立纹样（如图 2，3，4），也有由独立纹样多重复制或进行几何变换得到的连续纹样（如图5，6，7，8）。

图2

图3

图5

图7

3.独具特色的建筑

黔西南传统的布依族民居以小青瓦木结构的吊脚楼为主，楼房上悬下空，形成图9所示（在建）的“干栏式”建筑。它的建造技艺还被列入黔西南州第三批“非物质文化遗产名录”。在主体建筑和房屋装饰中，主要继承了我国古代木结构中的穿斗式结构，内部木构架节点是榫卯结合，不用一钉一铆。建造时会涉及到三角形、矩形、圆（弧）等形状，还会用到对称、比例、相似等多种数学关系，从中可以提取众多素材，设计认识图形、相似计算、三角计算、函数图象等案例。

图9

图4

图6

图8

图10

4.丰富多彩的生活用具

图11

布依族长期生活在边远山区，至今还保存着制作生活用具的传统工艺。有用竹子编制的筐、簸箕、桌椅，有手工雕刻拼接的窗户花格，还有手工制作的纺车、风斗等，其中蕴含着丰富的数学文化。图11的雕花窗图案精美，可让学生感受对称美和学习图形变换；图12的竹凳呈现圆与内接四边形的结构，可用于设计圆和内接四边形的认识和计算；图13的簸箕骨架是由几组平行竹条穿插构成，形成的多边形和三角形的图形排列有序，可用于设计认识图形密铺问题；图14的“升子”，图15的遮阳草帽和图16的木桶分别呈现了台体、锥体和柱体的形状，可作编写基本几何体的认识和计算的案例素材。

图12

图13

图14

图15

图16

三、案例编写的原则

布依族数学教学案例最终要应用于聚居区学生的课堂教学中，除了要有民族文化背景外，还须考虑编写的格式、目标的层次以及叙述的准确等问题。

1.统一性原则

案例的编写要有统一的格式模板。布依族数学教学案例编撰主要以“情境——问题”教学模式为依据，即“设置数学情境→提出数学问题→解决数学问题→数学应用”。根据这种教学模式，案例的编写可设计以下几个部分：“标题→知识点→数学情境→提出问题→解决问题→教学建议→附录（布依民族文化小知识等）”。

2.真实性原则

案例情境一定要真实反映布依族的民族文化内容，不能张冠李戴。在布依族聚居区，虽然有其他民族文化的融合，但仍保留着自己特有的民族文化特征，要寻找具有布依族特色的东西作为案例情境。比如以建筑为背景设计案例，应该是布依族的“干栏式”传统民居，而不是已经城市化了的砖混结构房屋。

3.层次性原则

案例的编写要有层次性。针对同一个情境，可以从不同的知识层面上去思考，不必太局限。如图17中的房屋装饰图，设计小学案例时，可从图形对称的角度去考虑；设计中学案例时，可建立直角坐标系，从曲线方程的角度考虑；在高等数学中，还可以从星形线的角度去考虑。

图17

4.恰当合理原则

情境与数学知识的结合要自然恰当。有的情境形式上可能与某个数学现象有些相近，但本质上经不起推敲，如把它用于教学，反而会对学生形成误导。在图18中，针对布依族服饰镶边上的波浪纹样，设计成对称或变换案例是可以的，但把它看作正（余）弦函数图象来设计案例就不适合了。

四、几个布依族数学教学案例分析

图18

【案例一】布依族手摇纺车中的正多边形。

【知识点】正多边形及相关计算。

【数学情境】布依族是一个心灵手巧的民族，到现在都还沿袭着手工织布的技艺，而手摇纺车就是必不可少的工具之一。这种纺车主要由木架、绳轮和手柄等几部分组成，其中绳轮是用等长木条均匀展开作为轮辐构成。根据绕线规格的不同，纺车可大可小，轮辐条数也可多可少，绕上纱线后，外形接近一个正多边形。图19是布依族传统的纺车，其外形为一个正十边形。

图19

图20

【提出问题】

假设图19中纺车的轮辐长为0.5米。

（1）它的中心角是多少度；

（2）求出该纺车旋转一圈所绕纱线的长度；

（3）求出该正十边形的面积。

【解决问题】

（1）如图20所示，它是一个正十边形，所以每个中心角都是36°。

（2）该正十边形可看作由十个全等的等腰三角形组成。任取三角形 OAB，则 OA=0.5，∠AOB=36°，OD是边心距。

∵AB=2AD=2×OA×sin18°=2×0.5×sin18°≈0.309（米）

∴周长=10AB ≈3.09米

所以，纺车旋转一圈所绕线长约为3.09米

（3）∵OD=OAcos18°=0.5×cos18°，AB=2×0.5×sin18°

∴S△OAB=≈0.0735（平方米）

所以，纺车面积S≈10×0.0735=0.735（平方米）。

注：计算中，sin18°和cos18°的值可查表求得。

【教学建议】

1.通过纺车的观察可知数学在生活中无处不在。

2.培养学生观察能力，使学生从熟悉的生活物件中提出数学问题，分析和解答问题，提高学生的学习兴趣。

3.让学生进行课外实践调查，收集关于布依族生产生活用具资料，从中获得布依族数学文化的初步印象。

【案例二】布依族铜鼓中的几何。

【知识点】圆的对称性和等分圆计算。

【数学情境】铜鼓，布依人称其为“布依神鼓”，它在布依族各种节日和祭祀活动中都是必不可少的。关于铜鼓的来历，有一个传说是这样的：从前，布依族老人过世后，不能上天成仙，只能下地转世。有一晚，太白仙人托梦给布依族祖先布杰说，要想族人上天成仙，必须向天神讨一面铜鼓。老人去世后就敲三声铜鼓，天神听到鼓声后，才会派仙人下凡将亡灵接引上天。布杰依仙人指点，历尽千辛万苦，终于求得一面铜鼓，使得布依族人去世后得以上天成仙。

图21是布依族铜鼓鼓面。它的纹饰可看着是由许多同心圆组成，中心圆内有一个八角形，图22是鼓面中心部分的平面图。

图21

图22

【提出问题】

（1）铜鼓是轴对称图形吗？如果是，有几条对称轴？

（2）铜鼓是中心对称图形吗？如果是，对称中心在哪里？

（3）在图22中，要将其面积四等分，可以怎样分割？

（4）设大圆的半径为OA=r，如果用与大圆同心的三个圆将大圆面积四等分，则这三个圆的半径OB,OC,OD各是多少？

【解决问题】

（1）铜鼓是轴对称图形，它有8条对称轴；

（2）铜鼓是中心对称图形，对称中心就是圆心；

（3）相互垂直的直径可将圆四等分，也可用同心圆来四等分一个圆；

（4）设三个圆的半径OB,OC,OD分别等于r1,r2,r3,由题意有

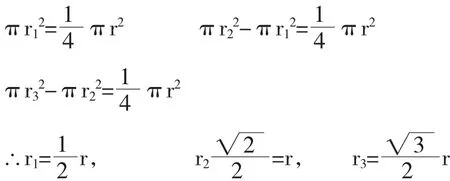
【教学建议】

学生通过对布依铜鼓的观察，认识圆的对称性，并能画出对称轴和知道对称中心。同时学会用不同的方法等分给定圆的面积，特别是用同心圆的方法来等分，是学生不一定能想到的，所以要重点引导。

【案例三】风斗中的直线和圆。

【知识点】圆和直线方程。

【数学情境】图23是布依族生活的一种生活用具，通常叫风斗。它是应用空气动力学的原理进行稻谷分类的传统工具。将稻谷从三角漏斗处倒入，转动风鼓（圆形部分）的扇叶，就可将稻谷中的饱满颗粒和瘪谷分离开。

从侧面可，它可看成是圆与直线相切。如图24建立坐标模型，假设该圆的圆心在坐标原点O，半径为4，△ABC的边AB与圆相切于D点，OB=5。

图23

图24

【提出问题】

（1）试求圆的标准方程；

（2）求直线AB的直线方程。

【解决问题】

（1）圆在坐标原点，其半径为4，所以该圆的标准方程为

x2+y2=16

（2）∵OB=5 ∴点B的坐标为（5，0）

设直线的斜率k，则所求直线方程为

kx-y-5k=0

∵AB与圆相切于D

∴直线AB的方程为4x+3y-20=0

【教学建议】

通过仔细观察风斗形状，形象直观地引出“直线和圆相切”的数学模型，结合“数形结合”的方法解决问题，一定能极大地激发学生的学习兴趣，更好地实现教学目标。

五、结语

编写布依族数学教学案例的目的，主要在于尊重和传承布依族传统文化，培养布依族学生的数学兴趣，突破学习障碍，提高数学成绩。此外，通过案例，对民族服饰、建筑及生活用具作出数学描述及解释，还能激发布依族学生对本民族文化探究的兴趣，达到从数学角度思考和欣赏布依族文化的目的。

[1]吕传汉，张洪林.民族数学文化与数学教育[J].数学教育学报，1992,1（1）：101-104.

[2]张维忠，唐恒钧.民族数学与数学课程改革[J].数学传播（台湾），2008，32（4）：80-90.

[3]罗永超，张和平，肖绍菊等.苗侗数学文化与数学情境教学[M].北京：民族出版社，2012.

[4]贺光澍.黔西南布依学研究[M].社会科学文献出版社，2013.

[5]周长军，申玉红，郭彩莲.民族数学文化与数学教育[M].浙江：浙江大学出版社，2014.

On Compilation of the Buyi National Mathematics Teaching Cases

SUN jan
(Xingyi Normal University for Nationalities, Xingyi,Guizhou 562400,China)

Through mining and organizing the mathematical culture of the Buyi traditional culture,refining contains elements relevant to the teaching of the mathematics,the compilation of Buyi Ethnic Group of mathematics teaching case for the daily classroom teaching,Buyi students"cultural bias"problem solving,improve their mathematics learning level of an important method.Cases must be carefully selected materials,focusing on exploring the combination of mathematical culture carrier in the Buyi and the current mathematics teaching materials,multi angle present mathematics situation and solve the related problems.

Buyi;National Mathematics;Teachingcases

1009—0673（2015）04—0072—08

G752

A

2015—07—31

贵州省科技厅联合基金重点项目“布依族数学文化的模型建立与教育研究”，项目编号为黔科合LH字【2014】7408号。

孙健（1971— ），男，贵州贞丰人，兴义民族师范学院数学科学学院副教授，研究方向：课程与教学论。

责任编辑：彭光明