基于MATLAB的鱼雷推进轴系弯曲振动涡动频率计算

赵　琪，尹韶平，王　中，郭　君

（1. 中国船舶重工集团公司 第705研究所，陕西 西安，710075； 2. 水下信息与控制重点实验室，陕西 西安，710075）

基于MATLAB的鱼雷推进轴系弯曲振动涡动频率计算

赵琪1，2，尹韶平1，2，王中1，2，郭君1

（1. 中国船舶重工集团公司 第705研究所，陕西 西安，710075； 2. 水下信息与控制重点实验室，陕西 西安，710075）

在鱼雷转子系统中，为避免系统发生共振，常需要计算其涡动频率。鉴于商业有限元分析软件的输入参数有限，且无法满足特殊情况下的计算需求，该文根据转子系统的运动微分方程及其求解过程，运用MATLAB软件编程来计算系统的涡动频率，然后与ANSYS软件计算结果进行对比。结果表明，所编写的MATLAB程序合理，可对鱼雷推进轴系进行计算，也可进行后续开发。

鱼雷推进轴系； 弯曲振动； 涡动频率

0　引言

一般工业中常见的机器都装有旋转部件即转子。 转子连同它的轴承和支座等统称为转子系统。转子系统的振动是多样的，包括转轴的纵向振动、扭转振动和弯曲振动等。其中转轴的弯曲振动较为复杂，牵扯的因素较多。该文就是以转轴的弯曲振动作为研究对象。

求解系统的涡动频率及临界转速，是转子动力学研究的重要内容之一［1］。当转子达到临界转速时，往往产生剧烈振动，为了避免这种现象，就必须计算转子的涡动速度。计算方法有传递矩阵法和有限元法等。采用有限元法建立的模型能考虑的因素比传递矩阵多，且数值稳定，计算精度较高，因此得到了非常广泛的应用。现在应用较多的有限元分析软件，如ANSYS，ABAQUS等，虽然都可以进行轴系振动特性分析，但其输入参数有限（如弹簧的刚度阻尼系数等），而实际情况又都较为复杂，存在弯、扭、纵的耦合振动，需要考虑更加全面的边界条件； 另一方面，当商业软件不能满足特定情况的计算需求时，要对其进行更多功能的开发较为困难。因此该文采用MATLAB编程计算和分析，实现对输入参数的控制，也为后续其他功能的实现打好基础。

1　有限元分析理论基础

1.1涡动频率

通常转轴的两支点在同一水平线上，中心线是水平的。当圆盘受横向力作用，圆盘或转轴的中心o′在互相垂直的2个方向作频率同为wn的简谐运动。一般情况下，中心o′的轨迹为一椭圆，如图1所示。o′的这种运动是一种“涡动”或称“进动”，自然频率wn称为涡动角速度［2］。

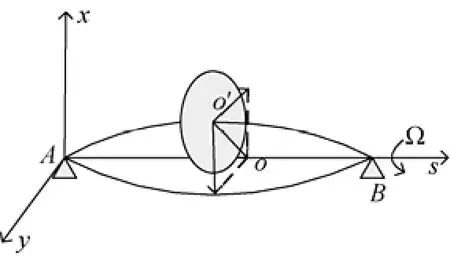
图1　转子涡动示意图Fig. 1　Schematic of rotor whirling

1.2运动微分方程

转子系统通常由刚性圆盘、弹性轴段和轴承座等部件组成，因此可沿轴线将转子系统划分为圆盘、轴段和轴承座等单元，各单元间彼此在结点处联结。结点通常选在圆盘中心、轴颈中心以及轴的变截面等位置。如以轴承座中心线为s轴建立坐标，则转子系统的具体结构见图2［3］。

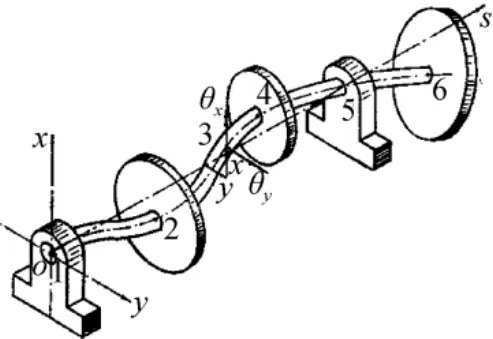
图2　转子系统结构Fig. 2 Structure of a rotor system

基于上述模型，建立转子系统运动微分方程

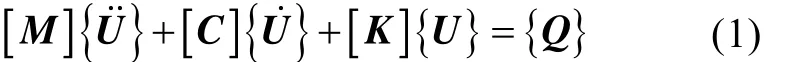
式中： ｛U｝，｛Q｝分别为系统位移向量及广义力；［M］，［C］和［K］分别为系统质量矩阵、回转矩阵和刚度矩阵。系统矩阵是由单元矩阵根据对应结点叠加而成的。

1.3结点为4自由度的单元矩阵形式

若考虑每个结点为4自由度状态，则任一截面的位移可表示为

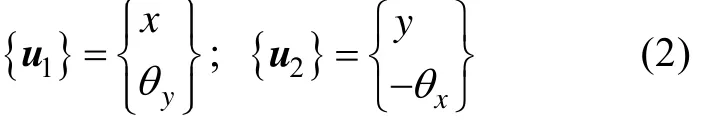
设刚性圆盘的质量、直径转动惯量和极转动惯量分别为m，Jd和Jp，则圆盘的质量矩阵［Md］和回转矩阵［Gd］为

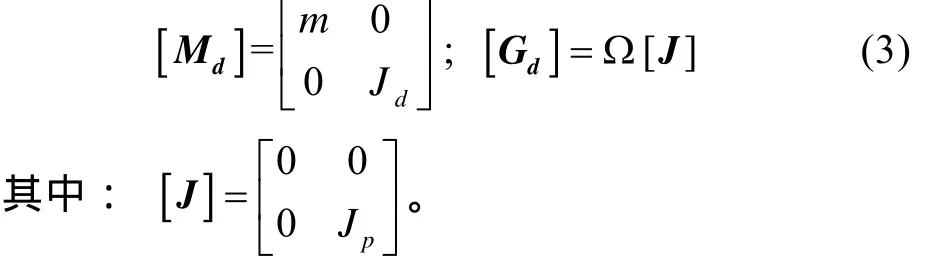
设轴段单元长度为l，半径为r，单位长度质量为μ。则其移动惯性矩阵［MsT］、转动惯性矩阵［MsR］和回转矩阵［Gs］分别为［4-5］

可得轴段单元的质量矩阵为

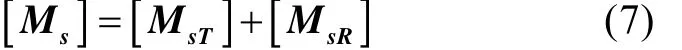
轴段单元刚度矩阵为

根据各单元间的相互作用关系，将单元矩阵进行集总，形成系统整体矩阵。

1.4结点为6自由度的单元矩阵形式

若考虑每个结点为6自由度状态，圆盘单元只有一个结点，其位移向量可表示为

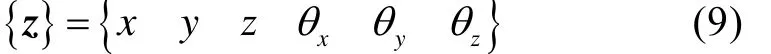
其质量矩阵及回转矩阵可表示为

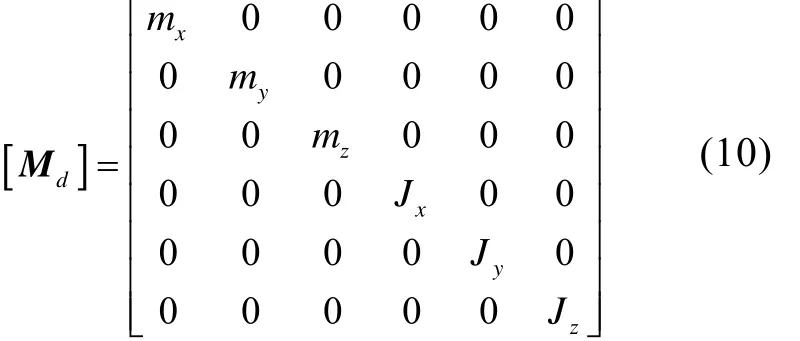
其中： mx，my和mz为质量单元3个方向的质量； Jx为极转动惯量； Jy，Jz为直径转动惯量。

轴段单元为两结点单元，每个结点均有6个自由度，其单元的刚度矩阵为［6］

式中： A为横截面面积； Ixx是横截面对x轴的极惯性矩； Iyy和Izz是单元截面对y和z轴的主惯性矩。

轴段单元的一致质量矩阵为［7-8］

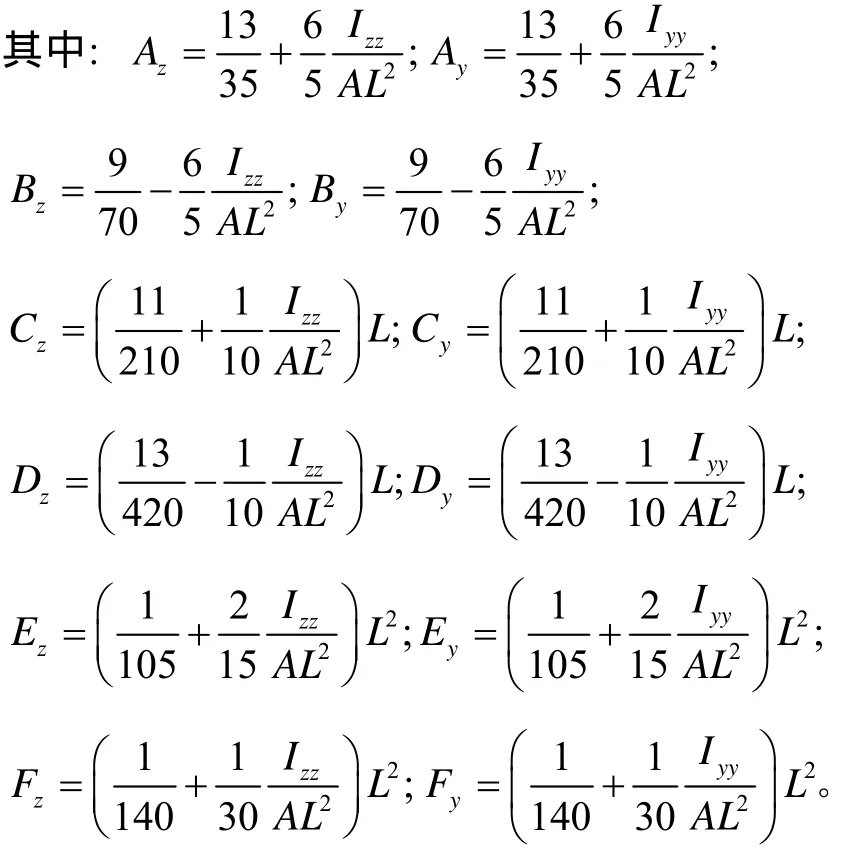
回转矩阵为

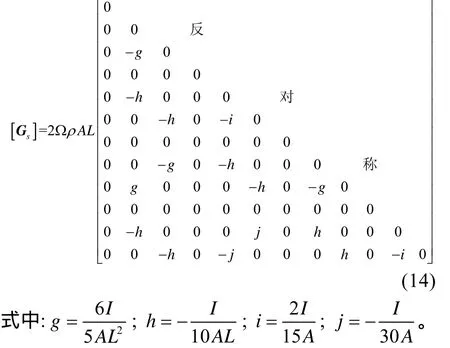
将上述单元矩阵叠加，即可得到系统矩阵。

2　运动微分方程的求解

系统运动微分方程的齐次式为

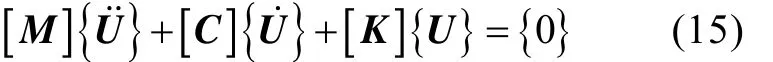
在结构动力学中，求解这种大型稀疏带状矩阵特征值问题的程序，通常要求在对称矩阵情况下使用。而在转子动力学中，由于轴承动力特性参数中包括交叉刚度和交叉阻尼，且二者往往并不相等，使得刚度矩阵［K］失去了对称性，因此一般采用复模态理论求解转子动力学方程。

复模态理论是将运动方程的齐次式化为1阶微分方程组来求解，即令

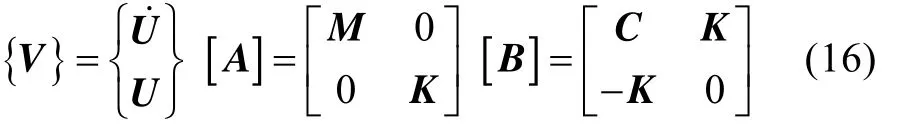
则运动方程的齐次式可改写为

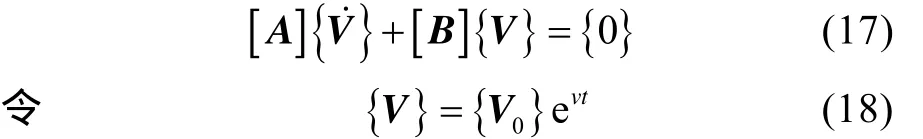
带入式（17）可得

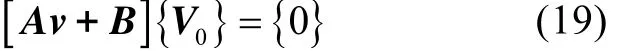
由此可求解特征值v及特征向量｛V0｝。特征值v即为系统在给定自转角速度下的涡动频率，且根据特征向量｛V0｝可得相应的模态振型。

3　MATLAB编程

3.1编程流程

根据上述对系统运动微分方程及其求解过程的分析，编写MATLAB程序。

首先对转子系统进行结点单元的划分，以建立有限元模型。其次计算结点处的单元矩阵，并将单元矩阵按照结点位置进行叠加，形成系统整体矩阵，得到微分方程中的矩阵参数。最后根据支承情况，对系统刚度矩阵进行修正处理。在求解过程中，根据复模态理论对系统矩阵进行扩充，将运动方程转化成1阶微分方程组，然后可直接利用MATLAB中eig程序（求特征值和特征向量）进行求解。

程序具体流程如图3所示。

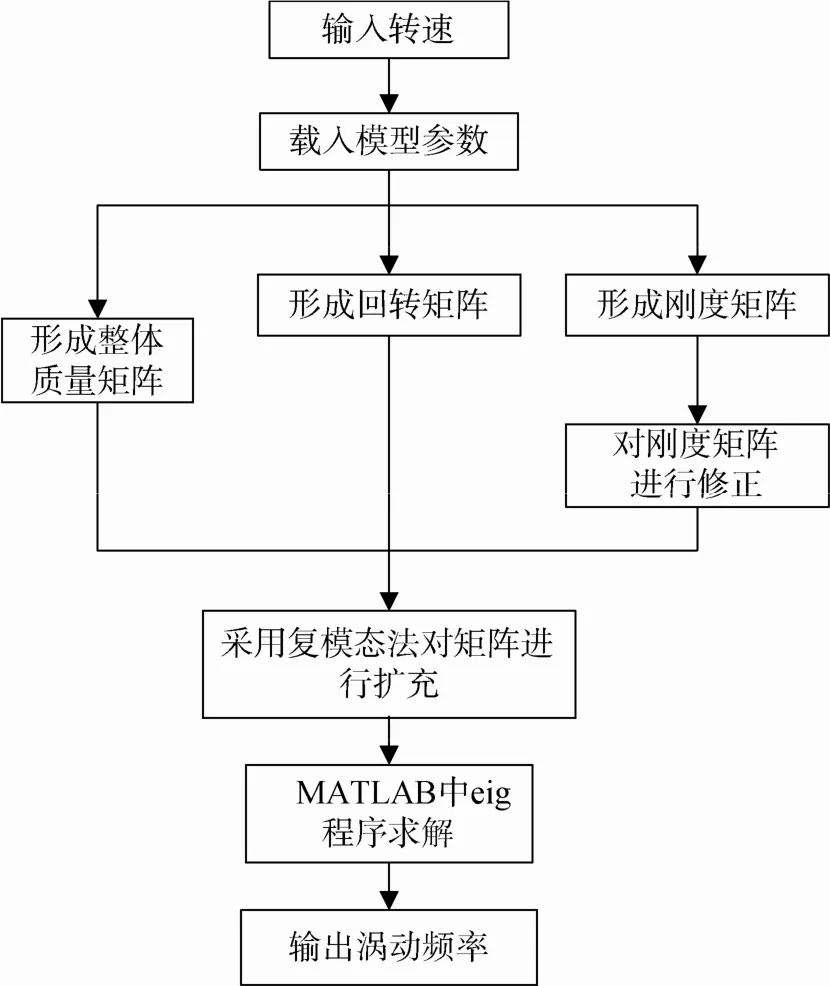
图3　编程流程图Fig. 3　Flowchart of programming

按照结点处为4自由度和6自由度状态分别编程。4自由度和6自由度程序的单元叠加方式一致，但在对刚度矩阵进行修正时会有所差异。

3.24自由度刚度矩阵修正

对于一般的轴承单元，其刚度、阻尼系数矩阵分别为

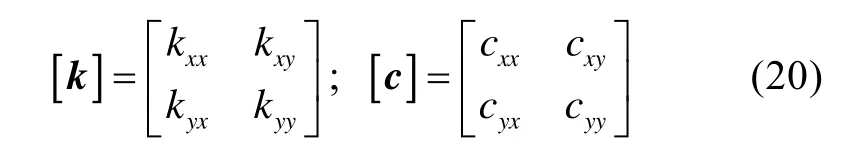
若假设系统具有N个结点，其间用N-1个轴段连接而成，则系统的位移向量由式（2）改写为

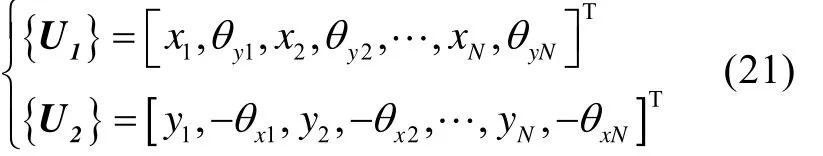
考虑支承处的轴承作用，则此时系统运动方程为

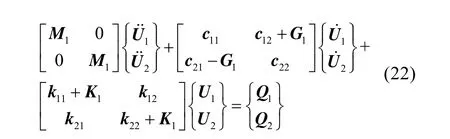
假设第j个结点为轴承单元，则在2N×2N阶的矩阵［c11］，［c21］，［c12］，［c22］和［k11］，［k12］，［k21］，［k22］中，除了第2s（j）-1行和2s（j）-1列中有元素cxx，cxy，cyx，cyy，kxx，kxy，kyx，kyy外，其余元素都为零。

则运动微分方程的各个参数为如下形式

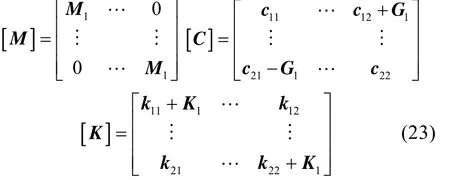
3.36自由度刚度矩阵修正

考虑轴承单元6个方向的连接刚度，则其刚度系数矩阵形式为

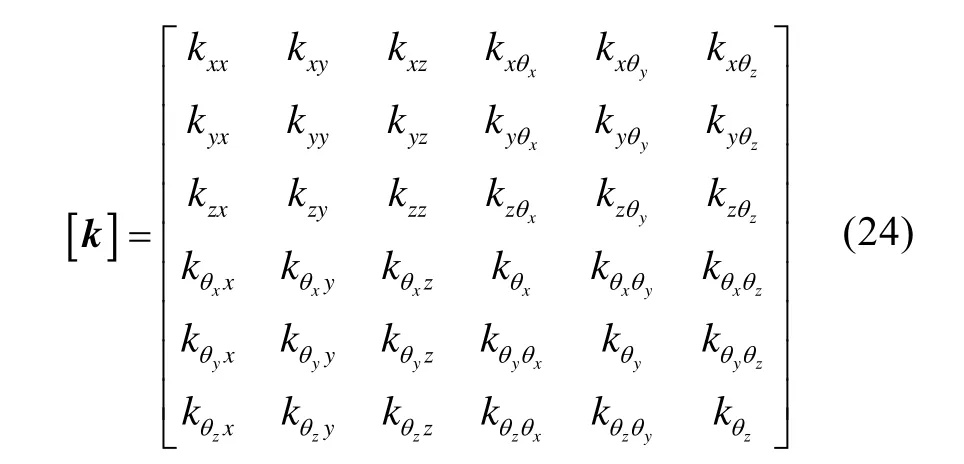
在对系统刚度矩阵进行修正时，可将轴承的刚度系数矩阵按照其结点位置直接叠加到系统矩阵中进行计算。

4　算例分析

ANSYS帮助文档中VM254算例［9］的模型为典型的转子动力学模型。它由刚性圆盘、变截面的弹性轴段及滑动轴承组成，具体结构见图4。在变截面处、支承位置和圆盘位置设置结点，则可沿轴线自左至右将轴段划分为18段，总计19个结点。模型具体参数可参考ANSYS帮助文档。

ANSYS运行结果的坎贝尔图如图5所示。图中交点的横坐标即为临界转速值。应用所编写的MATLAB程序对上述模型进行计算。按4自由度状态得出的坎贝尔图见图6。

按6自由度状态得出的坎贝尔图见图7。

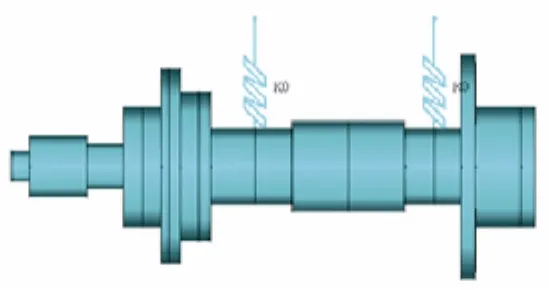
图4　转子模型Fig. 4　Rotor model

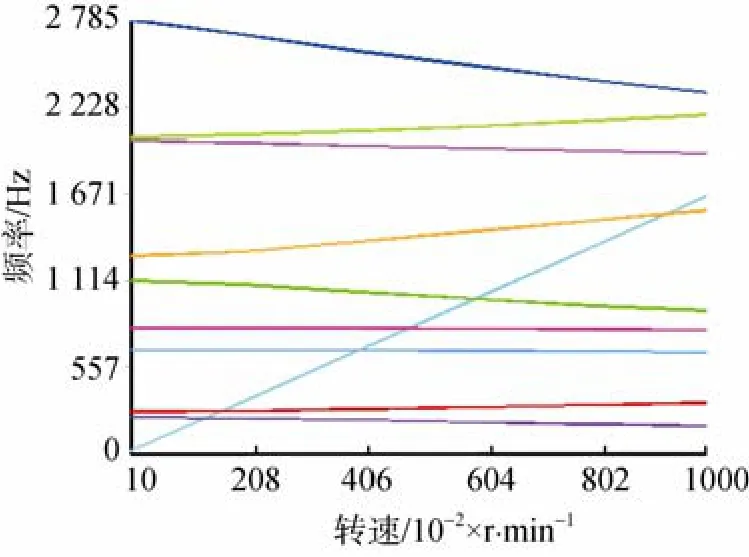
图5　ANSYS得出的坎贝尔图Fig. 5　Campbell diagram from ANSYS

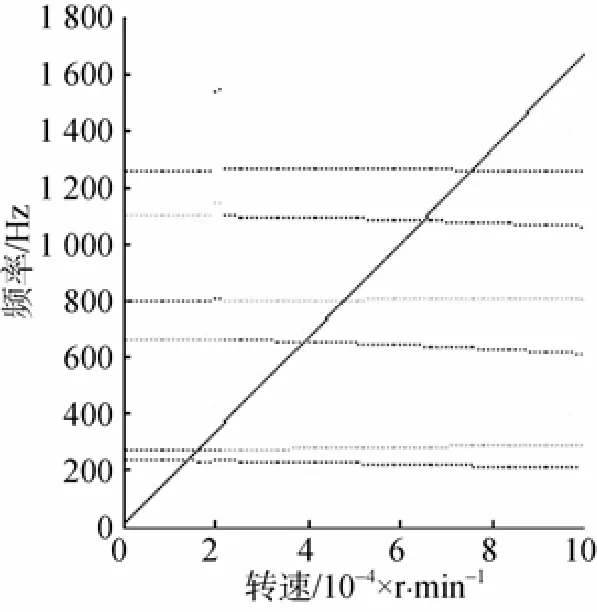
图7　6自由度状态的坎贝尔图Fig. 7　Campbell diagram of six-degree-of-freedom state

在输入转速为105r/min时的涡动频率计算结果如表1所示。

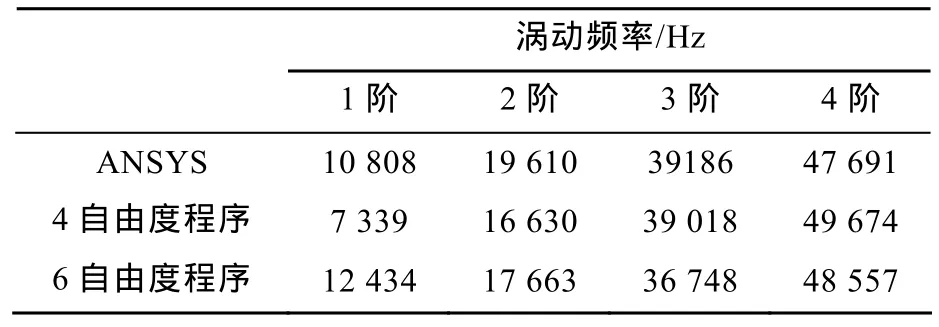
表1　涡动频率计算结果Table 1　Calculation results of whirling frequency

对比三者间的坎贝尔图可以看出，6自由度程序得出的结果与ANSYS比较吻合。通过分析在转速为105r/min时的计算结果可以看出，6自由度程序所得结果较4自由度程序更接近ANSYS的计算结果。所以，可以认为6自由度程序是合理的，可以用来计算鱼雷推进轴系的涡动频率。

5　6自由度程序在鱼雷推进轴系的应用

5.1鱼雷推进轴系结构及其有限元模型

鱼雷推进轴系结构如图8所示。动力装置与花键轴之间、花键轴与尾轴之间通过花键相连，推进器转子安装在尾轴上。花键轴及尾轴主要用于将动力装置的输出功率传递给推进器，而推进器工作时产生的推力通过推力轴承传递至雷尾壳体，推动鱼雷航行。在花键轴与尾轴相连的一端装有弹性花键套（图中标记2）。尾轴的支撑是靠隔板的滚珠轴承和尾盖处的滑动轴承，在滚珠轴承及滑动轴承外侧都安装了金属橡胶隔振器（图中标记5和9）。

鱼雷推进轴系简化模型（将推进器作为质量单元处理）如图9所示。

建立鱼雷推进轴系的有限元模型，可以沿轴线将花键轴和尾轴划分为若干个结点，如图10所示。对于弹性花键套，可以采用等效轴段法模拟其横向刚度和转角刚度。图中，结点1为花键轴前端，与动力装置相连； 结点2为花键套简化位置； 结点8，9和10为弹性花键套简化位置； 结点11和19为轴承支撑位置； 结点21为推进器安装位置。

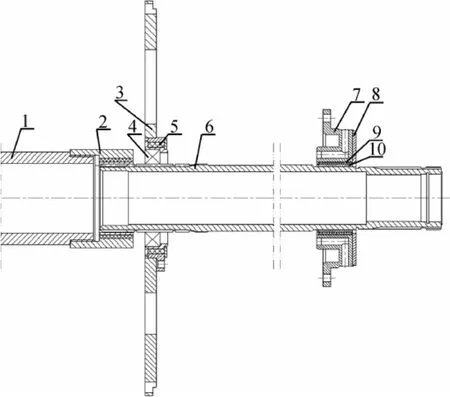
图8　鱼雷推进轴系结构Fig. 8　Structure of torpedo propulsion shafting

图9　推进轴系简化模型Fig. 9　Simplified model of torpedo propulsion shafting

图10　花键轴和尾轴的结点划分Fig. 10　Elements dividing of spline-shaft and tail-shaft

5.2计算结果与分析

应用6自由度MATLAB程序对鱼雷推进轴系进行涡动频率计算，得出的坎贝尔图见图11。

选取转速1150 r/min，1500 r/min和2050 r/min时的前4阶涡动频率如表2所示。利用ANSYS软件进行计算的结果见表3。对比推进轴系不同转速下的前4阶涡动频率可得，MATLAB程序计算结果与ANSYS计算结果基本一致，证明该文所编程序是合理的。

6　结束语

根据转子系统的运动微分方程，从2个方面进行编程，分别计算了结点为4自由度状态和6自由度状态时的结果。6自由度状态考虑了结点在3个方向的位移和转角，并在进行系统刚度矩阵修正时，对轴承刚度和阻尼系数的处理方式也比较完整，更接近于实际情况。

基于此程序，可以对转子系统在其他实际状态下进行涡动频率及临界转速等因素的分析，也可进行后续的开发。

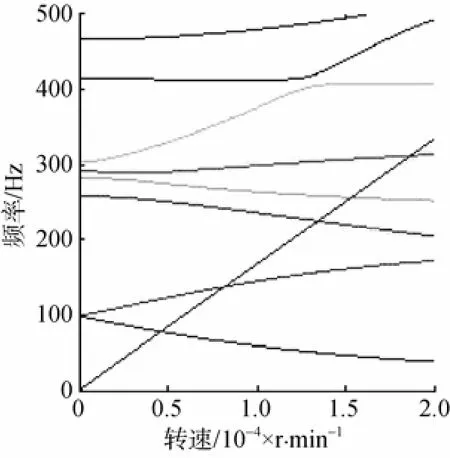
图11　推进轴系坎贝尔图Fig. 11　Campbell diagram of propulsion shafting

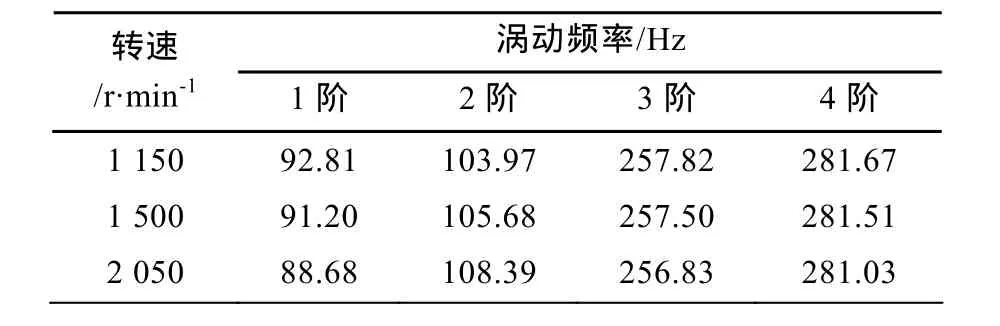
表2　MATLAB计算结果Table 2　Calculation results of MATLAB

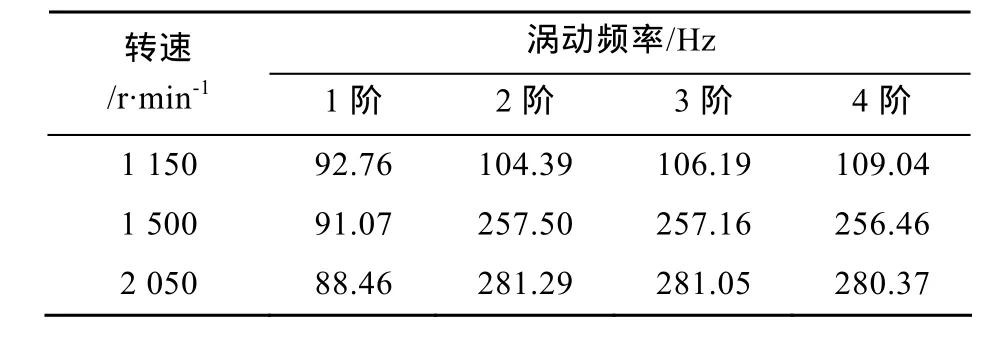
表3　ANSYS计算结果Table 3　Calculation results of ANSYS

［1］阮小丽. 基于传递矩阵法和有限元法的转子动力学分析［J］. 机电工程技术，2011，40（3）： 71-73.

Ruan Xiao-li. Based on Transfer Matrix Method and the Finite Element Method Analysis of Rotor Dynamics［J］. Mechanical & Electrical Engineering Technology. 2011，40（3）： 71-73.

［2］钟一谔. 转子动力学［M］. 北京： 清华大学出版社，1984.

［3］王军峰，孙康. 基于有限元法的转子临界转速计算［J］.机械设计. 2012，29（12）： 10-13.

Wang Jun-feng，Sun Kang. Rotor Critical Speed Calculation Based on Finite Element Method［J］. Journal of Machine Design.2012，29（12）： 10-13.

［4］汪梦甫，王朝晖. 两种质量矩阵在梁模态分析中差异的比较［J］. 地震工程与工程振动. 2006，26（6）： 84-86.

Wang Meng-fu，Wang Zhao-hui. Analysis of Differences Between Two Types of Mass Matrixes in Beam Modal Analysis［J］. Earthquake Engineering and Engineering Vibration. 2006，26（6）： 84-86.

［5］徐荣桥. 结构分析的有限元法与MATLAB程序设计［M］. 北京： 人民交通出版社，2005.

［6］车树汶，陈权，楼松庆. 质量矩阵模式对桥梁自振频率的影响［J］. 兰州交通大学学报，2003，22（6）： 80-83.

Che Shu-wen，Chen Quan，Lou Song-qing. Influence of Mass Matrix Model on Natural Vibration Frequency of Bridges［J］. Journal of Lanzhou Jiaotong University，2003，22（6）： 80-83.

［7］董军，刘旭红，姚顺忠，等. 基于虚功原理表达的空间梁单元刚度矩阵分析［J］. 西南林学院学报，2002，22（4）：59-62.

Dong Jun，Liu Xu-hong，Yao Shun-zhong，et al. Analysis of Element Stiffness Matrix About Space Beam-Element Based on Principle of Virtual Work［J］. Journal of Southwest Forestry College，2002，22（4）： 59-62.

［8］王勖成. 有限单元法［M］. 北京： 清华大学出版社，2003.

［9］Vaugh N M. The Dynamics of Rotor-Bearing Systems Using Finite Element［J］. Journal of Engineering for Industry，1976，98（2）：593-600.

（责任编辑： 陈曦）

Calculation of Whirling Frequency in Flexural Vibration of Torpedo Propulsion Shafting Based on MATLAB

ZHAO Qi1，2，YIN Shao-ping1，2，WANG Zhong1，2，GUO Jun1
（1. The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China； 2. Science and Technology on Underwater Information and Control Laboratory，Xi′an 710075，China）

To avoid resonance，it is necessary to calculate whirling frequency of a rotor system. The input parameters of commercial finite element analysis（FEA）softwares are limited，and these softwares can not complete the analysis of special cases. In this paper，according to the differential equation of motion for a rotor system and its solution process，a program is coded to calculate the whirling frequency by the software MATLAB. Comparison between the results of MATLAB and ANSYS shows that this MATLAB program is reasonable，and it can be used to calculate whirling frequency in flexural vibration of torpedo propulsion shafting or to perform subsequent development.

torpedo propulsion shafting； flexural vibration； whirling frequency

TJ630.1

A

1673-1948（2015）01-0007-07

2014-05-14；

2014-07-10.

赵琪（1989-），男，在读硕士，研究方向为鱼雷总体技术.