基于时频分析的水声目标被动检测模型研究

严　侃，雷江涛

（海装西安局，陕西 西安，710054）

基于时频分析的水声目标被动检测模型研究

严侃，雷江涛

（海装西安局，陕西 西安，710054）

为了获取复杂环境中瞬态或非平稳水声信号的特征和高检测概率，提出了一种基于时频分析和统计模型的水声目标被动检测方法，建立了基于短时傅里叶变换、Wigner-Ville分布和小波变换这3种时频分析方法的被动检测模型。结合实测的舰船辐射噪声数据进行目标检测与分析，结果表明，尽管这3种时频分析方法都能有效地将目标检测出来，但是基于小波变换的被动检测模型的检测性能最好。

时频分析； 水声信号； 目标检测

0　引言

在复杂的海洋水声环境中进行目标检测时，如何获得高检测概率一直是研究难题之一。为了获得高检测概率和作用距离，人们研究了许多方法，如目标运动特征和瞬态信号特征分析等。由于目标的运动状态变化往往很突然，表征其状态的瞬态信号的持续时间都很短。而传统的信号处理方法都是基于信号和噪声是线性平稳性的高斯随机过程这一假设的，因此利用基于Fourier变换的传统信号处理方法很难准确获取这些水中目标的瞬态或非平稳的辐射噪声特征［1］。

时频分析方法可以从时域和频率这2个不同的角度对信号进行观察和表征，它们展开过程中固有的局部化特性使它特别适合于描述瞬态信号。例如，在实际应用中，可选择基于短时傅里叶变换（short-time Fourier transform，STFT）［1］、Wigner-Ville分布［2］和小波变换［3］等现代信号处理的时频分析方法，以与瞬态水声信号的非对称及突变特性相适应。利用时频方法展开后，得到观测信号的时频分析展开系数后，就可以用其系数来检测瞬态的水声信号目标是否存在了。

基于STFT、Wigner-Ville分布和小波变换等时频分析方法和能量检测方法，文中提出了一种基于时频分析的水声目标被动检测模型。结合实测数据分析，验证了该方法的有效性。

1　基于时频分析的被动检测模型

对二元检测问题中的传统辨别式两边求时频分析展开系数，得

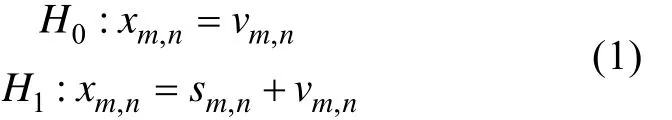
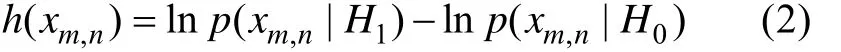
在检测过程中，选定判决准则（如Neyman-Pearson准则）［4］就可进行信号检测了。由此可以定义时频分析被动检测模型的判别式为

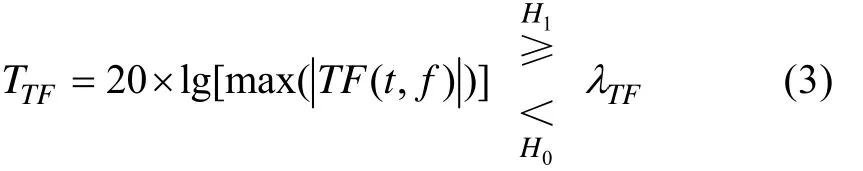
式中： TTF为检验统计量； λTF为检验门限。

实际应用该判别式时，为了充分利用时频信息，将时频面划分为N×N等份，取N2个最大时频能量的平均值作为检测统计量。时频面划分的示意图如图1所示。

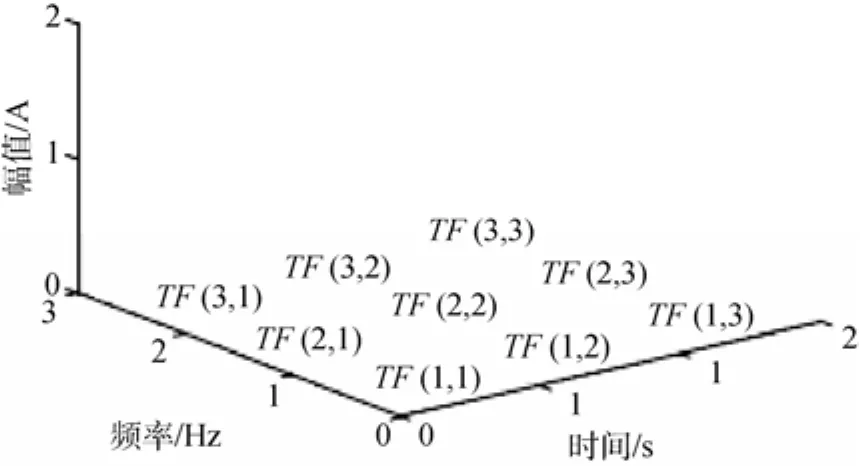
图1　时频面划分示意图Fig. 1　Schematic of dividing time-frequency plane

如示意图所示，取N=3，沿时间轴和频率轴将时频面划分为3×3个等份TF（i，j），（i，j=1，2，3）。此时的时频分析被动检测模型的判别式为［5］

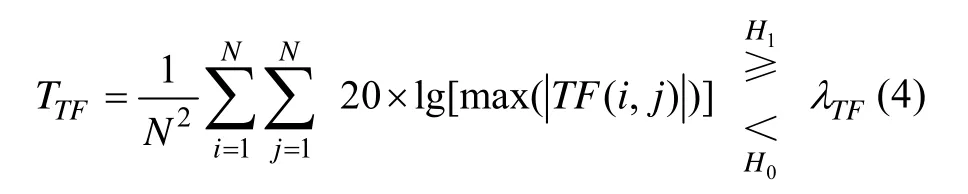
2　仿真和实测数据的目标检测分析

2.1仿真分析

下面利用一个仿真信号对基于时频分析的被动检测模型进行说明。设观测信号

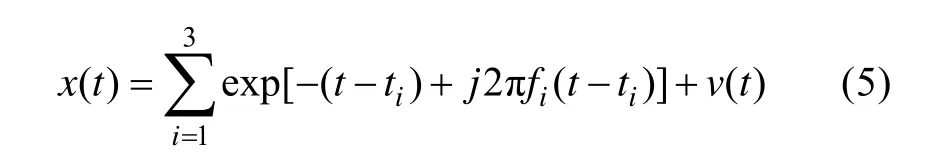
式中： 目标由3个不同瞬时信号叠加而成； t1，t2，t3分别为10 s，10 s，35 s； f1，f2，f3分别为5.5 Hz，7.5 Hz，5.5 Hz； v（t）为高斯白噪声。

设定信噪比SNR为5 dB，仿真信号的波形如图2所示。

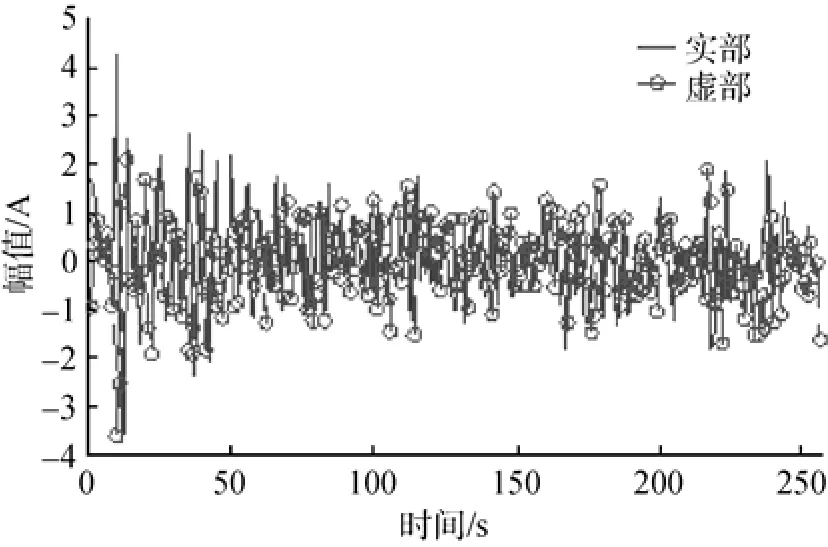
图2　仿真信号波形Fig. 2　Waveform of simulation signal

仿真信号经过基于STFT变换、Wigner- Ville分布和小波变换后的时频谱分别见图3～图5。

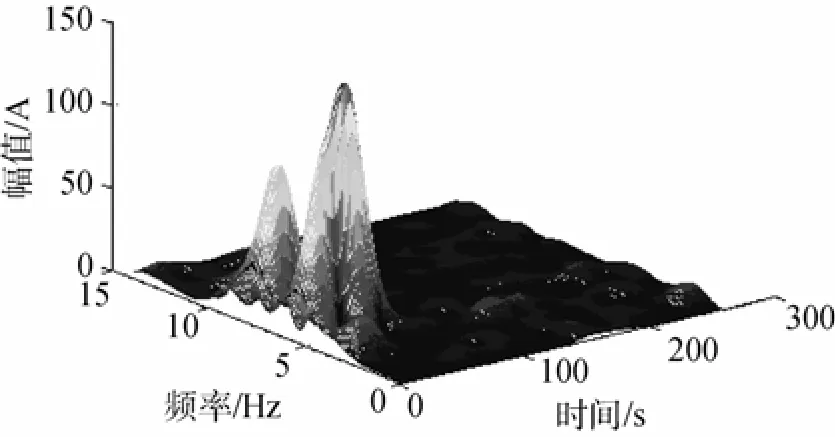
图3　基于短时傅里叶(STFT)变换的仿真信号时频检测Fig. 3　Result of time-frequency detection of simulation signal based on short time Fourier transform (STFT)

可以看出，这3种时频分析方法的时频图不仅可以将瞬时信号的频率和时刻检测出来，而且在目标检测时，可以根据统计设定1个检测门限λ，从噪声背景中将目标检测的峰值检测出来，从而达到实现目标检测的目的。

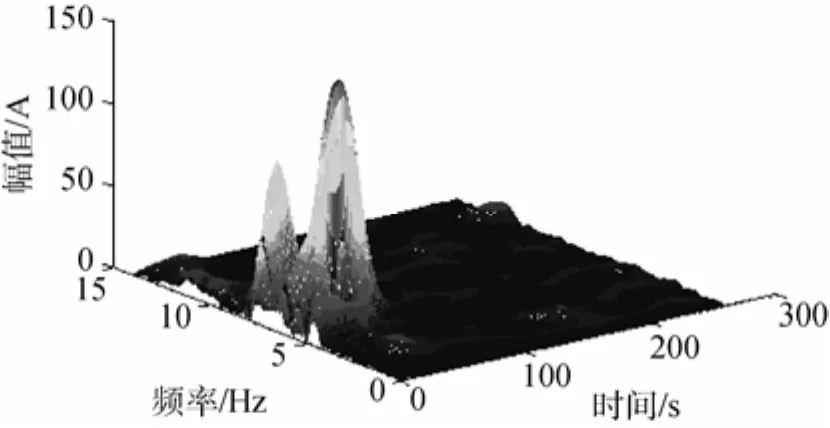
图4　基于Wigner-Ville分布的仿真信号时频检测Fig. 4　Result of time-frequency detection of simulation signal based on Wigner-Ville distribution

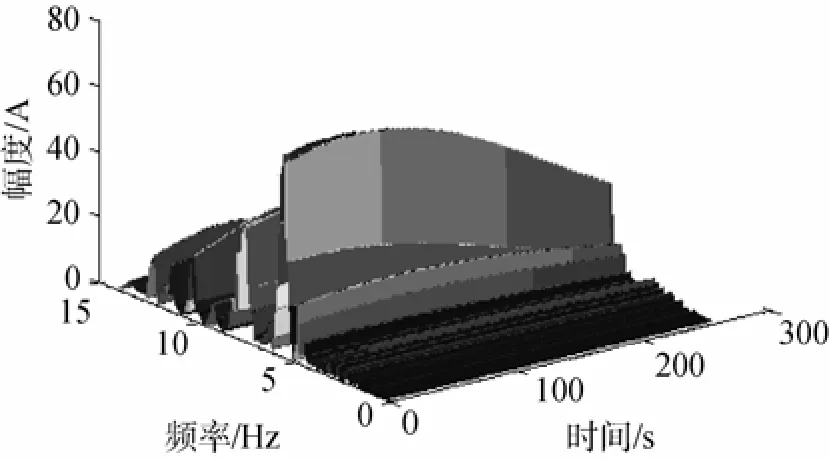
图5　基于Morlet小波变换的仿真信号时频检测Fig. 5　Result of time-frequency detection of simulation signal based on Morlet wavelet transform

2.2实测数据分析

利用基于时频分析的被动检测方法对某一实测的舰船辐射噪声进行检测分析，采样频率为Fs=6kHz，采样时间为85.3 ms，它的时域波形及其频谱如图6所示。

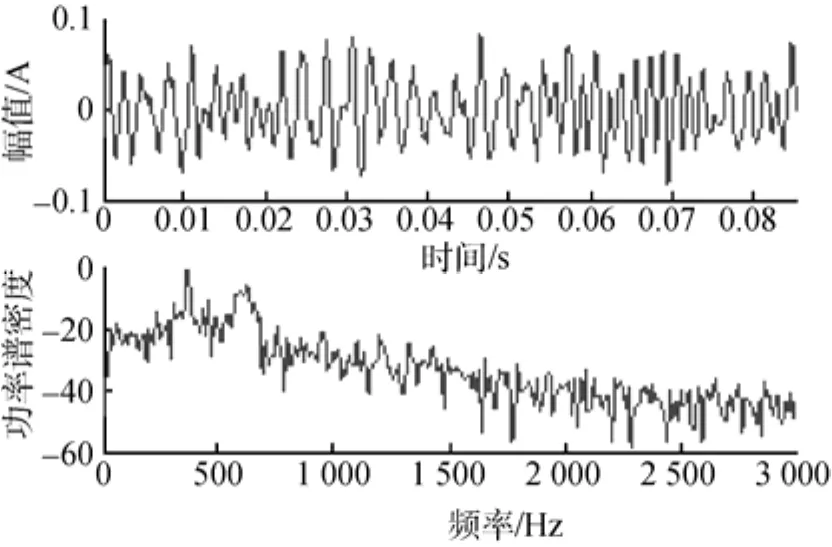
图6　舰船辐射噪声波形及其功率谱Fig. 6　Waveform and power spectrum of ship-radiated noise

图6中的舰船辐射噪声信号经过基于STFT、Wigner-Ville分布和小波变换后的时频谱分别如图7～图9所示。

从图7～图9中可以看出，这3种基于时频分析的检测方法都可以将辐射噪声中的特征频分量提取出来，特别是基于Morlet小波变换的时频检测方法提取出的2个低频分量明显可辨，这说明它的频率分辨率更高，具有较好的检测性能。

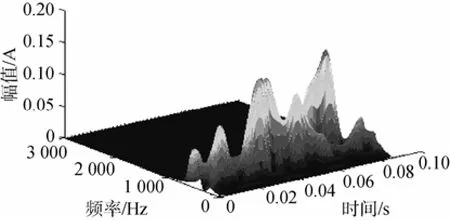
图7　基于STFT的实测噪声时频检测Fig. 7　Result of time-frequency detection of measured noise based on STFT

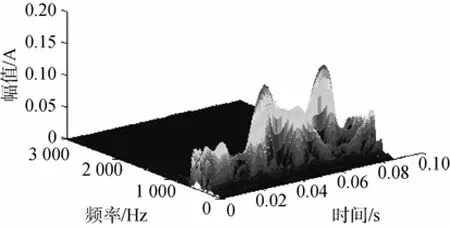
图8　基于Wigner-Ville分布的实测噪声时时频检测Fig. 8　Result of time-frequency detection of measured noise based on Wigner-Ville distribution

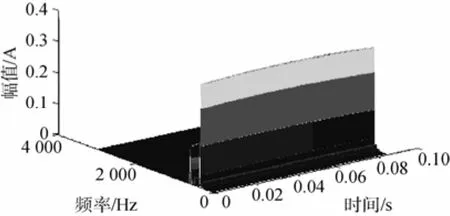
图9　基于Morlet小波变换的实测噪声时时频检测Fig. 9　Result of time-frequency detection of measured noise based on Morlet wavelet transform

为了对比研究上述3种基于时频分析的被动检测模型的检测性能，利用这3种被动检测模型对实测的10组背景噪声样本（编号1-10）和10组舰船辐射噪声样本（编号11-20）进行目标检测分析，每个样本的采样频率为Fs=6kHz，采样时间为85.3 ms。背景噪声和目标辐射噪声信号的STFT的检测统计量TSTFT，Wigner-Ville分布的检测统计量TWV和Morlet小波变换的检测统计量TWT如图10所示。

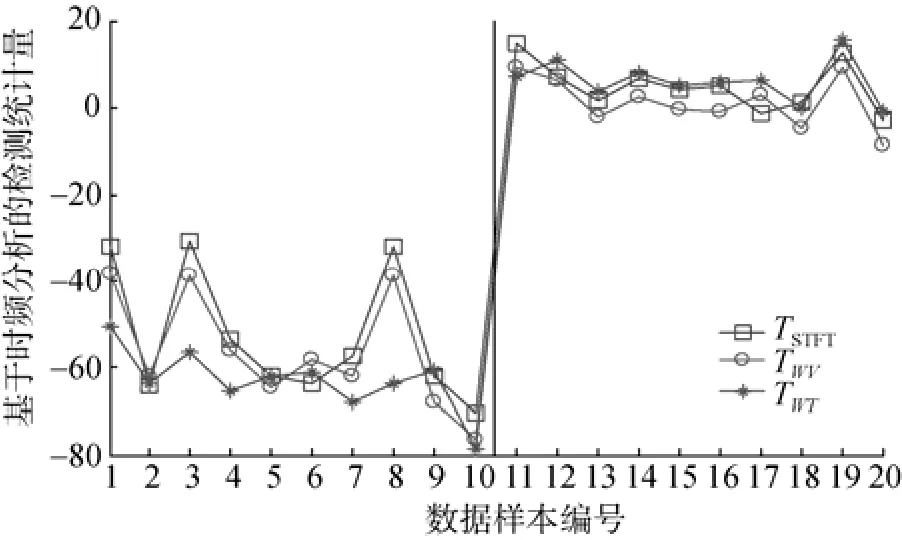
图10　背景和目标辐射噪声的时频分析检测统计量比较Fig. 10　Comparison of detection statistics of background noise and target radiated noise based on time-frequency analysis

从图10中可以看出，3种基于时频分析的被动检测模型都能将舰船目标辐射噪声样本从背景噪声样本中区分出来。对于基于STFT的检测统计量TSTFT来说, 前10个背景噪声样本的TSTFT均值为52.719 7 dB, 后10个目标辐射噪声样本的TSTFT均值为4.858 4 dB，它们之间的统计量差为57.578 1 dB。分析基于Wigner-Ville分布的检测统计量TWV可以看出，前10个背景噪声样本的TSTFT均值为-56.235 2 dB，后10个目标辐射噪声样本的TSTFT均值为1.267 8 dB，它们间的距离为57.503 0 dB。前10个背景噪声样本的Morlet小波变换的检测统计量TWT均值为-62.937 1 dB，后10个目标辐射噪声样本的TWT均值为6.091 2 dB，统计量之差为69.028 3 dB。

因此，基于STFT的被动检测模型和基于Wigner-Ville分布的被动检测模型的检测性能差不多，它们的目标辐射噪声的检测统计量比背景噪声的检测统计量大约高57.5 dB； 在基于Morlet小波变换的被动检测模型中，由于目标辐射噪声的检测统计量比背景噪声的检测统计量高出了69.0283 dB，故基于Morlet小波变换的被动检测模型的检测性能是这3种方法中最好的。从图10中可以看出，相对于另外2种方法而言，基于Morlet小波变换的检测统计量TWT对背景噪声的统计起伏是最小的，这也说明Morlet小波变换对背景噪声的抑制能力比STFT和Wigner-Ville分布都要好。

3　结束语

基于Fourier变换的传统信号处理方法很难准确获取这些水中目标的瞬态或非平稳的辐射噪声的特征，为了获取复杂环境中瞬态或非平稳水声信号的特征和高检测概率，提出了一种基于时频分析的水声目标被动检测方法，并构建了基于STFT，Wigner-Ville分布和小波变换这3种时频分析方法的被动检测模型。将提出的被动检测模型应用到实测的舰船辐射噪声数据的目标检测中，研究结果表明，尽管这3种时频分析方法都能有效地将目标检测出来，但是基于小波变换的被动检测模型的检测性能最好，其频率分辨率更高。

［1］Albert B，Francis J N. A First Course in Wavelets with Fourier Analysis［M］. 2th ed. American： John Wiley & Sons Inc，2001.

［2］张贤达，保铮. 非平稳信号分析与处理［M］. 北京： 国防工业出版社，1998.

［3］Mallat S G. 信号处理的小波导引［M］. 杨力华，戴道清，黄文良，等译. 北京： 机械工业出版社，2002.

［4］Steven M K. 统计信号处理基础-估计与检测理论［M］.罗鹏飞，译. 北京： 电子工业出版社，2006.

［5］冯讯，王守勇，万洋，等. 非高斯相关杂波背景下雷达目标统计监测方法［J］. 电波科学学报，2012，27（5）：1005-1011.

Feng Xun，Wang Shou-yong，Wan Yang，et al. Radar Target Statistical Test in Correlated Non-Gaussian Clutter Backgrounds［J］. Chinese Journal of Radio Science，2012，27（5）： 1005-1011.

（责任编辑： 杨力军）

Passive Detection Models of Underwater Acoustic Target Based on Time-Frequency Analysis

YAN Kan，LEI Jiang-Tao
（Xi′an Representative Bureau，Naval Armament Department，Xi′an 710054，China）

To extract the non-stationary or transient features of targets in complicated underwater environment and achieve high detection probability，a novel passive detection method of underwater acoustic target based on time-frequency analysis and statistical model is proposed，and three passive detection models are established based on short time Fourier transform（STFT），Wigner-Ville distribution，and wavelet transform，respectively. Target detection is conducted with these three models on the basis of the measured data of ship-radiated noise，and the results show that all three models achieve satisfactory target detection，of which the model based on wavelet transform behaves best.

time-frequency analysis； acoustic signal； target detection

TJ630.34； TN911.23

A

1673-1948（2015）01-0026-04

2014-08-25；

2014-12-12.

严侃（1980-），工程师，主要从事装备质量监督工作.