鱼雷用共形声基阵布阵方法

于一鸣，郝保安，冀邦杰，李　涛

（1. 中国船舶重工集团公司 第705研究所，陕西 西安，710075； 2. 中国船舶重工集团公司 东仪科工集团有限公司，陕西 西安，710065）

鱼雷用共形声基阵布阵方法

于一鸣1，郝保安1，冀邦杰2，李涛2

（1. 中国船舶重工集团公司 第705研究所，陕西 西安，710075； 2. 中国船舶重工集团公司 东仪科工集团有限公司，陕西 西安，710065）

为了研究不同布阵方案的共形阵所呈现出的性能差异，利用共形阵的基本布阵规则，建立了3种不同阵形的共形阵。使用常规波束形成方法，利用带障板的水听器阵元指向性计算公式和任意离散阵的指向性函数计算公式，对建立的共形阵做了指向性函数计算。通过对其水平指向性和垂直指向性的对比分析，表明了十字交叉环带型共形阵在主轴方向上具有优良的水平和垂直指向性，更适用于鱼雷武器。

鱼雷； 共形阵； 布阵规则； 水平指向性； 垂直指向性

0　引言

声学基阵是决定鱼雷自导系统性能的重要部件［1］。传统鱼雷一般采用端顶平面布阵。端顶平面阵的布阵形式单一，搜索视角较小。共形声基阵是改单纯的端顶平面布阵为沿鱼雷头部的外形曲面布阵，其结果是基阵孔径增大，总的阵元数增多，空间增益有所提高，搜索视角有所增大。

共形阵是一种与基体的外形有着共同形状的基阵。共形阵的阵元在鱼雷头部表面可能有多种布阵样式。一种布阵样式会呈现出一种独特的阵形结构形态，因此存在多种阵型的共形阵。

为了研究不同布阵方案的共形阵所呈现出来的性能差异，文中利用共形阵的基本布阵规则，并参考意大利A184鱼雷和德国DM2A4鱼雷的共形声基阵，建立了3种不同阵型的共形阵，并且通过共形阵的指向性计算对这3种布阵方案进行了研究。利用带障板的水听器阵元指向性计算公式和任意离散阵的指向性函数计算公式，对建立的共形阵做指向性函数计算，求出了各自的-3 dB波束宽度和旁瓣级，对它们的性能进行了对比分析。

1　共形阵布阵方案

依照共形阵的定义，只要阵元在基体的外表面随意分布都应看作共形阵。但是任意构造的共形阵并不适合工程化，也不利于计算。共形阵的布阵既须符合常规的布阵原则，也要遵循共形阵特有的一些要求。这些原则是： 满足空间采样定理； 阵元有规则布放； 尽可能取得足够大的孔径；阵形须拟合基体的外形； 有利于工程化［2］。

意大利A184鱼雷的声学基阵采用的是十字交叉组成的空间共形阵，共有160个阵元。水平方向有四排阵元环带，共有112个阵元； 垂直方向有四排阵元环带，共48个阵元。德国DM2A4鱼雷的声学基阵，采用的是在水平方向上4排阵元环带共形阵［3］。

共形阵在水平方向上布置的阵元数目及形状会对基阵的水平扇面产生影响； 在垂直方向布置的阵元数目及形状会对基阵的垂直扇面产生影响。以共形阵的布阵规则为依据，参考意大利A184鱼雷的声学基阵和德国DM2A4鱼雷的声学基阵，建立以下3种共形阵。

1.1四排环带型共形阵

四排环带型共形阵是将阵元在共形阵表面布成四排曲线阵。外侧曲面为半球形，球半径为0.22 m，四排曲线阵在球面上排列，每排曲线有18个阵元，相邻两阵元与球心连线的夹角为10°。阵元间距为37.5 mm，当水中声速为1 500 m/s，频率为20 kHz时，λ/2为37.5 mm。阵元间距等于半波长，满足空间采样定理。建立的72元四排环带型共形阵如图1所示。

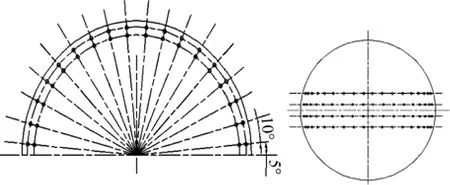
图1　四排环带型共形阵的顶视图及前视图Fig. 1　Top view and front view of four-row ring type conformal array

1.2六排环带型共形阵

六排环带型共形阵是将阵元在共形阵表面布成六排曲线阵。外侧曲面为半球形，球半径为0.22 m。六排曲线阵在球面上排列，每排曲线有18个阵元，相邻两阵元与球心连线的夹角为10°。阵元间距为37.5 mm，当水中声速为1 500 m/s，频率为20 kHz时，λ/2为37.5 mm。阵元间距等于半波长，满足空间采样定理。建立的108元六排环带型共形阵如图2所示。

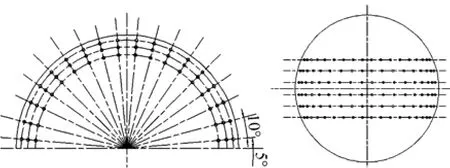
图2　六排环带型共形阵的顶视图及前视图Fig. 2　Top view and front view of six-row ring type conformal array

1.3十字交叉环带型共形阵

十字交叉环带型共形阵是将阵元在共形阵表面布成十字交叉型。外侧曲面为半球形，球半径为0.22 m，四排曲线阵在球面上排列，每排曲线有18个阵元，在垂直方向上增加四排阵元，每排4个阵元。相邻两阵元与球心连线的夹角为10°。阵元间距为37.5 mm，当水中声速为1 500 m/s，频率为20 kHz时，λ/2为37.5 mm。阵元间距等于半波长，满足空间采样定理。建立的88元十字交叉环带型共形阵如图3所示。

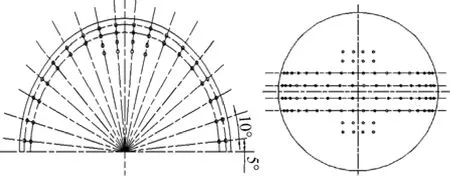
图3　十字交叉环带型共形阵的顶视图及前视图Fig. 3　Top view and front view of cross ring type conformal array

2　任意形状离散阵的指向性计算

对于多阵元密集布放的球面阵，其数学模型的建立基于以下假设： 共形阵阵元完全相同，都可看作声学中心处的点阵元，阵元相互间无影响。

一个无方向性的水听器放在声障板面上后，受声障板影响变得有一定的指向性［4］。在一定频率下测得的指向性平均值可以近似为

式中，-90°≤θ≤90°，θ为阵元声主轴与信号入射方向的夹角。指向性如图4所示。

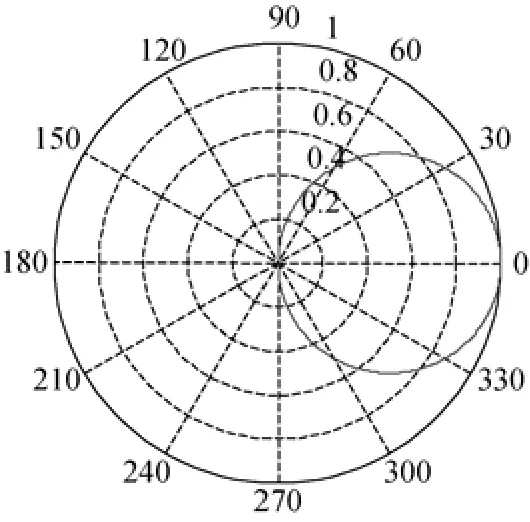
图4　带障板的水听器指向性Fig. 4　Directivity of array element with baffle

认为共形阵的阵元都具有上式的指向性。同时把共形阵看作具有一定形状的空间阵列，这就建立了共形阵的简化模型。

对于一个任意分布的离散阵，各个阵元的位置可用矢量ri（xi，yi，zi）来表示，如图5所示。

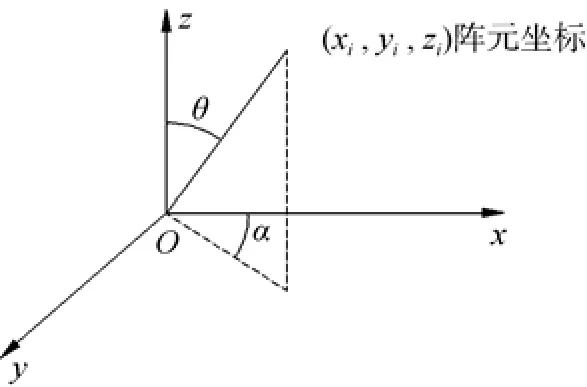
图5　基阵坐标系Fig. 5　Coordinate system of an array

对于任意方向发射声线的单位矢量e（α,）θ可表示为

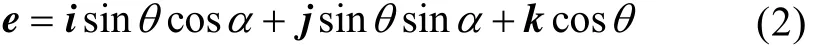
式中： θ为声线与z轴的夹角； α为声线在xoy平面上的投影与x轴的夹角。若利用相控技术使主波束控制在（α0，θ0）上，令其单位矢量

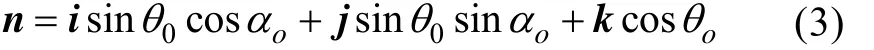
以坐标原点为参考点，则第i号阵元向任意方向发射的声线相对于参考点的声程差

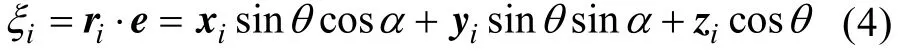
第i号阵元向主波束方向发射的声线相对于参考点的声程差

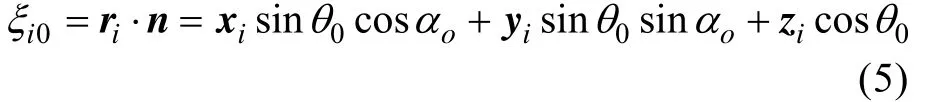
因此，第i号阵元向任意方向发射的声线相对于向主波束方向发射的声线相位差为

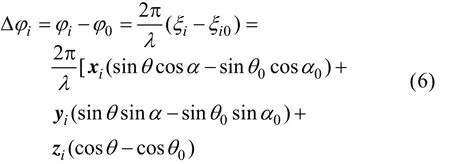
在（α，）θ方向上场点的声压是所有阵元辐射声波在场点处声压值的线性叠加，若阵元具有相同的发射响应，对于任意形状离散基阵的3D归一化指向性函数可表示为

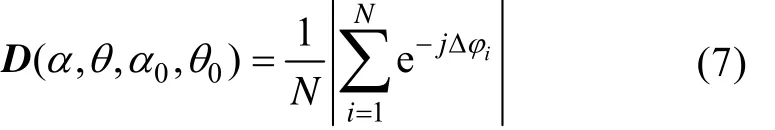
利用乘积定理，由式（1）和式（7）可求得共形阵的指向性函数

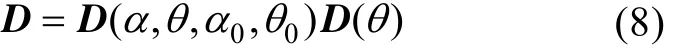
3　共形阵指向性分析

为了研究上述3种共形阵的搜索扇面，沿其水平方向和垂直方向进行常规波束形成。设水中声速为1 500 m/s，频率为20 kHz。为便于对比，选取0°，30°，60°共3个方向进行分析。

3.1四排环带型共形阵的指向性分析

在基阵工作时的水平方向，当波束主瓣指向0°，30°和60°时形成的3个波束的水平指向性如图6所示，垂直指向性如图7所示。

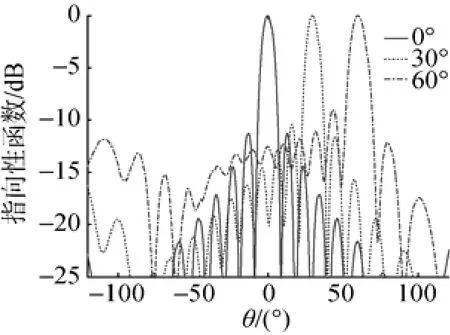
图6　四排环带型共形阵的水平波束图Fig. 6　Horizontal beam pattern of four-row ring type conformal array

分析图6中基阵的水平波束，用以研究基阵的水平搜索扇面。当水平波束主瓣指向0°时，束宽为7.9°； 指向30°时，束宽为8.5°； 指向60°时，束宽为10.8°。波束宽度逐渐增大，但变化不大。

图7　四排环带型共形阵的垂直波束图Fig. 7　Vertical beam pattern of four-row ring type conformal array

分析图7中基阵的垂直波束，当水平波束主瓣指向0°时，束宽为25.2°； 指向30°时，束宽为25.1°；指向60°时，束宽为25.2°。波束宽度基本不变。

3.2六排环带型共形阵的指向性分析

在基阵工作时的水平方向，当波束主瓣指向0°，30°和60°时形成的3个波束的水平指向性如图8所示，垂直指向性如图9所示。

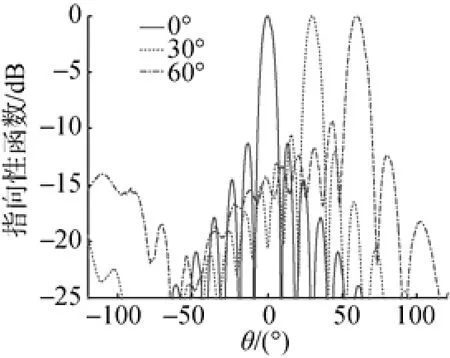
图8　六排环带型共形阵的水平波束图Fig. 8　Horizontal beam pattern of six-row ring type conformal array

分析图8中基阵的水平波束，用以研究基阵的水平搜索扇面。当水平波束主瓣指向0°时，束宽为7.8°； 指向30°时，束宽为8.5°； 指向60°时，束宽为10.8°。波束宽度逐渐增大，但变化不大。

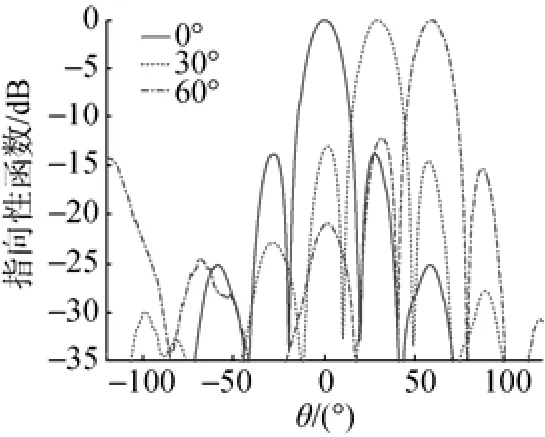
图9　六排环带型共形阵的垂直波束图Fig. 9　Vertical beam pattern of six-row ring type conformal array

分析图9中基阵的垂直波束，当水平波束主瓣指向0°方向时，束宽为17.0°； 指向30°方向时，束宽为17.1°； 指向60°方向时，束宽为17.0°。波束宽度基本不变。

3.3十字交叉环带型共形阵的指向分析

在基阵工作时的水平方向，当波束主瓣指向0°，30°和60°时形成的3个波束的水平指向性如图10所示，垂直指向性如图11所示。

图10　十字交叉环带型共形阵的水平波束图Fig. 10　Horizontal beam pattern of cross ring type conformal array

分析图10中基阵的水平波束，用以研究基阵的水平搜索扇面。当水平波束主瓣指向0°时，束宽为7.9°； 指向30°时，束宽为8.5°； 指向60°时，束宽为10.8°。波束宽度逐渐增大，但变化不大。

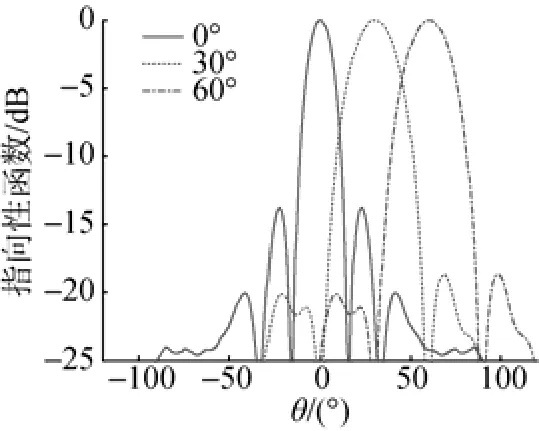
图11　十字交叉环带型共形阵的垂直波束图Fig. 11　Vertical beam pattern of cross ring type conformal array

分析图11中基阵的垂直波束，当水平波束主瓣指向0°时，束宽为13.6°； 指向30°时，束宽为25.5°； 指向60°时，束宽为25.2°。波束宽度在主瓣指向0°时较窄。

3.4指向性图对比分析

为了研究以上3种阵型的共形阵搜索扇面水平波束和垂直垂直波束的差异，对以上3种共形阵的指向性进行横向对比分析。

当3种共形阵波束主瓣都指向0°时水平波束图对比见图12。表1列出了0°时水平波束图的波束宽度和旁瓣级。分析图12和表1数据可知，3种共形阵在水平指向性上波束宽度基本相同。

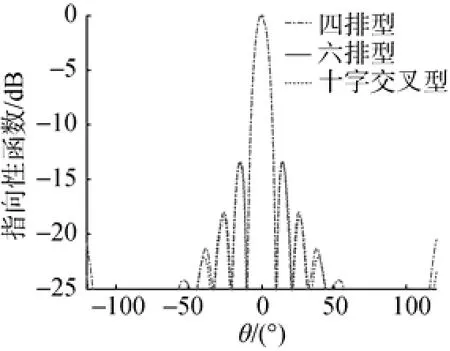
图12　0°时水平波束图对比Fig. 12　Comparison of horizontal beam patterns at 0°

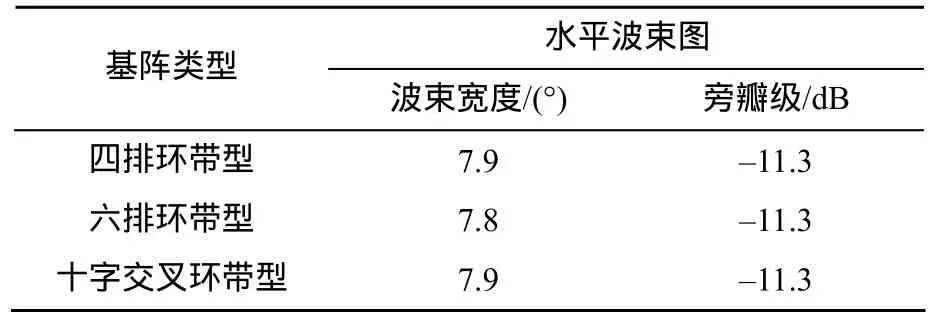
表1　0°时水平波束图的波束宽度和旁瓣级Table 1　Beam width and sidelobe of horizontal beam pattern at 0°

图13是当3种共形阵波束主瓣指向60°时的水平指向图对比。表2列出了60°时水平波束图的波束宽度和旁瓣级。分析图13和表2数据可知，当波束主瓣指向60°时，3种共形阵的波束宽度基本相当。与波束主瓣指向0°时相比，波束宽度有所增大。

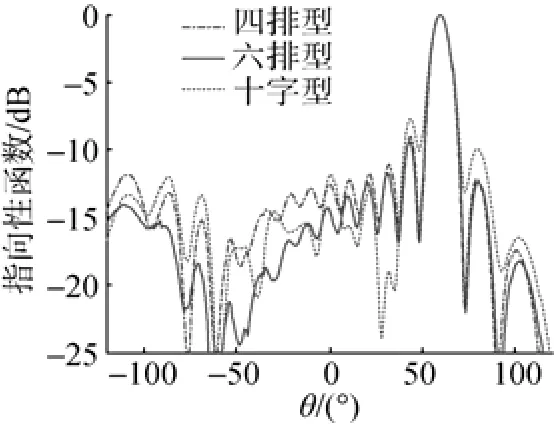
图13　60°时水平波束图对比Fig. 13　Comparison of horizontal beam patterns at 60°

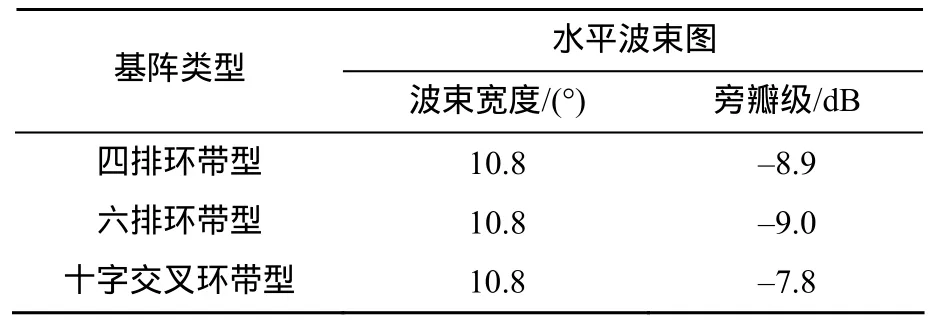
表2　60°时水平波束图的波束宽度和旁瓣级Table 2　Beam width and sidelobe of horizontal beam pattern at 60°

当3种共形阵波束主瓣都指向0°时的垂直指向见图14。表3 给出了0°时垂直波束图的波束宽度和旁瓣级。分析图14和表3数据可知，六排环带型共形阵与四排环带型共形阵在垂直指向性上相比波束宽度减小； 十字交叉型共形阵与六排环带型共形阵相比，具有更小的波束宽度。

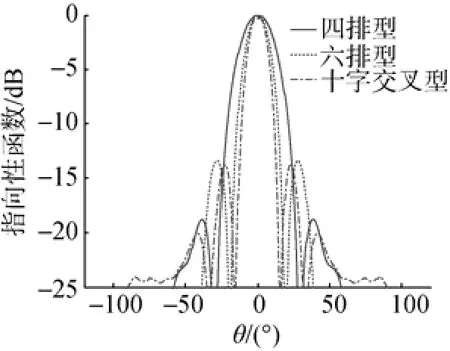
图14　0°时垂直波束图对比Fig. 14　Comparison of vertical beam patterns at 0°

表3　0°时垂直波束图的波束宽度和旁瓣级Table 3　Beam width and sidelobe of vertical beam pattern at 0°

当3种共形阵的波束主瓣都指向60°时的垂直指向图对比如图15所示。表4 给出了60°时垂直波束图的波束宽度和旁瓣级。分析图15和表4数据可以发现，当波束主瓣指向60°时，四排环带型共形阵与十字交叉环带型共形阵在垂直指向性上相比，波束宽度相当； 六排环带型共形阵具有更小的波束宽度。

通过以上分析可以发现3种共形阵具有如表5所示的特征。

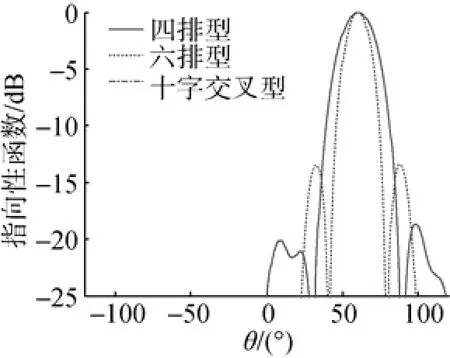
图15　60°时垂直波束图对比Fig. 15　Comparison of vertical beam patterns at 60°

表4　60°时垂直波束图的波束宽度和旁瓣级Table 4　Beam width and sidelobe of vertical beam pattern at 60°

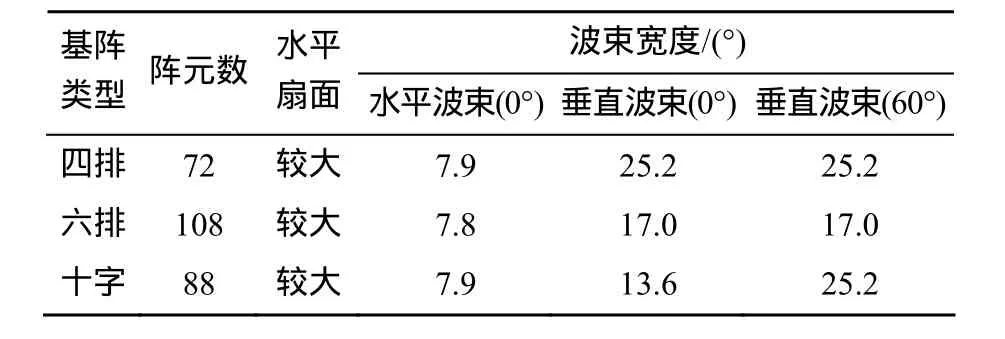
表5　共形阵波束对比分析Table 5　Comparison of conformal array beams

1）六排环带型共形阵与四排环带型共形阵相比较，水平扇面相当。在水平方向上，二者的波束宽度差异很小； 在垂直方向上，六排环带型共形阵的波束宽度较小。

2）十字交叉环带型共形阵与六排、四排环带型共形阵相比水平扇面相当。在水平方向上，波束宽度和前两者差异很小； 在垂直方向上，当波束主瓣指向0°时，十字交叉环带型共形阵的波束宽度最小。

3）3种共形阵与传统平面阵相比，在相同的基阵空间下，平面阵一般只能布放52个阵元［5］。由此可见，相同的空间下，共形阵可布放的阵元数大于平面阵。

4）3种共形阵与A184鱼雷和DM2A4鱼雷的声学基阵相比，其中A184鱼雷的阵元数目达到了160个，阵元数目过多会导致对阵元信号采集的通道数量要求更多，使自导系统的结构更为复杂［6］。比较而言，十字交叉环带型共形阵的阵元数虽只有88个，但已获得了较好的水平和垂直指向性。

4　结论

文中利用共形阵的基本布阵规则，参考意大利A184鱼雷和德国DM2A4鱼雷的共形声基阵，建立了3种不同阵型的共形阵。利用带障板的水听器阵元指向性计算公式和任意离散阵的指向性函数计算公式，对建立的共形阵做了指向性函数计算，进行了常规波束形成。求出了各自的-3 dB波束宽度和旁瓣级，对它们的指向性进行了对比分析。通过对指向性图、波束宽度和旁瓣级的计算和对比分析，可以得出如下结论。

1）3种阵形的水平波束宽度相当，水平扇面都较大。

2）四排环带型共形阵阵元数目较少，垂直波束较宽，适用于对垂直波束要求不高的场合。

3）六排环带型共形阵阵元数目较多，垂直波束较窄，适用于对垂直波束有一定要求的场合。

4）十字交叉环带型共形阵的阵元数目介于两者之间，在0°方向上垂直波束最窄，适用于在主轴方向上对垂直波束要求较高的场合，适用于鱼雷武器。

［1］石秀华，王晓娟. 水中兵器概论（鱼雷分册）［M］. 西安：西北工业大学出版社，2005.

［2］李贵斌. 声纳基阵设计原理［M］. 青岛： 海洋出版社，1985.

［3］夏永伟. 水下自导共形阵的接收特性研究［D］. 西安：西北工业大学，2007.

［4］张俊. 鱼雷共形阵发射声场计算及波束优化研究［D］.西安： 中国船舶重工集团公司第705研究所，2007.

［5］杨博，孙超，陈亚林. 基于声场预报的共形阵波束优化方法与实验研究［J］. 鱼雷技术，2006，14（1）： 19-20.

Yang Bo，Sun Chao，Chen ya-lin. Conformal Array Beampattern Optimization Method and Experimental Research Based on Sound Field Forecast［J］. Torpedo Technology，2006，14（1）： 19-20.

［6］崔绪生. 国外鱼雷技术进展综述［J］. 鱼雷技术，2006，14（3）： 6-11.

Cui Xu-Sheng. A Summary of Progress in Torpedo Technology Over the World［J］. Torpedo Technology，2006，14（3）： 6-11.

（责任编辑： 杨力军）

A Conformal Array Arrangement Method for Torpedo

YU Yi-ming1，HAO Bao-an1，JI Bang-jie2，LI Tao2
（1. The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China； 2. The DongYi Science Technology & Industry Group Co. Ltd. Limited，China Shipbuilding Industry Corporation，Xi′an 710065，China）

To explore the performances of different arrangements of conformal array，three different arrangements of conformal array are established based on the basic rules of arrangement. By using the conventional beamforming method，the directivity formulae of the array element with baffle and any discrete array，the directivity function of the established conformal arrays are calculated. The horizontal and vertical directivities are analyzed and compared. The results show that the cross ring type conformal array is more suitable for torpedo weapon due to its better horizontal and vertical directivities in the main axis.

torpedo； conformal array； arrangement rule； horizontal directivity； vertical directivity

TJ630.34； TB56

A

1673-1948（2015）01-0014-06

2014-10-25；

2014-12-12.

于一鸣（1987-），男，在读硕士，主要从事声自导与信号处理技术研究.