潜艇水下武器发射后海水喷流噪声数值仿真

练永庆,　郭　煜,　张孝芳

(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军潜艇学院 战略导弹与水中兵器系, 山东 青岛, 266071)

潜艇水下武器发射后海水喷流噪声数值仿真

练永庆1,郭煜1,张孝芳2

(1. 海军工程大学 兵器工程系, 湖北 武汉, 430033; 2. 海军潜艇学院 战略导弹与水中兵器系, 山东 青岛, 266071)

为了研究武器发射出管后的海水喷流噪声, 将发射管比拟为水下圆管, 通过发射装置水下发射过程的3D流场仿真, 获取了武器出管后发射管口海水喷流的流场特性, 在此基础上采用基于Lighthill声学类比的积分方法对水下圆管自由喷流噪声进行了计算与分析。结果表明, 喷流噪声的能量主要集中在100 Hz以下的低频范围内, 水下武器发射后的海水喷流噪声源并不是总发射噪声的主要组成。

潜艇水下发射; 海水喷流; 噪声; 仿真

0　引言

潜艇往复活塞水压平衡式发射装置[1]水下发射武器产生的发射噪声主要有发射时水压力脉冲激励产生流致结构噪声、发射动力装置机械结构振动冲击产生的噪声、发射后气缸废气艇内排气产生噪声等。此外, 武器在出管后, 发射管内的海水由于惯性作用会继续向前运动, 在发射管前部形成水喷流, 因此该喷流有可能是一个重要的发射噪声源。为了对该水下喷流噪声进行研究,文中将发射管的水下喷流简化为水下圆管的自由喷流, 通过进行发射过程3D流场仿真获取发射后喷流流场, 再根据Lighthill声学比拟理论对该水下圆管自由湍喷流的噪声辐射问题进行计算与分析。

1　水下发射过程3D流程仿真

往复活塞水压平衡式发射装置主要由两大子系统构成[1]: 气动系统和水压平衡系统, 并且2个子系统的工作介质完全不同, 前者为压缩空气, 后者为海水。两者通过活塞组件的运动实现了发射能量由发射气瓶向武器的传递。在整个过程中压缩空气与海水以及运动部件之间始终存在强烈的相互耦合作用。文中采用气动系统1D模型和水压平衡系统3D模型联合仿真的方案进行发射过程的数值仿真。这种方法是把从Fluent解算器得到水缸活塞和武器所受的流体作用力代入气瓶、气缸、活塞和武器的1D动力学方程组, 采用数值积分求得活塞和武器的运动速度反过来作为Fluent解算器中活塞和武器动边界的运动参数。下面对动力学方程组及3D流场仿真介绍如下。

1) 1D动力学方程组

仿真中所用的1D动力学方程组主要包括的相关数学模型如下。

a. 气瓶数学模型

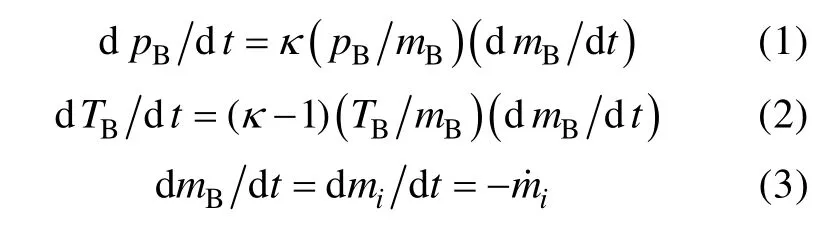
式中: pB为发射气瓶瞬时压力; mB为发射气瓶内气体的瞬时质量; κ为空气绝热指数; TB为发射气瓶内气体的瞬时温度;dmid t为通过发射阀流入发射管的气体质量流量。

b. 发射阀数学模型

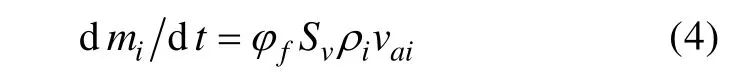
式中:fφ为发射阀的空气流量系数; Sv为发射阀开启的流通面积;iρ为发射阀特形孔处气流的密度; vai为气流通过发射阀的流速。

c. 气缸数学模型

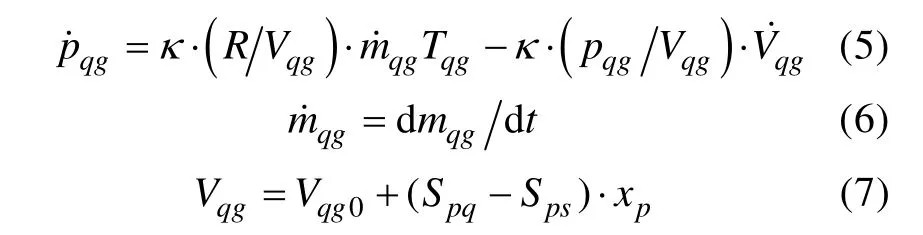
式中: Vqg,mqg,pqg,Tqg分别为气缸控制体内空气体积、质量、压力、温度; Vqg0为气缸控制体初始体积; m.qg为气缸内空气质量变化率; xp为气缸活塞位移; Spq为气缸活塞横截面积; Sps为活塞杆横截面积。

d. 活塞组件运动模型

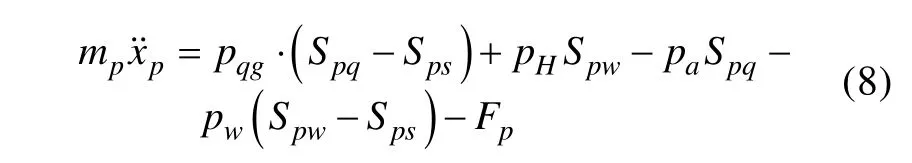
式中: mp为活塞组件质量(包括气缸活塞、水缸活塞及活塞杆);pH为水缸前端海水外部环境压力;Spw为水缸活塞横截面积;pa为潜艇舱室压力;pw为水缸压力;Fp为活塞组件与气缸壁、水缸壁的摩擦力。

e. 鱼雷发射管内运动模型

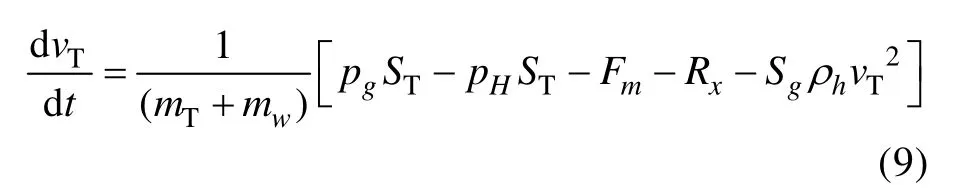
式中: vT为鱼雷管内运动速度; pg为发射管内海水压力; ST为鱼雷圆柱段横截面积; mT为鱼雷质量; mW为随鱼雷一起运动的海水质量; Fm为鱼雷与发射管之间的机械摩擦阻力; Rx为鱼雷流体运动阻力; Sg为发射管横截面积。

2) 3D流场仿真

发射装置内部瞬态流场的计算采用压力的隐式算子分割算法(pressure implicit with splitting of operators, PISO)[2]。在发射装置内部瞬态流场的数值仿真中, 包含水缸活塞和鱼雷2个运动物体, 它们的运动造成了流场计算区域边界的移动。为此在瞬态流动计算中, 综合采用滑移网格和动网格技术, 考虑不同时刻运动域和静止域间的相对位置以及移动边界对计算域网格的影响,以准确模拟流体流动与物体运动相互耦合的瞬态流动。

整个发射装置3D流场的计算区域模型如图1所示。

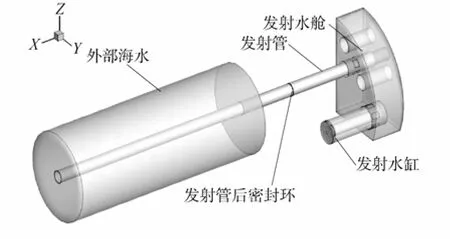
图1　3D流场计算区域示意图Fig. 1　Schematic of computational domain of threedimensional flow field

3) 仿真结果

通过仿真可获得整个发射过程不同时刻的流场仿真, 这里给出部分流场仿真结果如图2~图5所示。此外, 还获得武器出管后海水喷流流场仿真结果, 其中部分仿真结果如图6~图9所示。

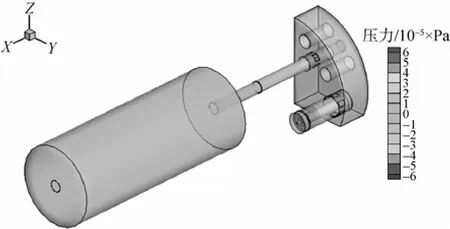
图2　发射时刻t=0.3 s时流体域内的海水压力云图Fig. 2　Pressure contour of seawater in the flow field when t=0.3 s

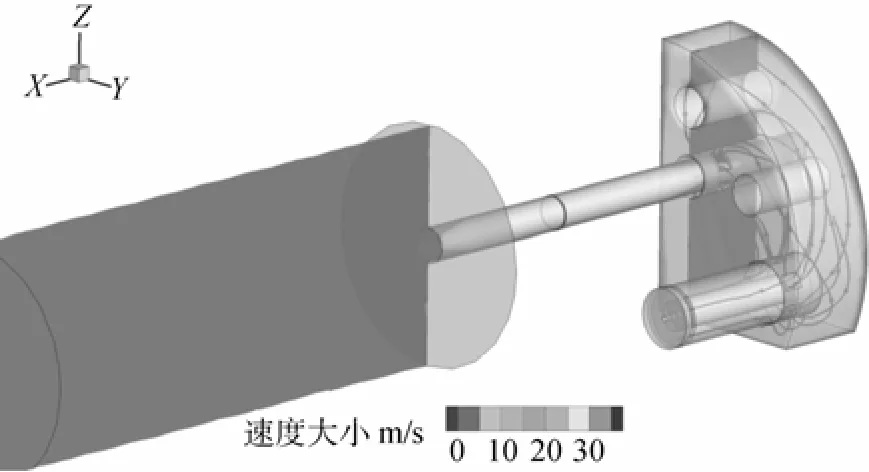
图3　发射时刻t=0.3 s时流体域内的海水流线和速度云图Fig. 3　Velocity contour and flow line of seawater in the flow field when t=0.3 s

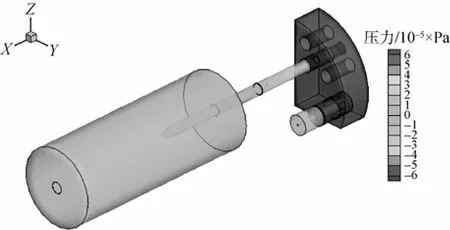
图4　发射时刻t=0.6 s时流体域内的海水压力云图Fig. 4　Pressure contour of seawater in the flow field when t=0.6 s

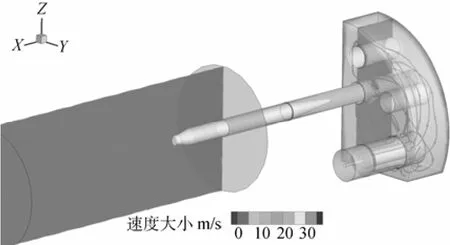
图5　发射时刻t=0.6 s时流体域内的海水流线和速度云图Fig. 5　Velocity contour and flow line of seawater in the flow field when t=0.6 s

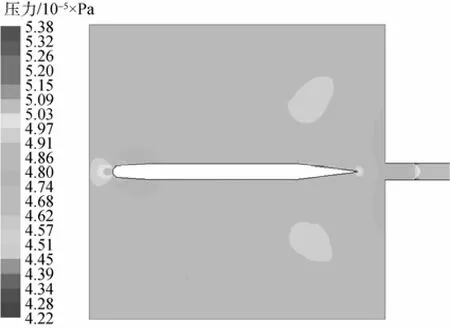
图6　t=1.1 s时刻发射管口附近压力云图Fig. 6　Pressure contour of seawater near the nozzle when t=1.1 s

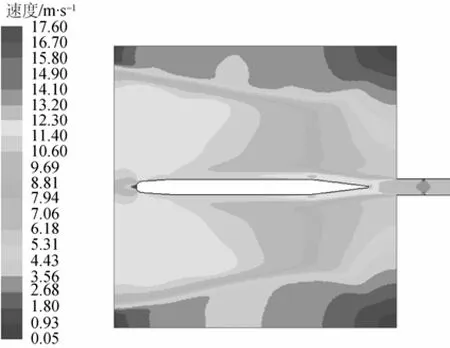
图7　t=1.1 s时刻发射管口附近速度云图Fig. 7　Velocity contour of seawater near the nozzle when t=1.1 s

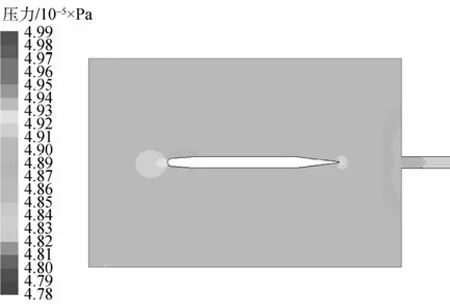
图8　t=1.6 s时刻发射管口附近压力云图Fig. 8　Pressure contour of seawater near the nozzle when t=1.6 s

2　水下圆管自由喷流噪声仿真与建模

在喷流噪声的理论研究方面, 气动声学的发展要早于水声学, 国内外很多关于水射流湍流噪声的研究都是在气动声学基础上展开的[3-4], 并将气动声学的理论推广到包括水声学的流体声学,也通过试验验证了理论的正确性[5], 为此采用基于Lighthill声学类比的积分方法对水下圆管自由喷流噪声进行计算机分析。

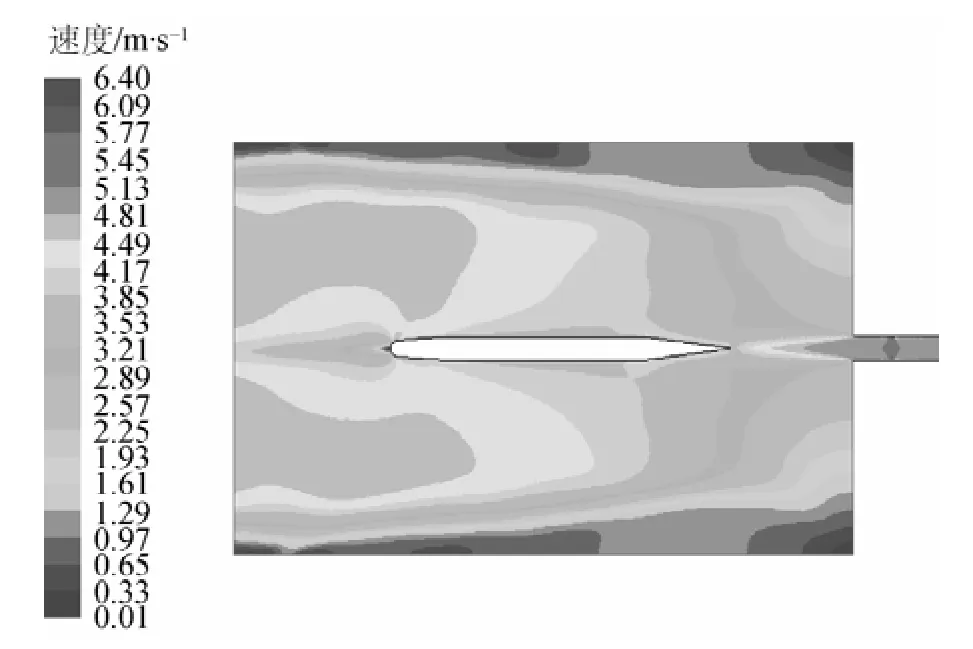
图9　t=1.4 s时刻发射管口附近的速度云图Fig. 9　Velocity contour of seawater near the nozzle when t=1.4 s

声学类比本质上是对声的产生和传播进行解耦, 从而把声学分析与流场求解过程相分离。通过求解发射过程的非定常NS方程, DES或LES等得到发射管口近场流场, 然后借助于波动方程的解析式积分解便能够进行声场的预报。

仿真中喷流噪声的声学计算主要基于Ffowcs Williams and Hawkings(FW-H)方程[6]及其积分解。FW-H方程实际上是通过对连续性方程和NS方程进行处理而得到的非齐次波动方程

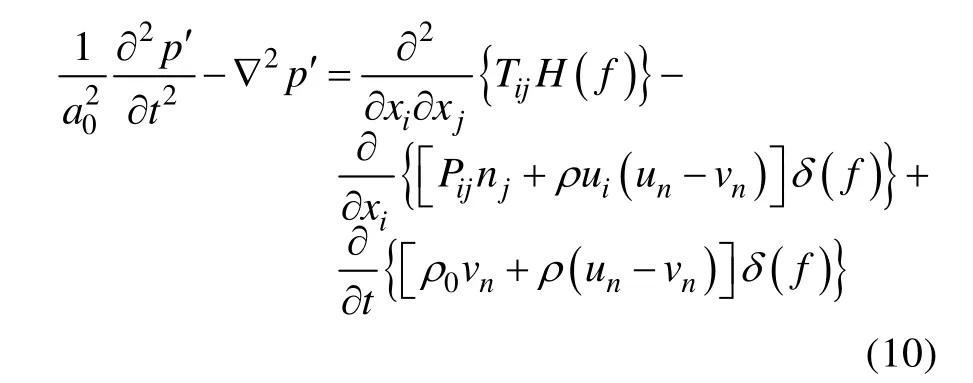
其中: ui为xi方向的流体速度分量; un为面f=0法向流体速度分量; vi为xi方向面速度分量; vn为曲面法向面速度分量; δ（f）为Dirac函数; H（f）为Heaviside 函数。p′为远场声压, p′=p-p0；f=0是为了使外部流动问题(f＞0)“嵌入”无边界空间而引入的数学曲面,从而可以方便地应用广义函数理论和自由空间格林函数来求解。曲面f=0对应于源面(发射面),它可以和固体边界面一致(不可穿透), 也可以脱离边界面(可穿透)。ni是指向曲面外(f＞0)的单位法向量; a0是远场声速; Tij为Lighthill应力张量, 有

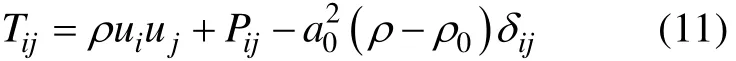
其中, Pij为压缩应力张量, 对于斯托克斯流体, 有

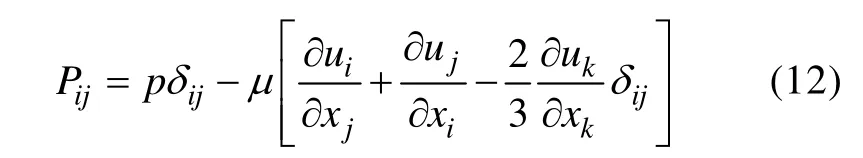
应用自由空间格林函数可得到方程(10)的解,其完整解包括面积分和体积分两部分。面积分代表单极子、偶极子声源的作用及源面所包围的四极子声源的作用, 而体积分则代表源面外区域四极子声源的作用。

FW-H方程采用了Lighthill声学类比的最基本形式, 能够预报等效于单极子、偶极子及四极子的声源。在FLUENT仿真中应用时采用时域积分公式, 通过求解一些面积分而直接计算指定接收器位置的声压或声学信号的时间序列。

3　计算结果与分析

根据发射过程3D流场仿真获得的海水喷流仿真结果, 利用方程(10)中的模型与方法计算了水下圆管自由湍喷流四极子辐射噪声的声压频谱。以下给出武器出管后海水喷流的仿真结果,其中声压的测点坐标是相对于发射管口(喷口)中心点的坐标值, 仿真中给出某时刻(50 m, 50 m)以及(5 000 m, 5 000 m)两处的声压仿真结果。

对仿真结果进行分析可知:

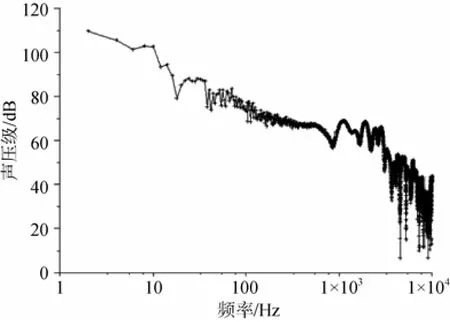
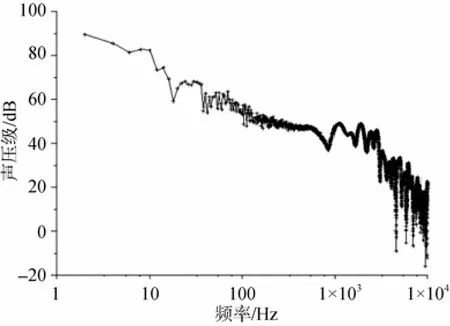
1) 武器出管后喷流噪声的声能量主要集中于100 Hz以内, 频率大于100 Hz的噪声级在(50 m, 50 m)处均小于80 dB, 在(5 000 m, 5 000 m)处均小于50 dB(见图10和图11);

2) 喷流噪声随着与喷口间距离的增大而逐渐衰竭, 在距离50 m处的最大噪声级为115 dB(见图8), 第2种仿真条件下距离5 000 m处远场最大噪声级为85 dB(见图11)。

3) 潜艇水下武器发射后, 在(50 m, 50 m)附近、100 Hz以内的喷流噪声级略大于同频率的海洋环境噪声(频率为100 Hz的海洋环境噪声级为90 dB左右)[7], 而(5 000 m, 5 000 m)处的喷流噪声基本小于海洋环境噪声。由此可见, 潜艇水下武器发射后的海水喷流噪声源对总发射噪声的贡献是较低的。

4　结束语

针对潜艇水下武器发射过程中武器出管后的喷流噪声问题, 将潜艇武器发射管比拟为水下圆管, 在通过进行发射过程3D流场仿真获取了武器出管后的海水喷流的基础上, 运用Lighthill声学比拟理论研究了水下圆管自由喷流的噪声辐射问题。从仿真结果来看, 喷流噪声的能量主要集中在100 Hz以下的低频范围内, 其噪声级在潜艇近场(50 m以内)略大于海洋环境噪声, 而在远场(5 000 m以外)则基本小于环境噪声。由此可见,潜艇水下武器发射后的海水喷流噪声对潜艇总发射噪声的贡献不大, 潜艇发射噪声源主要集中在流致结构振动噪声、发射动力装置机械结构振动冲击产生的噪声、发射后气缸废气艇内排气产生噪声这三方面。

在仿真中为了简化问题的研究将发射管喷流视为水下圆管的自由喷流, 但在实际中, 发射管口并非为自由端, 海水喷流离开发射管口后还与管口附近潜艇壁面产生相互作用, 其噪声产生与传播机理将更为复杂, 将需要进一步的深入研究。

[1] 练永庆, 王树宗. 武器发射装置设计原理[M]. 北京:国防工业出版社, 2012: 65-66.

[2] Issa R I. Solution of Implicitly Discredited Fluid Flow Equations by Operator Splitting[J]. Journal of Computational Physics, 1986(62): 40-65.

[3] Tam C K W. Jet Noise: Since 1952[J]. Theoretical and Computational Fluid Dynamics. 1998, 10(1): 393-405.

[4] 李晓东, 旻江, 高军辉. 计算气动声学进展与展望[J].中国科学: 物理学力学天文学, 2014, 44(3): 234-248.

Li Xiao-dong, Jiang Min, Gao Jun-hui. Progress and Prospective of Computational Aeroacoustics[J]. Scientia Sinica(Physica, Mechanica& Astronomica), 2014, 44(3): 234-248.

[5] 王春旭. 水下湍射流及壁面湍流噪声预报方法[D]. 武汉: 华中科技大学, 2009: 100-102.

[6] Ffowcs W J E, Kempton A J. The Noise from the Largescale Structure of a Jet[J]. Journal of Fluid Mechanics, 1978, 84(4): 673-694.

[7] 郭新毅, 马力. 环境变化条件下海洋环境噪声统计分析[C]//2010中国西部地区声学学术交流会. 云南: 中国声学学会, 2010: 338-341.

(责任编辑: 许妍)

Simulation on Seawater Jet Noise after Submarine Underwater Launching

LIAN Yong-qing1,GUO Yu1,ZHANG Xiao-fang2
(1. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China; 2. Department of Ballistic Missile and Underwater Weapon, Naval Submarine Academy, Qingdao 266071, China)

To study the noise of the seawater jet from a submarine launch tube after a weapon leaving the tube, simulation on three-dimensional flow field of the launching process is conducted, and the fluid field of the seawater jet at nozzle after the weapon leaving the tube is obtained. The free jet noise of underwater round pipe is calculated using the Lighthill acoustic analogy integral method based on the seawater jet fluid characteristic. Calculation result shows that the energy of seawater jet noise concentrates in the low frequency noise (lower than 100 Hz), and the seawater jet noise is not the main component of the overall launching noise.

submarine underwater launching; seawater jet; noise; simulation

TJ635

A

1673-1948(2015)01-0061-05

2014-10-25;

2014-11-14.

练永庆(1973-), 男, 博士, 副研究员, 研究方向为水中兵器发射技术.