水下涡轮机系统转速闭环控制研究

罗　凯，张学雷，王晓欣，罗　鑫

（西北工业大学 航海学院，陕西 西安，710072）

水下涡轮机系统转速闭环控制研究

罗凯，张学雷，王晓欣，罗鑫

（西北工业大学 航海学院，陕西 西安，710072）

应用于高速水下航行器的开式涡轮机系统具有耗气量低、焓降大和结构简单等特点，但该系统对工况敏感。采用调节燃料泵泵角的闭环控制策略，建立开式涡轮机动力系统及其泵角执行机构的数学模型，设计合理的控制算法并研制转速闭环控制器，首次实现了水下涡轮机的无级变速控制。半物理仿真试验结果表明，所设计的控制器可保证系统转速在变工况下跟随指令转速，转速调节的过渡时间不大于7 s，最大转速偏差不大于20 r/min，燃烧室压强超调不大于5%，保证了系统的安全性，可以有效地支持航行器新型制导规律的实现。

自主式水下航行器； 开式涡轮机； 闭环控制； 控制器； 无级变速

0　引言

受制于当前材料、设计和工艺水平等因素，应用于高速水下航行器的筒形活塞发动机的性能潜力已发挥至极限，难以在目前500 kW的水平上进一步提高［1］。采用涡轮机作为动力推进系统，是进一步提高水下航行器航速的主要选择之一。水下涡轮机具有耗气量低、焓降大、结构简单等特点，然而开式涡轮机动力系统对工况的敏感程度远远超过活塞机系统［2］，为获得稳定可控的转速，研究水下涡轮机系统的闭环控制十分必要。

相比传统的开环控制策略，闭环控制系统能够提供航行器弹道控制所需的燃料余量、当前航深下的可能变速范围等计算参量，可实现航行器的最佳导引弹道。国外在该方面的研究较早并已成功应用于水下航行器。如英国的spearfish鱼雷已很好地解决了转速控制与调节的难题，该鱼雷采用开式循环燃气涡轮机动力系统，最高航速70 kn，最大航深可达900 m［3］。国内对于水下动力系统的闭环控制研究多针对活塞机系统，如西北工业大学的李代金等人在实验室条件下实现对水下活塞机的无级变速控制［5］。然而尚未发现成功实现水下涡轮机系统转速闭环控制的相关文献。

文章针对开式涡轮机动力系统，建立系统的数学模型，设计合理控制算法，研制应用于涡轮机的转速闭环控制器，并通过半物理仿真试验验证了设计的实用性。

1　水下涡轮机转速闭环控制策略

水下涡轮机动力推进系统原理如图1所示，其主要由电控变排量燃料泵、涡轮发动机、燃烧室、挤代式燃料储仓、推进器、转速闭环控制器、辅机（中频电机、滑油泵、海水泵等辅件）等组成［4］。

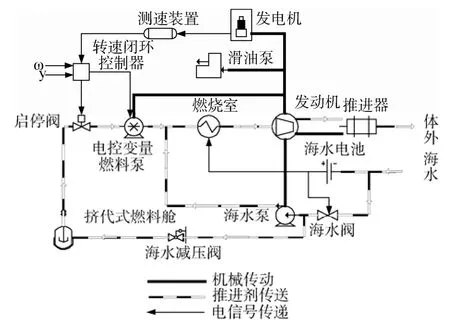
图1　水下涡轮机动力推进系统原理图Fig. 1　Principle of underwater turbine propulsion system

海水进入海水电池后，通过电爆管引燃燃烧室里的固体药柱，系统随之启动。涡轮机输出轴带动推进器和辅机转动，海水经海水泵增压后，一部分用于燃烧室冷却，另一部分通过减压阀进入燃料储仓挤代燃料，确保燃料泵泵前压力恒定。燃料经燃料泵增压通过单向阀进入燃烧室，经喷嘴雾化后燃烧，产生高温高压燃气推动涡轮机做功。涡轮机输出转速经过减速器适当降低后驱动螺旋桨旋转，同时，做功后的低温低压废气经推进轴内孔排出体外。

转速闭环控制器接收的指令为上位机发送的启动指令、转速指令和航深指令等信号，所接受的反馈信号是涡轮机的当前转速，因涡轮机以恒速比带动发电机，所以只要用转速传感器测出发电机转速即可计算出涡轮机转速。燃料泵斜盘角（对应泵的排量）受控于转速闭环控制器。控制器根据当前指令及反馈转速，输出控制信号到变量燃料泵伺服系统中，伺服系统的执行机构——伺服电机根据信号适当调整燃料泵泵角，改变进入燃烧室的燃料流量，以实现对航行器转速控制。

2　系统模型

2.1动力系统模型

对于使用泵供式、涡轮发动机的开式循环热动力推进系统，其系统机理模型由以下方程构成。航行器纵平面运动学方程

纵平面动力学方程，

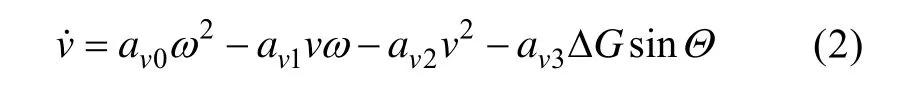
燃料泵执行机构特性

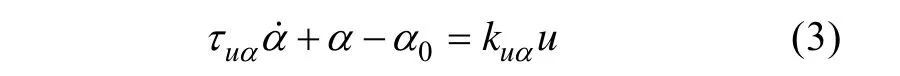
燃烧室压强特性

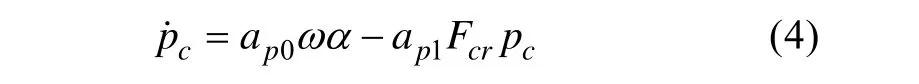
动力系统动力学方程［6］

2.2泵角执行机构模型

此外，以儿童在来生信念测量的总分为因变量，以2(父母宗教信仰组别)× 2(年龄：4～5岁、5～6岁)进行方差分析，结果发现，对于儿童来生信念测量的总分，年龄与父母宗教信仰组别交互作用不显著，父母宗教信仰组别(宗教信仰组：M=6.18，SD=3.61；无宗教信仰组：M=8.89，SD=2.98)主效应显著，F(1, 53)=8.20，p=0.006，η2=0.14。

泵角执行机构本身是一个闭环控制系统。其指令输入是转速控制器输出的控泵电压信号，它与斜盘角位置反馈电压形成电压误差； 误差经过幅度放大（比例控制）形成驱动伺服电机的电压指令。为了充分发挥电机的潜力，加快运动响应速度，该幅度放大环节可设置为带饱和的非线性环节； 电机驱动电路响应放大了的电压指令，形成PWM调制波驱动直流伺服电机； 电机转速对于该驱动电压的响应是惯性环节，电机的转速通过减速机构比例转化为斜盘角摆动角速度； 该摆动角速度通过一次积分，得到斜盘角位置并通过位置传感器形成反馈电压。变排量燃料泵及泵角执行机构的结构及实物如图2、图3所示。

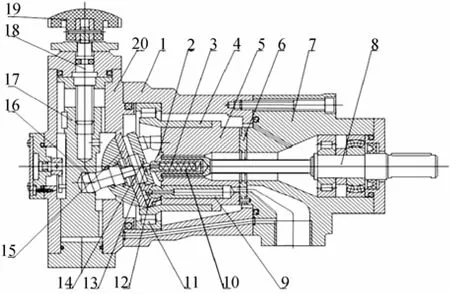
图2　变量泵结构图Fig. 2　Structure of a variable pump

图3　变量泵实物图Fig. 3　Picture of a variable pump

系统泵控电压至斜盘角传递函数可表达为

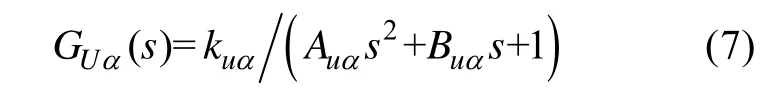
为简化分析过程，考虑到泵角过渡过程的小超调特征，使用惯性环节来替代上述2阶环节［7-8］，即系统泵控电压至斜盘角的传递函数可近似描述为

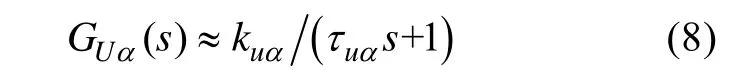
写成微分方程的形式为

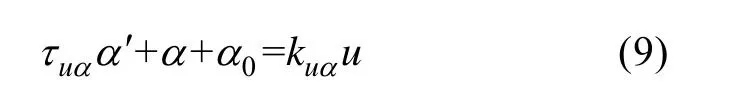
其中，0α为泵控电压为零时对应的稳态泵角。

3　控制算法

文中采用调节燃料泵的排量实现对涡轮机转速的控制。根据已建立的涡轮机动力系统模型，得到动力系统各个部分的控制框图如图4所示。

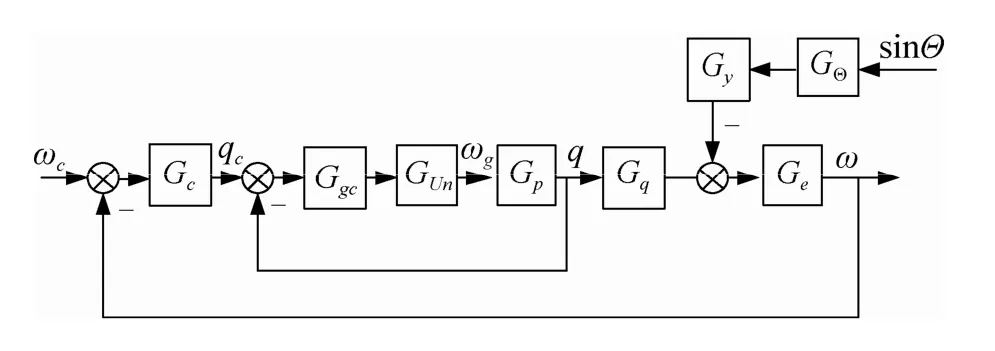
图4　涡轮机动力推进系统各部分控制框图Fig. 4　Control block diagram of turbine propulsion system

电机转速对于驱动电压的响应可近似为惯性环节

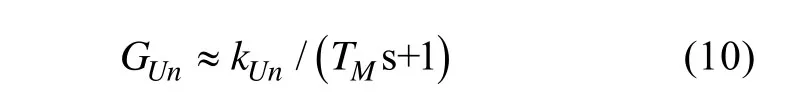
发动机流量对于泵排量的响应特性为

工作深度对于俯仰角的响应特性为

背压对于深度的响应特性为

发动机的传递函数可近似描述为

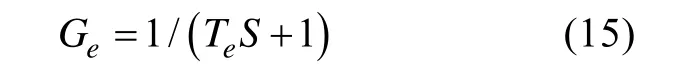
整个控制算法包括转速控制环和泵角位置控制环。转速控制算法采用比例积分环节

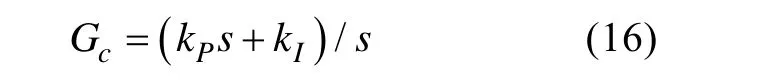
泵角控制算法采用比例环节

根据转速控制算法Gc，可由指令转速cω和反馈转速ω求得泵角位置控制指令qc。根据电机控制算法Ggc，可由泵角位置指令qc和泵角位置反馈q，从而控制泵角的位置，当航行器的俯仰角Θ不为0时，航行器做变深运动，为泵角位置指令的负反馈。由此可得，整个动力的控制方程为

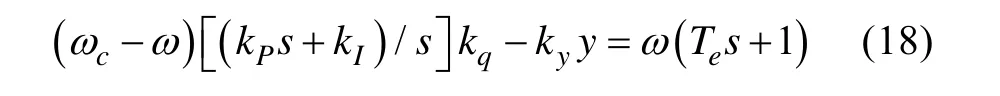
从而

因此发动机的转速

由上式可看出，转速对航深y和指令转速cω无静态误差。

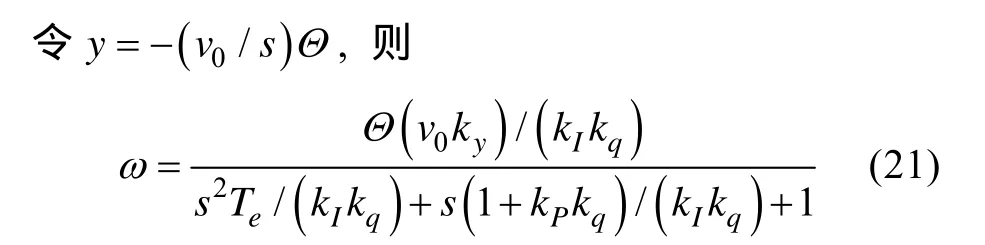
4　转速闭环控制器的设计

基于以上算法研制了以C8051f920为控制核心的转速闭环控制器，以实现接受上位机指令并根据指令驱动及控制变排量燃料泵直流电机的功能。硬件设计过程中充分考虑系统抗干扰的能力，以保证设计的可靠性及稳定性。软件方面，系统对涡轮机转速和燃料泵泵角位置的采样周期低于5 μs，并将ADC的转换数据累加32次求平均值以保证反馈信息的准确，泵角位置的控制周期0.1 ms，转速控制周期75 ms。其程序流程见图5。

5　仿真试验与分析

为验证该控制系统的可靠性和实用性，在新型水下热动力系统试验台上对其进行试验并对试验数据记录分析。

该试验台由实物分系统及模拟分系统构成。其中，燃烧室、涡轮发动机、推进器由数学模型代替； 实物分系统由燃料泵、燃料供给子系统、测控子系统、电力拖动实体及其他辅机组成。

试验系统设定在30 m定深启动，历经火药柱单独燃烧、药柱和燃料混合燃烧、燃料单独燃烧阶段，在0～12 s完成启动过程，发动机转速稳定至Ⅰ速； 在33～45 s完成恒速上爬过程，航深变至10 m； 在73～80 s完成恒深变速过程，发动机转速变至Ⅱ速； 在110～117 s完成恒深变速过程，转速变至Ⅰ速； 在149～173 s完成恒速下潜过程，航深变至50 m； 在200～206 s完成恒深变速过程，转速变至Ⅱ速。系统在后续过程中完成恒深变速、恒速变航深各2次，往复试验增加试验可信度。

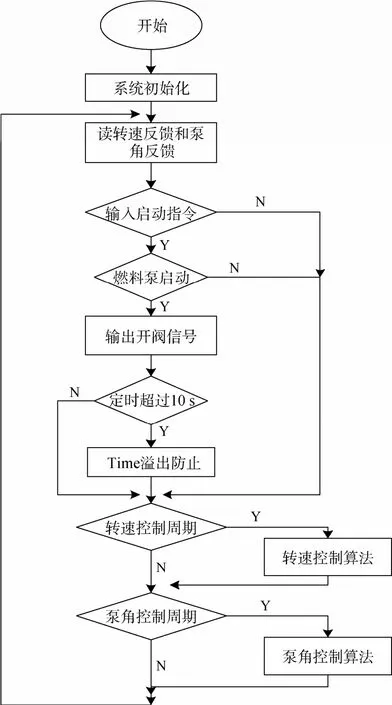
图5　转速闭环控制器程序流程Fig. 5　Program flow chart of closed-loop rotary velocity controller

上述半物理仿真试验过程中航深、燃料泵流量、燃烧室压力、发动机转速和推进器角速度随时间变化曲线见图6～图8，其中图7和图8纵坐标为当前时刻该参数与其最大设计值的相对值。

系统变工况可分为变速和变航深2个过程。对比图6、图7和图8可发现： 1）系统定航深变速（切换至高速或低速）时，燃料泵出口处流量会相应变化（增大或减小），燃烧室压力正比于燃料泵流量，转速调节过渡时间不大于7 s； 2）系统变航深（下潜或上爬）时，燃料泵出口处流量会相应变化（增大或减小），燃烧室压力正比于燃料泵流量，以补偿涡轮机出口背压的变化，确保发动机转速稳定不变； 3）系统变工况过程中，发动机转速最大偏差不超过20 r/min； 4）系统各个指标参数（燃烧室压力等）对于变速、变航深的响应，均不会发生超调。切换动作、下潜、上爬、变速以及系统稳态指标均合乎要求。

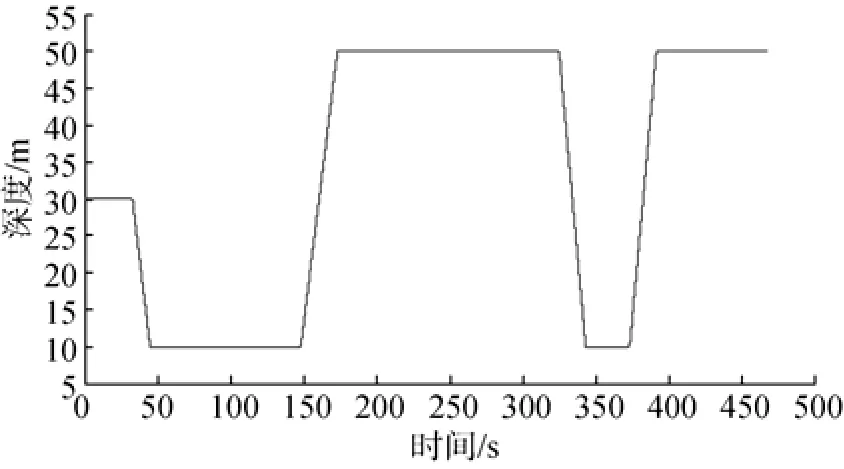
图6　航行器航深随时间变化曲线Fig. 6　Curve of depth versus time for an AUV

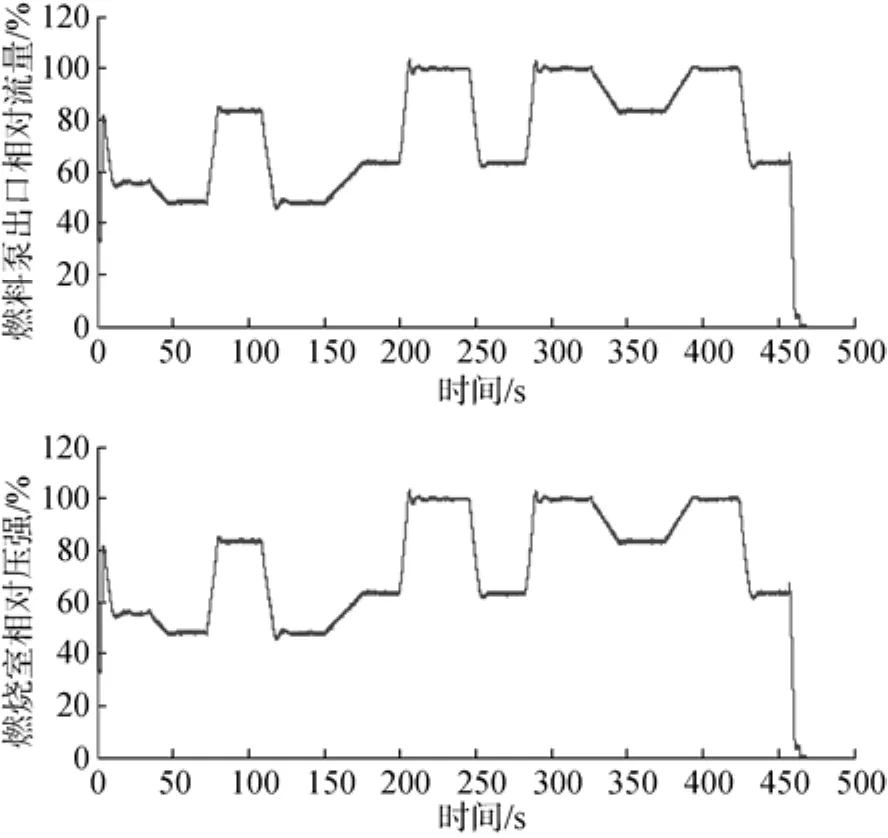
图7　燃料泵输出流量和燃烧室压力随时间变化曲线Fig. 7　Curves of fuel pump output flow and combustion chamber pressure versus time

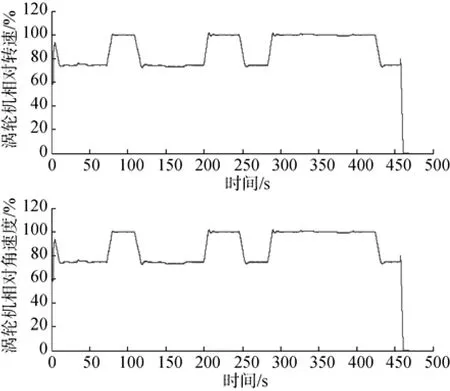
图8　发动机转速和推进器角速度随时间变化曲线Fig. 8　Curves of turbine rotary velocity and propeller angular velocity versus time

6　结束语

应用于高速水下航行器的开式涡轮机动力系统对工况敏感，文中采用了一种基于调节变排量燃料泵斜盘角的转速闭环控制策略，建立了涡轮机动力系统模型和变量泵泵角执行机构模型，设计合理的控制算法，并研制了以C8051为控制核心的转速闭环控制器。

半物理试验仿真结果表明，所建立的系统模型合理，所研制的控制器稳态精度高，动态性能良好，变工况时系统转速波动在合理范围之内，变速无超调，满足水下航行器涡轮机动力系统的应用要求。因为试验过程中的转速指令为模拟信号，变量泵斜盘角也是连续可调的，即每一个泵角位置对应着一个转速，所研制的转速闭环控制器已具备无级变速的能力。

［1］查志武，史小锋，钱志博. 鱼雷热动力技术［M］. 北京：国防工业出版社，2006.

［2］赵寅生. 鱼雷涡轮机原理［M］. 西安： 西北工业大学出版社，1995.

［3］石秀华，王晓娟. 水中兵器概论（鱼雷分册）［M］. 西安：西北工业大学出版社，2005.

［4］罗凯，党建军，王育才. 水下热动力推进系统自动控制［M］. 西安： 西北工业大学出版社，2005.

［5］李代金，张宇文，罗凯，等. 水下热动力推进系统的无级变速控制研究［J］. 西北工业大学学报，2009，27（2）：195-198.

Li Dai-jin，Zhang Yu-wen，Luo Kai，et al. Nonlinear Variable-Structure Control for Stepless Speed Changing of Underwater Heat-Engine Propulsion System［J］. Journal of Northwestern Polytechnical University，2009，27（2）： 195-198.

［6］罗凯，党建军，王育才. 水下涡轮发动机动力推进系统数学模型系统［J］. 交通运输工程学报，2006，6（2）： 35-38.

Luo Kai，Dang Jian-jun，Wang Yu-cai. Mathematics Model of Underwater Turbine Engine System［J］. Journal of Traffic and Transportation Engineering，2006，6（2）： 35-38.

［7］Hung J Y，Gao W B，Hung J C. Variable Structure Control：A Survey［J］. IEEE Trans on Industrial Electronics，1993，40（1）： 2-22.

［8］Bakker R，Annaswamy A M. Low-order Multivariable Adaptive Control with Application to Flexible Structures［J］. Automatic，1993，32（3）： 409-418.

（责任编辑： 陈曦）

A Closed-loop Rotary Velocity Controller for Underwater Turbine Propulsion System

LUO Kai，ZHANG Xue-lei，WANG Xiao-xin，LUO Xin
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

The open circle turbine propulsion system applied to high-speed autonomous underwater vehicle （AUV）has the outstanding characteristics of low gas consumption，large enthalpy drop and simple structure. But this system is sensitive to varying conditions. In this study，the closed-loop control strategy was adopted by adjusting the fuel pump angle to establish mathematical models of the open circle turbine propulsion system and the pump angle actuator. A reasonable control algorithm was designed. Based on the models and the algorithm，a closed-loop rotary velocity controller was developed. Thus，the stepless speed control of underwater turbine was achieved. Hardware-in-the-loop simulation result shows that the proposed controller can keep the system′s rotary velocity following the command velocity in varying conditions （variable depth or velocity）. The transition time of the rotary velocity regulation is less than 7 s，and the maximum deviation of rotary velocity is less than 20 r/min. The combustion chamber pressure overshoot is less than 5%，which ensures the security of the system. The controller may effectively support the implementation of new guidance law of an AUV.

autonomous underwater vehicle（AUV）； open circle turbine； closed-loop control； controller； stepless speed

TJ630.32； TK323

A

1673-1948（2015）01-0044-05

2014-09-27；

2014-11-10.

罗凯（1972-），男，教授，博士生导师，主要研究方向为水下动力系统、液压系统以及自动控制.