假海试验设施复杂内流场仿真

董明阳，王　云，段　浩

（中国船舶重工集团公司 第705研究所昆明分部，云南 昆明，650118）

假海试验设施复杂内流场仿真

董明阳，王云，段浩

（中国船舶重工集团公司 第705研究所昆明分部，云南 昆明，650118）

为了详细、直观、准确地描述发射过程中空气涡轮泵发射装置在假海试验设施内部流场的压力场、速度场分布，建立了在发射试验过程中假海试验设施内流场的数学模型，并运用Fluent的动网格技术对该模型进行了数值仿真。仿真结果显示了假海试验过程中各个阶段的压力场和速度场的分布情况，为试验设计提供参考。依照仿真结果对试验过程中出现的一些现象做出解释。根据假海内部流场的仿真结果对流场的恢复情况进行预测，为连续发射时间间隔的确定提供理论依据。

空气涡轮泵发射装置； 假海； 内流场； 压力场； 速度场； 动网格

0　引言

假海试验设施是支撑大深度雷弹发射关键技术研究的基础试验设施的主要组成部分，可以将不同口径、多种类型发射系统集成在一个假海中，为水下多种武器发射提供大深度模拟水深的发射试验环境。通过假海试验设施可进行诸多发射装置研发过程中必不可少的相关试验研究，相关的试验结果及时反馈到研制过程中，可以提高发射装置可靠性和安全性，有效降低系泊试验、实航试验风险，减少试验次数，缩短研制周期。

对假海试验设施内部流场进行数值仿真，可以得到发射过程中假海筒体内部流场的压力、速度分布以及波动情况，同时还可以探究假海试验设施内的流场扰动对发射装置性能测试的影响，为发射装置的性能测试试验设计提供参考，使试验设计更加合理、准确。文中以空气涡轮泵发射装置在假海试验设施上的发射试验过程为研究对象［1］，建立相应的流场数学模型，利用Fluent软件的动网格技术对该模型进行数值仿真［2-3］。

1　模型的建立

假海内部流体的运动主要有以下特点： 一是从武器发射过程来看，整个假海设施在水平面内上下对称，由于受导轨的束缚，鱼雷的运动轨迹一直保持在穿过中心线的水平面内。由于武器在水中的负浮力较小，加之武器的运动被约束在导轨架内，为了便于研究，可以忽略重力的影响，从而将其简化为2D流动模型； 其次，假海内部的流体流动是在一个循环封闭的系统中进行的，由于混流泵有良好的敞水性能，在此忽略水泵叶片对流体流动的阻碍作用，水泵在整个假海中可视作畅通的流道。空气涡轮泵发射装置在其中起动力源作用，因此可将水泵的入口、出口作为整个模型闭环的初始、终端边界条件。

假海筒体内部流体的流动满足质量守恒定律、动量守恒定律，根据这些定律可以建立相应的假海筒体内部流体的纳维-斯托克斯方程［4］。

1.1不可压纳维-斯托克斯方程

将假海筒体内流体均视为不可压缩流体，忽略流体温度变化，其运动方程满足如下形式的纳维-斯托克斯方程

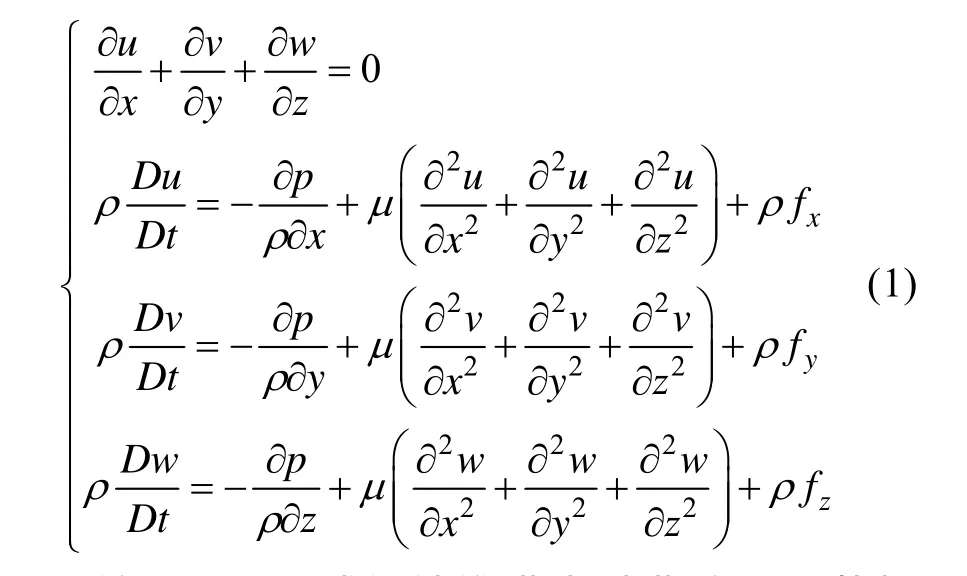
该不可压形式的纳维-斯托克斯方程是从标准的可压纳维-斯托克斯方程得到的。将标准方程中的密度令为常数，再经过一定过程的推导就可以得到如上所示的不可压纳维-斯托克斯方程。

式（1）中： u，v，w，p为待求解流场变量，分别表示流场在x方向（发射管轴线方向）、y方向、z方向的速度以及压力（y，z与x构成符合右手定则坐标系）； ρ，fx，fy，fz为已知量，分别表示流场内流体密度以及流体质量力在x，y，z方向上的分力。对上述方程求解的目的就是为了得到随时间t以及位置坐标x，y，z变化时，u，v，w，p的变化情况，从而得到整个流场的速度、压力分布。

纳维-斯托克斯方程比较准确地描述了实际的流动，由于其形式较为复杂，实际上只有极少情况可以求出精确解，故选择通过数值仿真来求解。

1.2鱼雷弹道模型

鱼雷在发射过程中主要受到重力、迎面阻力、管壁摩擦力、尾部推力［5］影响，其受力如图1所示。

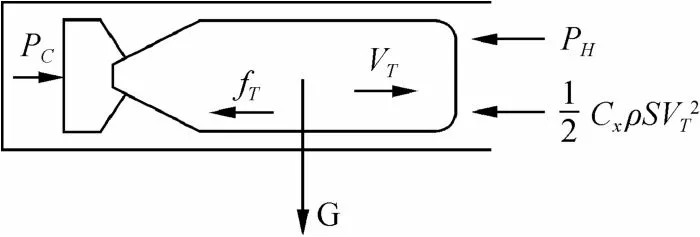
图1　鱼雷发射过程中的受力情况Fig. 1　Force schematic on a torpedo during launching process

把运动的海水与鱼雷视为一个整体，根据牛顿第二定律，其运动方程为

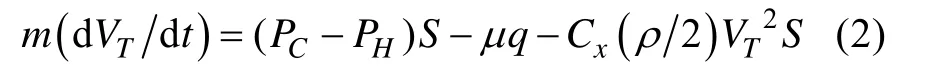
式中： m为鱼雷及其附着水质量； PT为鱼雷尾部压力； PH为鱼雷头部压力，即外部海水静压；Cx为迎面阻力系数； S为鱼雷浸湿面积； μq为管壁摩擦力； ρ为流体（水）密度； VT为当前时刻鱼雷速度； t为发射过程中的时间。

鱼雷出管后在假海筒体内的运动过程中主要受力为导轨摩擦力、迎面阻力、水的粘性阻力等； 鱼雷在进入回收管的运动过程中受力为鱼雷前后压差阻力、迎面阻力、管壁摩擦力、水的粘性阻力等。

1.3假海试验设施模型

鉴于假海试验设施上下对称的结构，以假海筒体中心水平切面为研究对象，建立2D模型。假海试验设施整体结构复杂，文中对其进行简化处理，其模型如图2所示（俯视图）。其中左下角连接2根大小管道的圆形装置为空气涡轮泵发射装置的水泵，简化后视水泵为可流通管道，将水泵的出口作为假海模型的入口边界条件、水泵入口作为假海模型的出口边界条件。对水泵作简化后模型如图3所示。根据流体的连续性方程，可得假海模型的入口、出口的质量流量是一致的。

2　流场数值仿真

2.1网格划分

对图3所示的模型进行网格划分即可得到其网格模型。在划分网格时，由于发射管与鱼雷之间的间隙很小，尤其是水密环处，不宜进行均匀划分。因此，文中采用了划分混合网格的方法，网格模型如图4所示。计算中生成的网格数约为11万个。

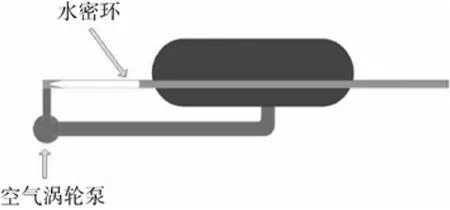
图2　假海试验设施2D模型Fig. 2　Two-dimensional model of false sea test facility

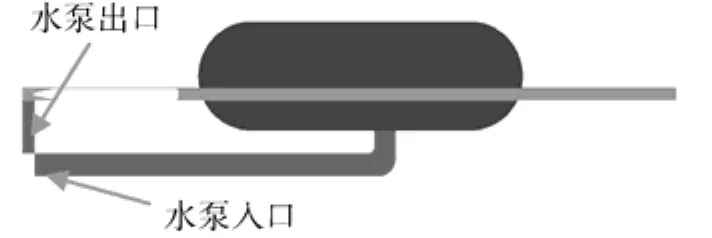
图3　简化后假海2D模型Fig. 3　Simplified two-dimensional model of false sea test facility

图4　假海模型网格生成图Fig. 4　Mesh of false sea test facility

2.2动网格原理

在Fluent中，除了动网格功能能够描述计算区域瞬态运动外，还有滑移网格能描述计算区域的运动。滑移网格最大的优点就是在计算区域的运动过程中，网格能一直保持很高的质量，避免了因为动网格更新过程中网格质量差导致数值解误差较大的后果。

由于在假海模型中安装有导轨，导轨将鱼雷的运动轨迹约束为仅沿轴线方向运动。同时鱼雷两侧间隙非常小（尤其是水密环处），如果采用网格重构法进行网格的更新可能很难保证网格质量。因此，为了保证鱼雷运动过程中较高的网格质量，文中综合采用滑移网格［5］和动网格铺层法实现流场仿真的动网格处理。

2.3数值仿真

为了更真实地对假海筒体内的流场进行仿真，将试验中所获得的鱼雷速度数据经过拟合后作为该仿真中鱼雷的速度输入。同时将试验中采集的涡轮泵出口处产生的压力数据作为该仿真的边界条件，并将假海内环境压力设置为0.3 MPa （即30 m水压）。借用的鱼雷速度曲线、水泵的抛射压力输出曲线分别如图5、图6所示［6］。

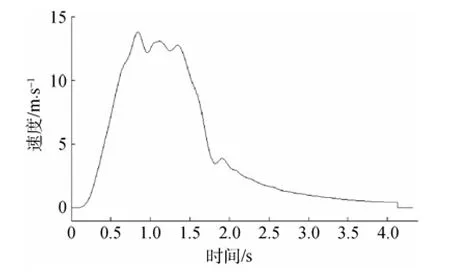
图5　速度曲线Fig. 5　Curve of velocity curve versus time

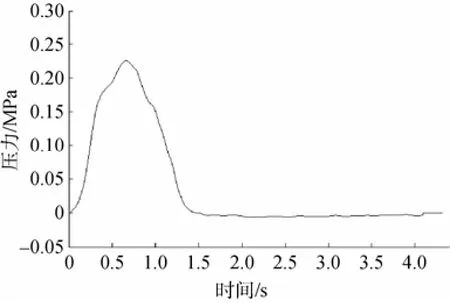
图6　压力曲线Fig. 6　Curve of pressure versus time

初始化模型并进行仿真计算。为了更好地观察流场随着鱼雷运动的变化，可在计算开始之前设置相关流场参数的动画以方便观测整个过程流场变化情况。计算收敛后，分别保存模型和计算结果。

3　仿真结果及分析

Fluent中提供的后处理功能，用以对计算结果进行分析处理，也可以用可视化的方法对流场的空间分布予以显示。由于该流场仿真属于非定常流动，需要对几个特定流场进行分析，因此将各个典型时刻的流场图片分别提取进行分析。

3.1仿真结果

图7～图18为通过仿真得到的在发射试验过程中各个时刻的流场分布。

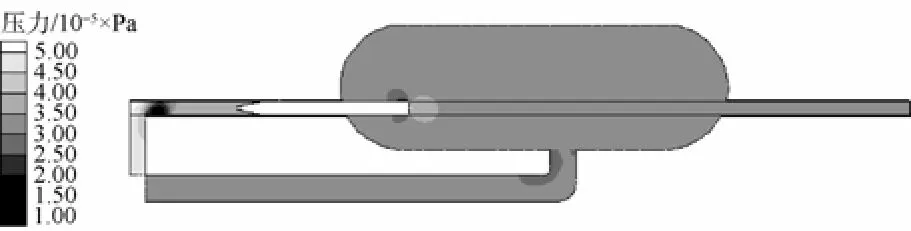
图7　压力云图(t=0.66 s)Fig. 7　Contour of pressure when time is 0.66 s

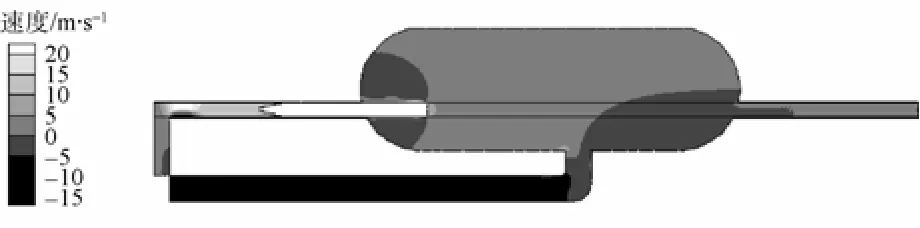
图8　速度云图(t=0.66 s)Fig. 8　Contour of velocity when time is 0.66 s

图9　压力云图(t=0.92 s)Fig. 9　Contour of pressure when time is 0.92 s

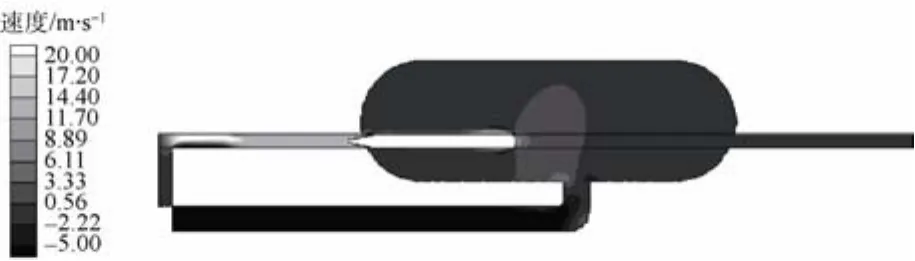
图10　速度云图(t=0.92 s)Fig. 10　Contour of velocity when time is 0.92 s

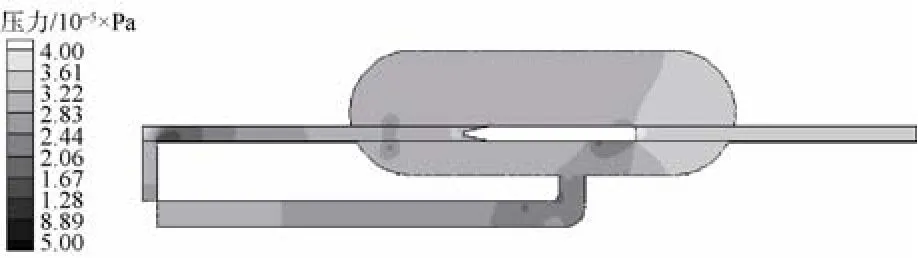
图11　压力云图(t=1.3 s)Fig. 11　Contour of pressure when time is 1.3 s

图12　速度云图(t=1.3 s)Fig. 12　Contour of velocity when time is 1.3 s

图13　水密环处压力云图(t=0.66 s)Fig. 13　Contour of pressure around watertight ring when time is 0.66 s

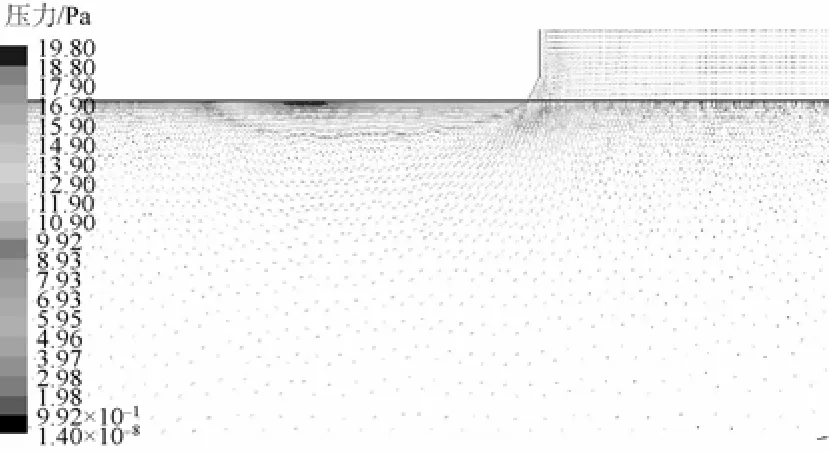
图14　鱼雷头部区域压力云图(t=1.3 s)Fig. 14　Contour of pressure around the head of torpedo when time is 1.3 s

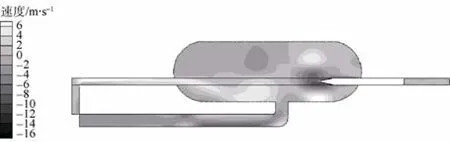
图15　速度云图(t=3.2 s)Fig. 15　Contour of velocity when time is 3.2 s

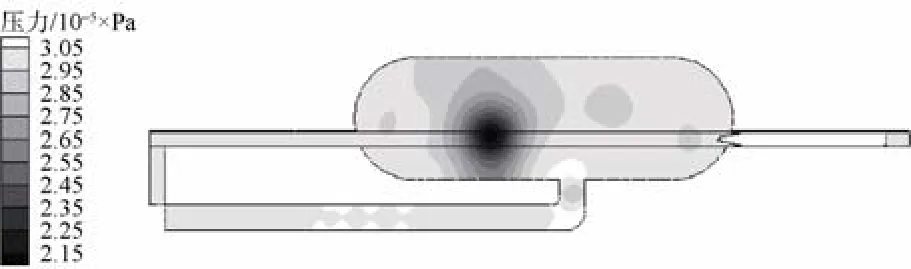
图16　压力云图(t=5.82 s)Fig. 16　Contour of pressure when time is 5.82 s

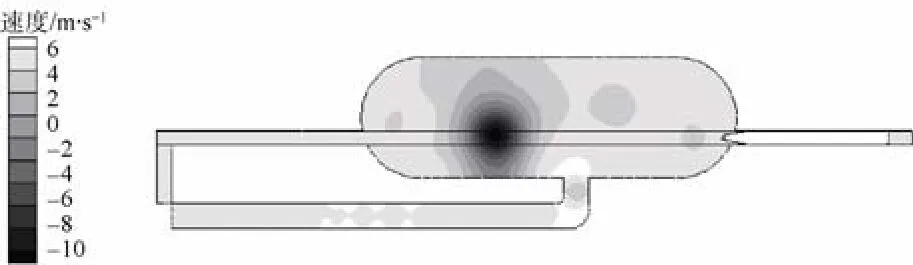
图17　速度云图(t=5.82 s)Fig. 17　Contours of velocity when time is 5.82 s

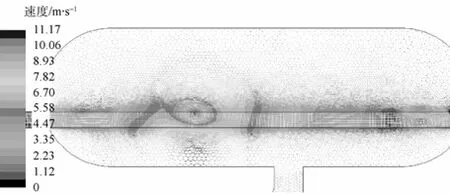
图18　速度矢量图(t=5.82 s)Fig. 18　Diagram of velocity vector when time is 5.82 s

3.2结果分析

从0.66 s和0.92 s时刻的压力云图可以看出，水泵产生的压力从水泵出口处到鱼雷尾部逐级递减，且在流体从后端管道进入发射管的过程中，由于注疏水阀的作用导致流动过程中产生了较大的压力损失。鱼雷进入假海筒体内对流体产生了瞬间挤压作用，筒体内压力瞬间上升。从水密环处的压力分布云图可以看出，涡轮泵输入的压力在水密环处迅速降至环境压力以下，即产生了负压。在距离水密环较远的地方，压力又逐渐恢复到假海筒体内环境压力。从水密环两端明显的压降可以说明水密环的存在可以减少涡轮泵输入压力的损失，有利于鱼雷充分加速。

根据各个时刻流场速度云图显示，在发射过程开始阶段，水流只是在管道和靠近管道的区域循环，假海内远离管道区域的流动不明显。随着发射过程的推进，流场波动逐渐蔓延至整个筒体。可以明显看出，筒体内流体对筒体右侧（循环水道所在的一侧）冲击远强于左侧，这是由于循环水道位于筒体右侧的不对称结构造成的。从图16所示的压力云图可以看出，当鱼雷停止运动一段时间后，大部分区域均已恢复至环境压力，但由于漩涡（如图17、图18所示）的原因，假海筒体后方区域出现了较大的低压区，漩涡产生的载荷导致筒体右侧有较大的高压分布区域。在整个试验过程中，流体对筒体右侧的持续冲击可能会对筒体右侧产生疲劳损伤，为了保证试验的长期正常进行，对假海筒体右侧尝试进行加强是延迟假海使用寿命的一种方法，同时确保假海基座的稳定坚固。从图12还可以看出，鱼雷在假海内运动时，筒体内流体的流动很剧烈，尤其在鱼雷右侧，通过图16所示的鱼雷右侧流场速度矢量图可以看出，鱼雷右侧形成了大强度的漩涡，在鱼雷右侧产生了比较大的压力，会导致两侧导轨受力不一致。此外，鱼雷右侧的压力波动引起鱼雷和导轨之间摩擦力的变化，使鱼雷运动过程中产生速度震荡，试验测试结果也印证了这一点。

通过观察各个时刻压力云图分布发现，假海筒体后端（靠近发射管一端）左侧压力波动较小，相对稳定，可作为试验中传感器的布置位置，这有利于提高试验数据采集的准确性，减小干扰。

鱼雷在3.72 s时停止运动，图16、图17为鱼雷停止运动约2.1 s后假海内部流场分布情况。从该时刻的速度云图可以看出，除了循环水道出口左侧有局部漩涡导致速度较高外，其他地方的最高速度已降至3 m/s以下，而发射过程中流场局部速度最高达到20 m/s，因此可认为现在筒体内大部分区域的速度已降到发射过程中最大速度的15%以下。仿真结果还可以指导试验方案的制定，比如，2次发射间隔时间的确定。在规定了最大允许的残余速度下，根据上述的仿真结果便可确定相应的间隔时间。比如，若以筒体内水流速度普遍降低到最大峰值的15%以下作为可进行第2次发射的标准，则发射完毕直至鱼雷停止约2.1 s后，便可进行下一次发射。

4　结 论

文中所建立的假海发射试验过程中的流体流动模型，利用Fluent软件的动网格技术对其进行了数值仿真。由仿真结果可以得到以下结论：

1）依照仿真结果可以得到发射过程中发射管内压力分布的变化以及水密环对压力分布的影响，验证了水密环的重要性，也为水密环的间隙设计提供了理论依据；

2）对试验过程中出现的大强度涡流分析发现，强度大的涡流会引起假海筒体产生不对称的压力波动，同时还会导致鱼雷在导轨束缚下摩擦力的剧烈变化，从而产生速度震荡；

3）根据发射过程中压力分布情况，可以发现假海筒体左边靠近发射管后端区域的压力波动较小，是进行压力传感器布置的理想部位；

4）根据假海内部流场的仿真结果，可以预测流场恢复稳定并逐渐趋于静态的时间，为连续2次发射时间间隔的确定提供了理论依据。

［1］刘家铨. 潜艇鱼雷发射装置概论［M］. 哈尔滨： 哈尔滨工程大学出版社，2003.

［2］韩占忠，王敬，兰小平. Fluent流体工程仿真计算实例与应用［M］. 北京： 北京理工大学出版社，2004.

［3］隋洪涛，李鹏飞，马世虎，等. 精通CFD动网格工程仿真与案例实战［M］. 北京： 人民邮电出版社，2013.

［4］龙天渝，苏亚欣，向文英，等. 计算流体力学［M］. 重庆：重庆大学出版社，2007.

［5］宋保维，黄海. 气动不平衡式鱼雷发射器内弹道流场仿真研究［J］. 鱼雷技术，2008，16（2）： 46-49.

Song Bao-wei，Huang Hai. Simulation of Inner Trajectory Flow Field for Pneumatic Imbalance Torpedo Launcher［J］. Torpedo Technology，2008，16（2）： 46-49.

［6］ANSYS Inc. Fluent User′s Guide［M］. United States： ANSYS Inc，2003.

（责任编辑： 许妍）

Simulation on Complicated Inner Flow Field in False Sea Test Facility

DONG Ming-yang，WANG Yun，DUAN Hao
（Kunming Branch of the 705 Research Institute，China Shipbuilding Industry Corporation，Kunming 650118，China）

To obtain a detailed，intuitive and accurate description of the pressure field and velocity field distribution of inner flow field in false sea test facility for an air-turbine pump launcher during launching，a mathematical model of inner flow field in false sea test facility is established，and simulation is conducted by using dynamic mesh of FLUENT. The results illustrate the distributions of pressure field and velocity field of inner flow field in false sea test facility at every stage of the launching process，which may be taken as a reference for test design. In addition，explanation is given for the phenomena appeared during the launching test by considering the simulation results of false sea test. And the recovery state of the inner flow field is predicted according to the simulation results to provide a theoretical basis for determining time interval between two continuous launching.

air-turbine pump launcher； false sea； inner flow field； pressure field； velocity field； dynamic mesh

TJ635

A

1673-1948（2015）01-0066-05

2014-12-02；

2014-12-17.

董明阳（1989-），男，在读硕士，研究方向为鱼雷发射技术.