涡轮机转子系统弹性环刚度特性有限元仿真分析

李日朝

（中国船舶重工集团公司 第705研究所，陕西 西安，710075）

涡轮机转子系统弹性环刚度特性有限元仿真分析

李日朝

（中国船舶重工集团公司 第705研究所，陕西 西安，710075）

涡轮机转子系统的弹性支撑刚度是调整和控制临界转速的关键。该文采用有限元法建立了弹性环刚度计算模型，分析了弹性环自身各个结构参数、涡动角以及装配间隙等参数对弹性环刚度的影响。通过试验测试，验证了应用有限元法计算弹性环支撑刚度的可行性和精确性。试验结果表明，弹性环刚度设计需主要考虑的参数为凸台数目、壁厚、宽度以及装配间隙，为弹性环的动力学设计提供依据。

涡轮机； 转子系统； 弹性环； 刚度； 有限元方法

0　引言

在旋转机械中，弹性阻尼支撑是降低常规振动级和动态压力的有效方法之一。弹性支撑在系统中表现出2种主要功能： 一是降低转子支撑的刚度，改变弹性动态机组的性能，同时降低系统固定频率，使工作转速远离临界转速； 二是吸收机组动态系统的振动能量，并转化为热能，弹性支撑抑制了系统的振动幅值、动态负载和动态压力的增长［1-3］。

弹性环属于径向式弹性支撑，内、外表面分别设有数目相同、沿圆周交错均布的若干个径向凸台的环形弹性元件，内表面凸台与轴承外圈相接触，外表面凸台与轴承座的内环面相接触，其结构形式如图1所示。弹性环具有良好的刚度特性，与滚动轴承组合后，支撑总刚度减小，采用不同结构的弹性环就能够调节和控制转子临界转速，使转子工作转速远离临界转速。同时，弹性环具有阻尼作用，在变形及恢复过程中吸收部分振动能量，可以大大减小转子的最大振幅，使转子平稳通过临界转速，同时可以减小轴承动压力，实现滚动轴承的高速化。

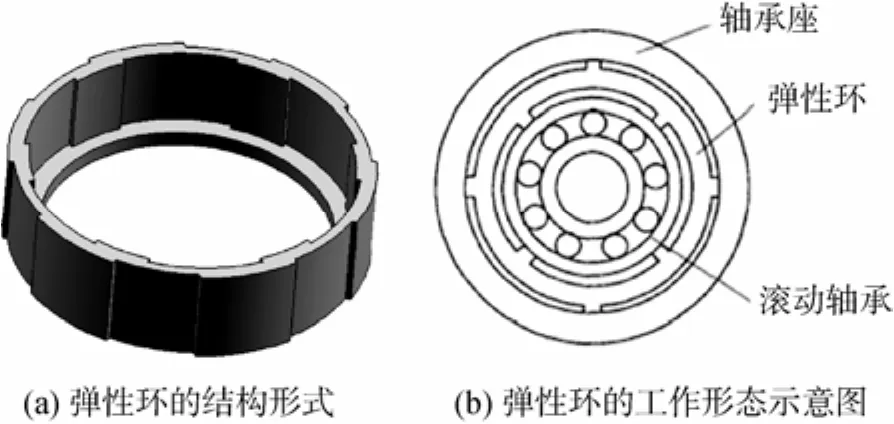
图1　弹性环支撑结构示意图Fig. 1　Schematic of support structure of an elastic ring

弹性环的刚度是转子支撑系统中一个非常重要的设计参数，其数值大小直接影响转子系统的临界转速。常用的求解弹性环刚度的方法有近似的解析方法和精确的数值法等。近似解析法不能精确地得到弹性环的刚度值，也无法计算弹性环的应力分布等强度特性［2］； 而精确的数值法对于结构复杂的弹性环难以适用，不能充分考虑凸台高度、宽度等结构参数对其刚度的影响。

文中采用有限元法计算弹性环的径向刚度，计算中根据弹性环的具体结构特点建立有限元模型，施加合理的边界条件，并采用非线性接触的方法对刚性环在径向力下的位移进行求解。

1　弹性环刚度计算

1.1有限元法相关描述

有限元法是一种求解复杂对象方程的方法，在分析受到径向载荷挤压的过程中，弹性环和轴承以及轴承座之间不可避免地会出现动态接触。而转子的自重、动不平衡响应以及突加不平衡响应等边界外力都是会引起动态接触的接触力，并且任意2个相互接触的体或者面都形成面接触对，这些接触对由“接触面”和“目标面”组成。接触问题存在2个较大的难点： 第一，在求解问题之前，通常无法预知接触区域，当材料、载荷或边界条件等因素发生变化时，接触面与目标面会突然接触或者突然分开，导致刚度非线性变化； 第二，多数接触问题中都存在摩擦作用，摩擦的响应可能是杂乱的，使求解难以收敛。此外为了阻止接触表面相互穿透，这2个表面之间必须建立一个关系。这些难点使得接触问题处理起来比较复杂和困难，不仅要处理搜寻接触区域的问题，还要处理非线性的求解问题。此外，还要考虑目标面和接触面之间在变形时互相穿透和摩擦滑动的现象。

根据ANSYS中各单元的特性，在建模中弹性环单元取SOLID95，接触单元取TARGE170和CONTA174。

SOLID95单元是SOLID45单元（3D 8节点）的高阶形式，该单元可以模拟不规则形状，同时不会降低计算的精确性； 此外，该单元偏移形状的兼容性较好。SOLID95单元具有20个节点，每个节点定义有3个自由度（分别为X，Y和Z方向），本单元具有提高计算蠕变、塑性、应力刚度、辐射膨胀、大变形以及大应变的能力，而且能够提供不同的输出项。

一般情况下，刚体表面总是指定为目标面，柔体表面为接触面［2］。用CONTA174单元模拟接触面，该单元是3D 8节点面接触单元，用于表示由其所定义的可变形表面与3D“目标面”之间的接触与滑动。

TARGE170用来表示接触对中的目标面，与覆盖在实体、壳或线性单元表面的接触单元相接触。该目标表面离散为一系列目标分单元，并通过设置共享实常数使之与相关的接触表面配对。

1.2弹性环有限元模型的建立

以设计的3种不同结构尺寸的弹性环为例，分析各个结构参数对其刚度的影响，弹性环的结构参数如表1所示。

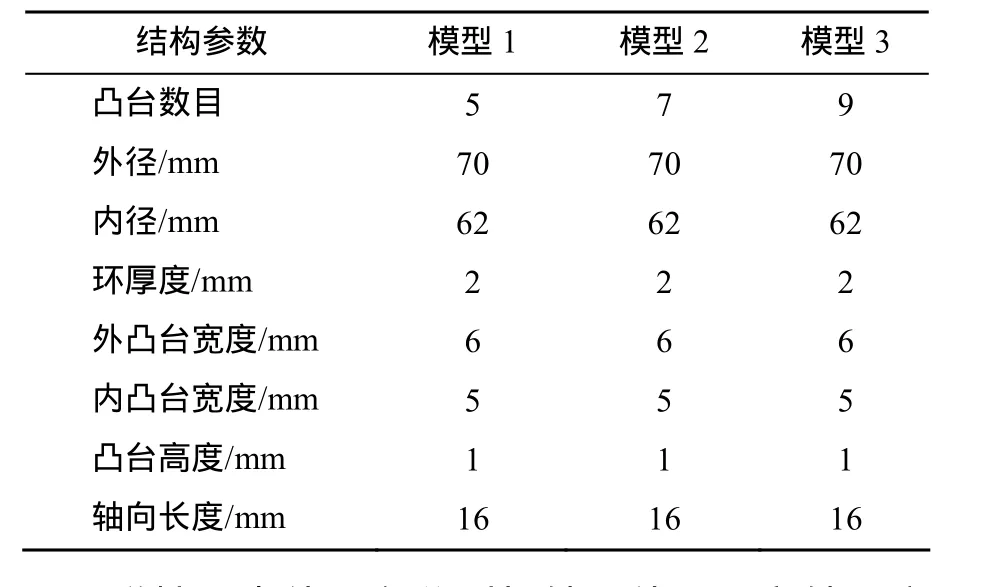
表1　弹性环结构参数Table 1　Structural parameters of an elastic ring

弹性环内外凸台分别与轴承外环面和轴承座内环面相接触，接触面受力分布非常复杂，所以在弹性环有限元模型的内侧建立一个与其相邻的刚性环来模拟轴承外环面，刚性环外环面与弹性环内凸台表面建立接触单元。同样地，在弹性环模型的外侧建立一个刚性环来模拟轴承座内环面，在这2 个面之间建立接触单元。

在建立弹性环的有限元模型中，使用的材料及材料属性如表2 所示。

表2　弹性环使用材料及材料属性Table 2　Material and material properties of an elastic ring

弹性环及2个刚性环在有限元软件平台下采用SOLID95单元建立有限元模型，对于接触部分，可以直接应用有限元软件中提供的3D面接触单元［2］。弹性环和刚性环的有限元模型如图2所示，其中刚性环的模型两端面都带端封，这样可以限制弹性环的轴向位移。图3所示为弹性环的有限元计算模型。

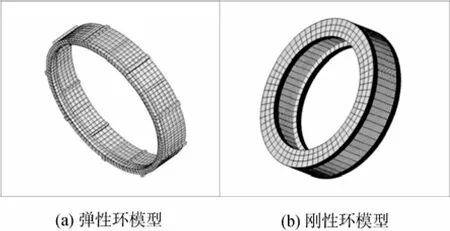
图2　弹性环和刚性环的有限元模型Fig. 2　Finite element models of an elastic ring and a rigid ring

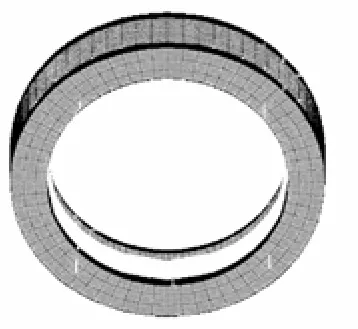
图3　弹性环有限元计算模型Fig. 3　Finite element calculation model of elastic ring

图4　弹性环位移场示意图Fig. 4　Schematic of dis-　 playcement field　 of an elastic ring

1.3弹性环有限元模型的边界条件

在计算弹性环径向刚度系数时，为了模拟弹性环支撑的真实边界条件，根据弹性环的结构特点，约束弹性环和内刚性环的轴向移动和各个方向的转动，并假定外刚性环固定。在内刚性环面上施加Y方向的径向力Fr，求出弹性环的位移量δr模拟转子的位移。由公式Kr：Kr=Fr/δr确定弹性环的径向刚度。计算弹性环的位移场见图4。

2　弹性环刚度随涡动角的变化

假定转子在某一偏心率下作稳态同步涡动，由于弹性环是周期对称结构，相邻2个内（外）凸台之间的夹角2π/m（m为单侧凸台数）对应一个涡动周期，在这个周期内，弹性环的刚度会随着涡动角的变化而变化。

在计算弹性环刚度时，假设涡动角的起始位置正对着内凸台，分别计算3个弹性环在1个周期内不同位置处的刚度，计算结果见表3和图5。

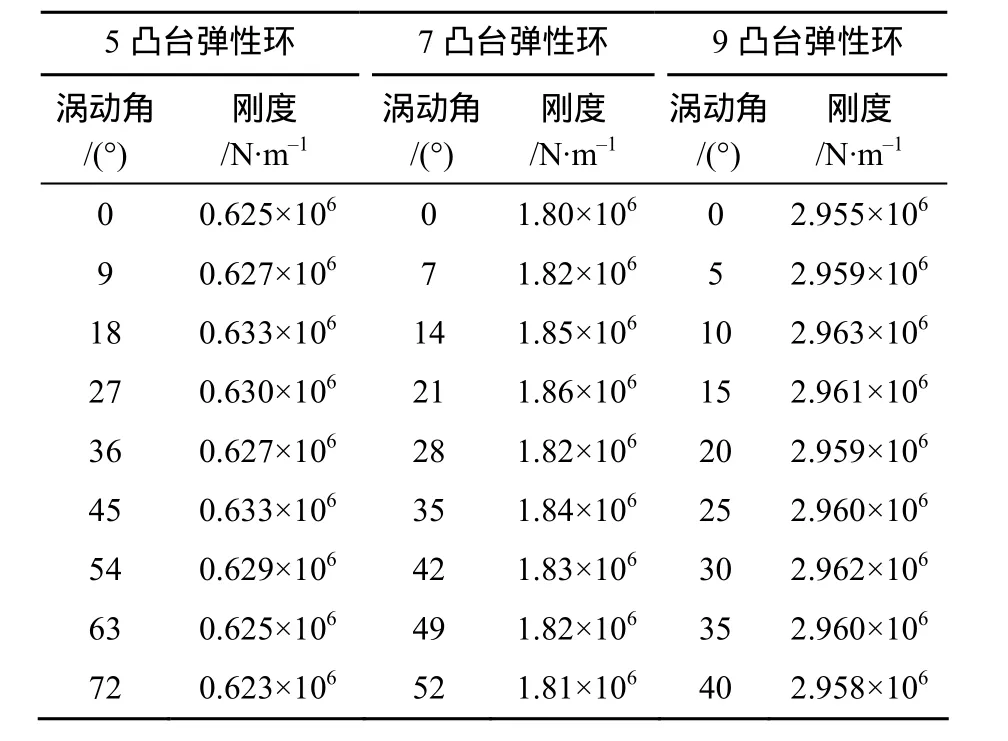
表3　不同凸台数目弹性环刚度随涡动角的变化Table 3　Change of elastic ring rigidity with whirling angle for different boss number

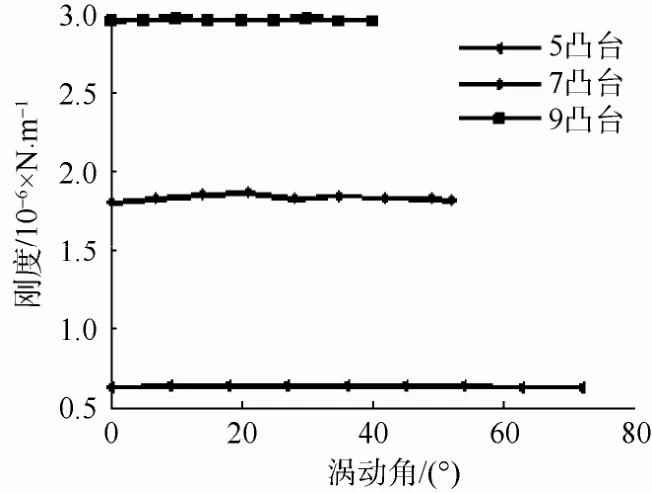
图5　不同凸台数目弹性环刚度随涡动角的变化规律Fig. 5　Curves of elastic ring rigidity versus whirling angle for different boss number

由图5可以看出，弹性环在1个结构周期不同位置处的刚度变化不大，取1个周期内各个涡动角对应的刚度平均值作为弹性环的刚度，可以得到3种不同凸台数的弹性环刚度如表4所示。

3　各结构参数对弹性环刚度的影响

3.1凸台数目对弹性环刚度的影响

运用所建立的计算模型，仅改变凸台数目，其他参数保持不变，分析弹性环的凸台数目对其刚度的影响，得出弹性环的刚度随凸台数目的变化规律如图6所示。

表4　不同凸台数目的弹性环刚度Table 4　Rigidity of elastic ring with different boss number

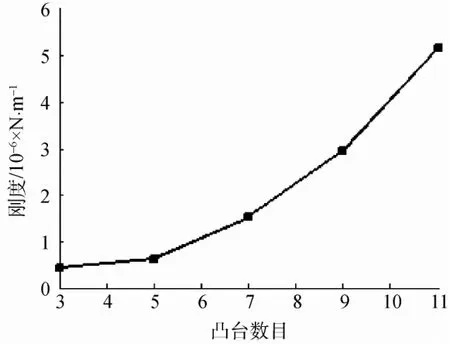
图6　弹性环刚度随凸台数目的变化规律Fig. 6　Curve of elastic ring rigidity versus boss number

由图6可知，随着凸台数目的增加，弹性环刚度非线性增大，且凸台数目愈多，弹性环刚度增大速度越快，11凸台弹性环的刚度是3凸台弹性环刚度的25倍，变化幅度较大。

3.2凸台宽度对弹性环刚度的影响

运用所建立的计算模型，以7凸台弹性环为例，分析弹性环的凸台宽度对其刚度的影响，仅改变凸台宽度，其他参数保持不变，得出弹性环的刚度随凸台宽度的变化规律如图7（a）所示。

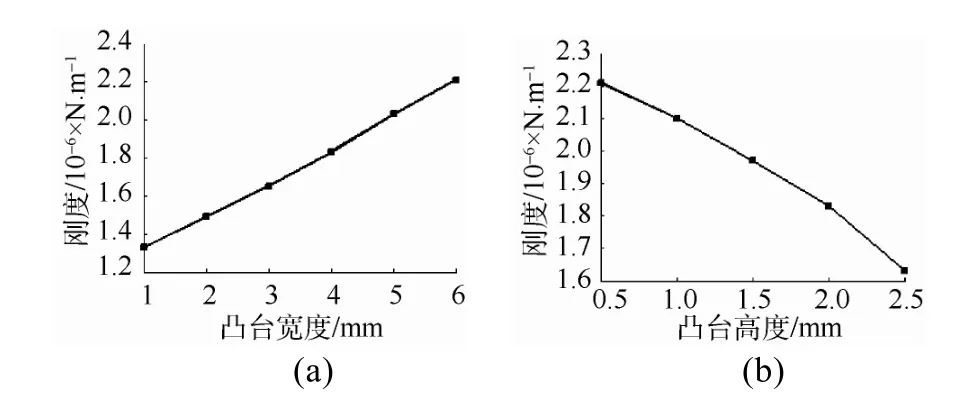
图7　弹性环刚度随凸台宽度和高度的变化规律Fig. 7　Curves of elastic ring rigidity versus boss width and height

由图7（a）可以看出，随着凸台宽度的增大，弹性环刚度基本呈线性增加，宽度每增加1 mm，刚度约增加0.2×106N/m。

3.3凸台高度对弹性环刚度的影响

与计算凸台宽度对弹性环刚度的影响类似，仅改变凸台高度，其他结构参数保持不变，计算凸台高度对弹性环刚度的影响，得出弹性环刚度随凸台高度变化的规律如图7（b）所示。

由图7（b）可以看出，随着凸台高度的增加，弹性环刚度呈非线性减小，且凸台高度越大，刚度减小速度越快。

3.4弹性环厚度对弹性环刚度的影响

仅改变弹性环厚度，其他结构参数保持不变，分析环厚度对其刚度的影响。刚度随弹性环厚度变化的规律如图8（a）所示。

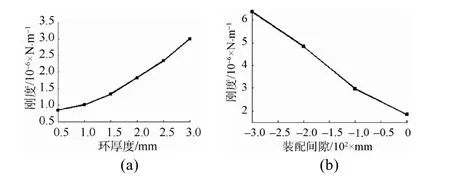
图8　弹性环刚度随弹性环厚度和装配间隙的变化规律Fig. 8　Curves of elastic ring rigidity versus thickness and fit clearance

由图8（a）可以看出，随着环厚度的增加，弹性环刚度非线性增加，且增大速度越来越快。

3.5装配间隙对弹性环刚度的影响

如果弹性环和轴承座的装配尺寸发生变化，接触面的接触方式就会发生变化，从而导致凸台的有效接触面积发生变化，对弹性环的刚度也会产生一定的影响。

以7凸台弹性环为例，运用所建立的弹性环有限元模型，通过改变弹性环和轴承座内环面的配合间隙，计算配合间隙对弹性环刚度的影响。弹性环刚度随装配间隙变化规律如图8（b）所示。

由图8（b）可以看出，随着弹性环与外刚性环装配间隙改变，弹性环的刚度变化较大。因为弹性环和刚性环为过盈配合时，弹性环存在预变形，使得弹性环受力时的变形量减小，进而导致弹性环刚度变大。配合间隙越小，弹性环系统的径向刚度越大。

4　试验验证

4.1测试原理

该测试结构将弹性环通过间隙配合套在轴头外，通过加载拉马对弹性环施加拉力，并通过拉力传感器来记录拉力的变化，而在弹性环的正上方布置电涡流位移传感器来记录弹性环在不同拉力下的位移，之后再对得到的数据进行分析总结。试验台的结构示意图如图9所示。

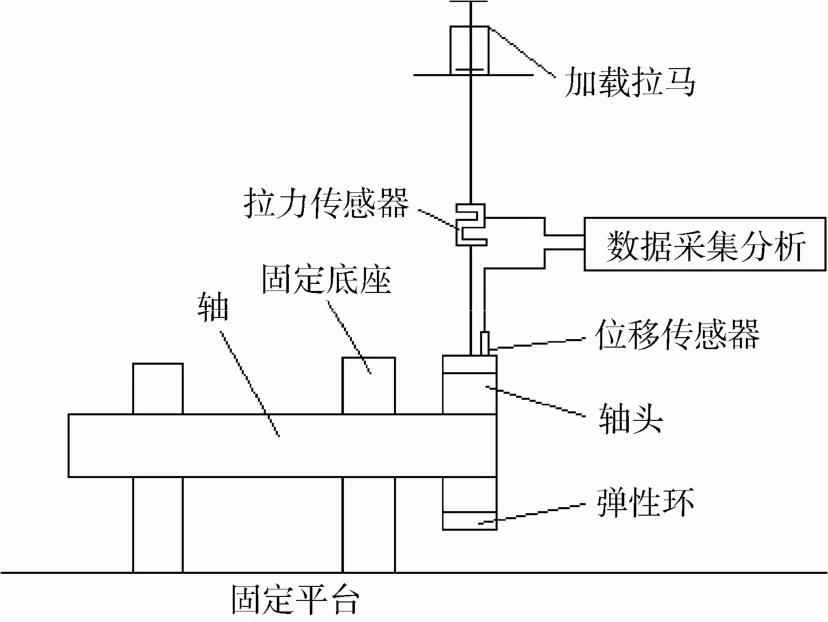
图9　试验台结构示意图Fig. 9　Schematic of structure of test bed

4.2弹性环的几何参数

弹性环的几何参数见表5。

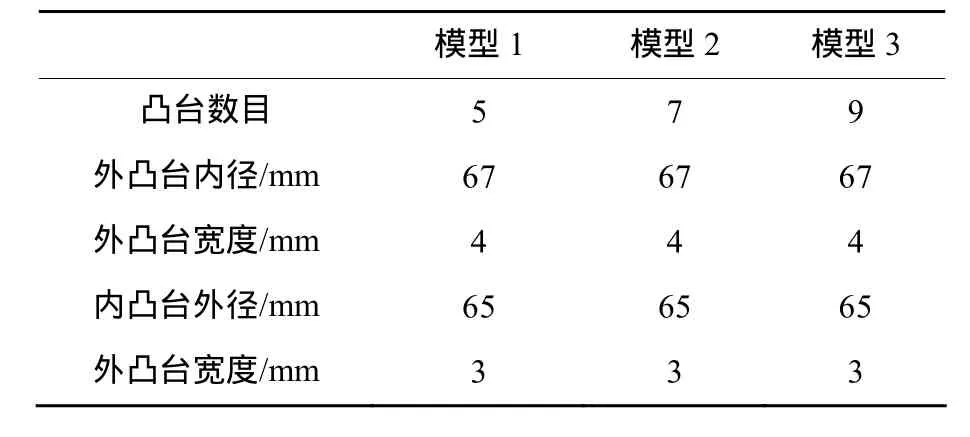
表5　弹性环几何参数Table 5　Geometric parameters of an elastic ring

4.3测试结果

5凸台弹性环加载结果如图10所示。计算得到其刚度见图11。剔除开始加载和卸载区域，取中间加载稳定区域，得到5凸台刚度平均值为0.6×106N/m。

7凸台弹性环加载结果如图12所示。计算得到其刚度见图13。剔除开始加载和卸载区域，取中间加载稳定区域，得到7凸台刚度平均值为1.8×106N/m。

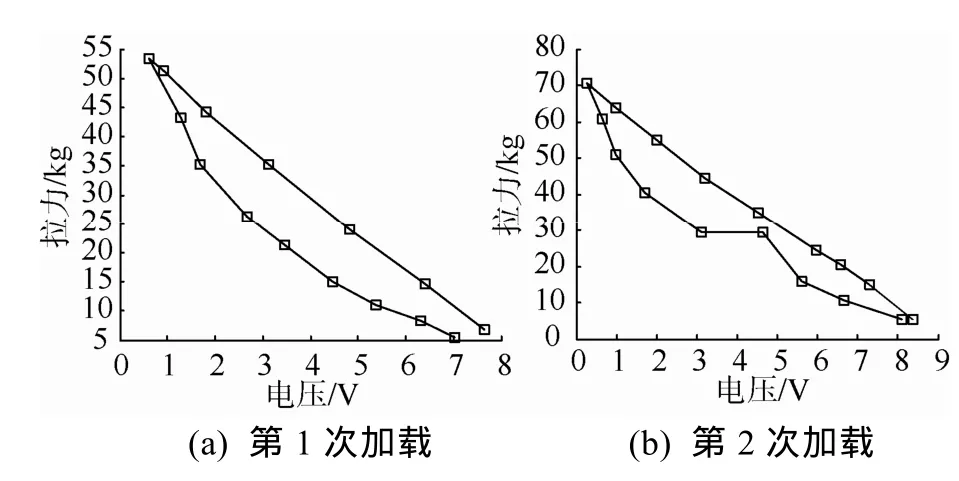
图10　5凸台弹性环加载结果Fig. 10　Loading results of the elastic ring with 5 bosses

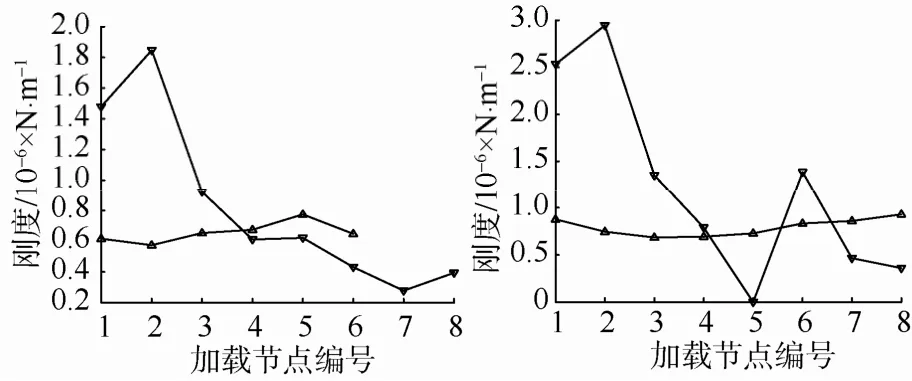
图11　5凸台弹性环静态刚度Fig. 11　Static rigidity of the elastic ring with 5 bosses

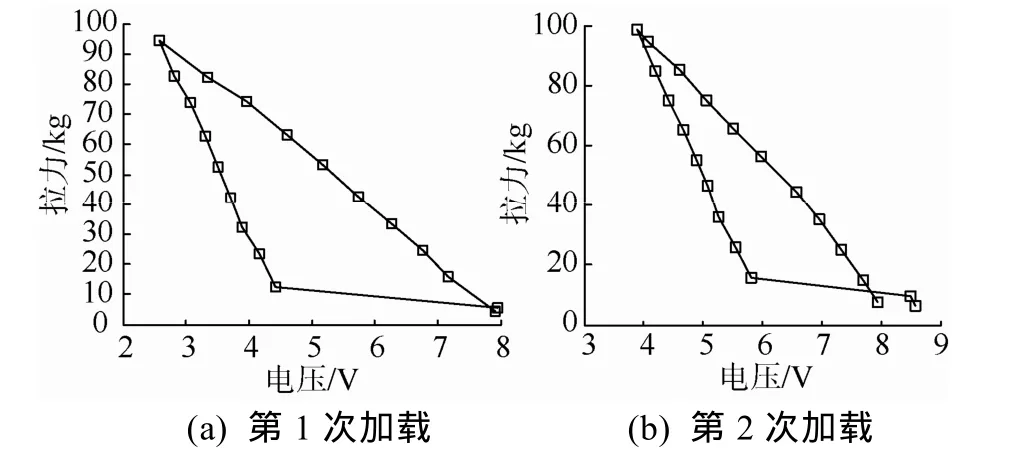
图12　7凸台弹性环加载结果Fig. 12　Loading results of the elastic ring with 7 bosses

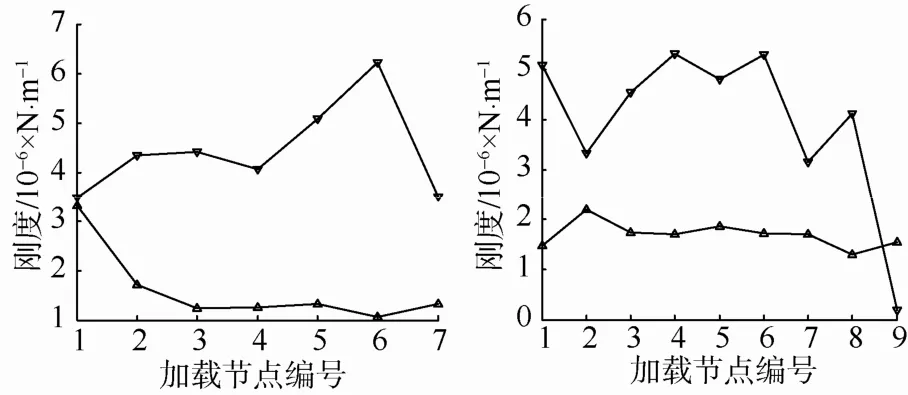
图13　7凸台弹性环静态刚度Fig. 13　Static rigidity of the elastic ring with 7 bosses

9凸台弹性环加载结果如图14所示。计算得到其刚度见图15。剔除开始加载和卸载区域，取中间加载稳定区域，得到9凸台刚度平均值为6 ×106N/m。

不同凸台数目的弹性环刚度计算值及试验值对比见表6。

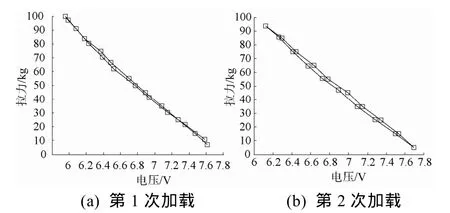
图14　9凸台弹性环加载结果Fig. 14　Loading results of the elastic ring with 9 bosses

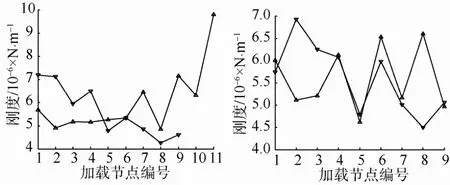
图15　9凸台弹性环静态刚度Fig. 15　Static rigidity of the elastic ring with 9 bosses

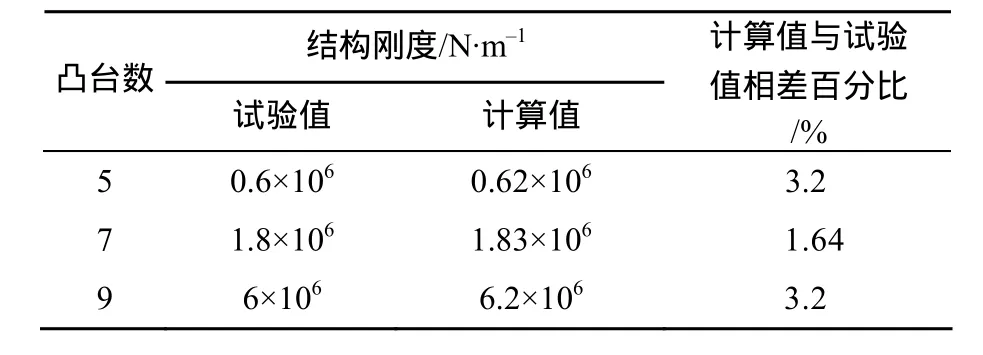
表6　不同凸台数目的弹性环刚度计算值与试验值对比Table 6　Comparison between calculated rigidity and test one of the elastic ring with different boss number

5　结论

本文运用有限元方法计算了弹性环的刚度，并从结构参数和安装尺寸等方面分析了弹性环的刚度特性，得到如下结论。

1）凸台数目的增加，弹性环刚度非线性增大，且增大速度越来越快； 凸台宽度增加时，刚度呈线性增大，增大幅值很小； 凸台高度增加时，刚度呈非线性减小； 环厚度增加时，刚度呈非线性增大。

2）弹性环在一个结构周期内不同位置处的刚度变化不大，因此安装时无需考虑凸台位置；弹性环与刚性环的装配尺寸对弹性环的刚度影响较大，随着过盈量增大，弹性环的径向刚度变大，因此装配时应考虑径向装配尺寸。

［1］顾家柳. 转子动力学［M］. 北京： 国防工业出版社，1985.

［2］龙向阳，洪杰，张大义，等. 弹性环刚度强度的分析方法与力学特性研究［J］. 热能动力工程，2010，25（2）： 145-479.

Long Xiang-yang，Hong Jie，Zhang Da-yi，et al. Study of the Methods for Analyzing the Rigidity and Strength of an Elastic Ring and Its Mechanics Characteristics［J］. Journal of Engineering for Thermal Energy and Power，2010，25（2）： 145- 479.

［3］杨军. 弹性环工艺设计［J］. 燃气涡轮试验与研究，1996，3（6）： 51-54.

［4］古远兴，肖育祥. 弹性环的设计、试验与应用［C］//中国航空学会第八届发动机结构强度振动学术会议论文集，1996.

［5］Leontiev M K. Research of Characteristics of Elastic Ring Mounted in Rotor Bearings of Gas-Turbine Engines［J/OL］. ［2010-09-20］. http：//www.alfatran.com/.

［6］马艳红，陆宏伟，朱海雄，等. 弹性环金属橡胶支撑结构刚度设计与试验验证［J］. 航空学报，2013，34（6）： 1301 -1308.

Ma Yan-hong，Liu Hong-wei，Zhu Hai-xiong，et al. Structure Design and Experiments of Elastic Ring-Metal Rubber Damper［J］. Acta Aeronautica Et Astronautica Sinica，2013，34（6）： 1301-1308.

（责任编辑： 陈曦）

Finite Element Analysis of Rigidity Characteristics of Elastic Ring for Gas Turbine Rotor System

LI Ri-zhao
（The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China）

Elastic support stiffness is vital to adjustment and control of critical speed of gas turbine rotor system. In this study，a rigidity computation model of elastic ring was established with finite element method to analyze the effects of elastic ring′s structural parameters，whirling angle and fit clearance on its rigidity. Tests and measurements verified the feasibility and accuracy of the finite element method for calculating the support rigidity of the elastic ring. The results show that the main parameters in rigidity design of the elastic ring should include the number of bosses，the wall thickness and width，and the fit clearance.

gas turbine； rotor system； elastic ring； rigidity； finite element method

TJ630.32

A

1673-1948（2015）01-0055-06

2014-09-05；

2014-10-19.

李日朝（1970-），男，硕士，高工，研究方向鱼雷热动力技术.