回转体超音速入水冲击数值仿真

孙　凯，党建军，郝维敏，蒋　彬

（西北工业大学 航海学院，陕西 西安，710072）

回转体超音速入水冲击数值仿真

孙凯，党建军，郝维敏，蒋彬

（西北工业大学 航海学院，陕西 西安，710072）

入水冲击问题是现代水中兵器的研究热点之一。采用商用CFD软件，使用流体体积函数（VOF）模型并结合动网格技术，仿真了平头回转体模型在亚音速、跨音速以及超音速状态下的入水过程，得到了模型在不同速度下的入水阻力特性、头部直径、液体可压缩性及空气激波对入水过程的影响。仿真结果表明，入水阻力系数峰值随着速度的增加先降低后平缓，峰值宽度逐渐降低； 增大头部直径，阻力系数峰值增加，峰值宽度增加； 水的压缩性会使阻力系数峰值出现的时间延后，数值降低； 空气激波会使接触水面时刻阻力系数降低。

平头回转体； 入水过程； 流体体积函数（VOF）模型； 阻力系数

0　引言

高速射弹运用超空泡技术使得自身航行阻力减小一个数量级，可用于完成拦截鱼雷、击毁水雷、破除水下障碍和猎杀蛙人等攻击和防御任务。高速射弹的入水过程是从空中弹道转入水下弹道的过度环节，受到巨大的冲击载荷，可能会造成弹道失稳甚至结构失效。因此，入水过程对射弹的整个运动过程非常重要。

国外关于入水理论的相关研究始于20世纪20～30年代。G. V. Logvinovich提出的基于能量守恒的空泡截面扩张过程是最早描述空泡发展过程的理论，并成为后续理论研究的重要参考［1］。国内入水过程的理论和数值研究始于上20世纪90年代。王永虎对雷弹头型与入水冲击阻力特征进行了分析，得到头型长细比对入水冲击的影响［2］；陈宇翔等人使用流体体积函数（volume of fluid，VOF）方法研究水平圆柱砰击入水问题，得到了湍流粘性对圆柱入水的影响［3］； 何春涛等人基于RNS方程和VOF模型对回转体垂直匀速入水进行了数值仿真，得到了空泡形态随时间的变化规律［4］； 邱海强等人使用混合模型对不同头型回转体入水过程进行了数值仿真，得到不同头型对入水冲击载荷和空泡形态的影响［5］。

目前，对于射弹入水问题的研究主要采用试验和数值仿真2种方法。相较试验研究成本高、周期长、结果不精确等缺点，数值仿真方法具有优势。这里采用计算流体力学（computational fluid dynamics，CFD）方法，仿真了平头回转体模型在亚音速、跨音速以及超音速状态下的入水过程，分析了水可压缩性和空气可压缩性对入水冲击的影响。

1　模型建立与验证

1.1数学模型

1）Tait状态方程

当水受到较大的压力时，需要考虑水的压缩性影响，文章应用的水可压缩模型建立在Tait方程基础上。Tait方程在仿真水下爆炸等方面应用广泛。不含温度修正的Tait方程为

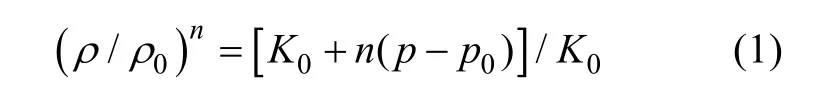
其中： p0是水的参考绝对压力；0ρ是在参考压力下水的参考密度； K0是在参考压力下的参考体积弹性模量； n是密度指数； p是水受到的绝对压力； ρ是在压力为p时的密度。

为了使可压缩流动中的压力计算结果一定，需要在压力修正方程中加入与声速有关的项。利用可压缩流体的声速理论可得简单的声速方程

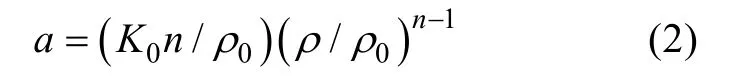
文中研究的工况涉及到跨超声速入水，因此流体的材料属性均使用可压缩流体。

2）6自由度动网格模型

6自由度求解器在计算平移运动时加速度计算较精确，因而文中采用了该求解器模型。在惯性参考坐标系下建立刚体平移运动控制方程为

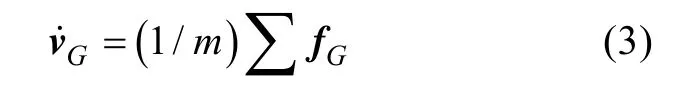
式中： v.G是质心平移加速度矢量； m是刚体质量； fG是作用在物体上的外力。文中回转体运动通过UDF定义6自由度运动网格实现。

1.2计算模型简化及边界条件

建立Φ200 mm×1 000 mm的圆柱形计算域，为减小网格量，加快收敛速度，计算时选取流场的1/2。模型初始位置为水面上一定距离，在空气中飞行一段时间整个流场稳定后再与水面接触。

经典的高速射弹模型大多是长细比很大的回转体，文中仿真的垂直入水工况主要研究的是入水冲击的影响，从节省计算时间成本考虑，计算模型仅保留头部空化器尺寸，后体采用等直径圆柱代替，简化后的计算模型为Φ3 mm×15 mm的平头圆柱，并将其视为刚体。回转体头部阻力系数Cd计算公式为

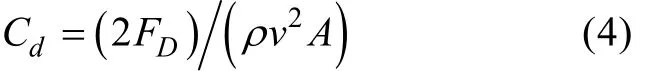
式中：FD为射弹入水过程中收到的阻力，FD= FD（t）； v为运动体入水过程中的瞬时速度，v= v（t）；ρ为水密度；A为运动体特征面积。计算流场为整个流场的1/2，该特征面积取3.532 5×10-6m2。

图1表明了计算域各部分所采用的边界条件：计算域下界采用压力出口，上界采用压力入口；远场以及回转体均为无滑移壁面； 计算域上部为空气域，下部为水域； 回转体运动使用动网格方法实现，靠近回转体及其运动路径附近的区域为运动区域，其余部分为静止区域，两部分采用interface边界条件连接。

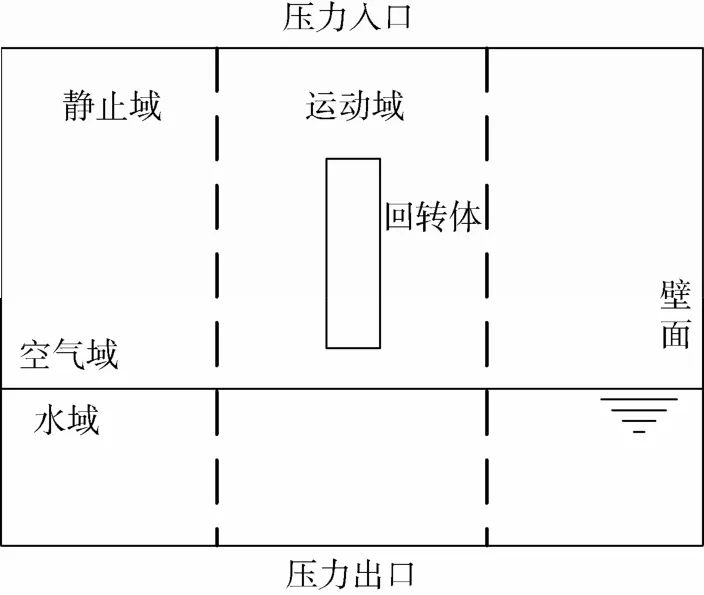
图1　计算流场及边界条件Fig. 1　Calculation of flow field and boundary conditions

Fluent仿真设置： 1）多相流模型选择VOF模型，主相为水，副相为空气和水蒸气； 2）湍流模型选择Realizable k-ε模型； 3）压力速度场耦合方式选用PRESTO！； 4）水使用可压缩流体模型； 5）开启空化模型。

1.3模型验证

为验证上述计算模型的合理性，选取相关论文中的典型试验工况进行数值仿真分析，评估其合理性。M.Schaffar等对圆柱体在1 036 m/s速度下入水进行了试验研究，得到了该试验工况下的流场分布［6］。

图2给出了回转体在入水25 cm深度后的流场分布，可以看出回转体在水中形成了完全包裹自身的超空泡。图3给出了回转体入水后距离头部不同位置处的空泡直径，其中Serebryakov、Levinson是2种数值计算结果，Measurement是试验得到的结果。从图3中可以看出，文中使用的计算模型得到的结果与Serebryakov的数值仿真结果基本一致，与试验的最大误差不超过12.5%。

图2　试验与仿真结果流场对比图Fig. 2　Comparison between experimental and simulated flow field

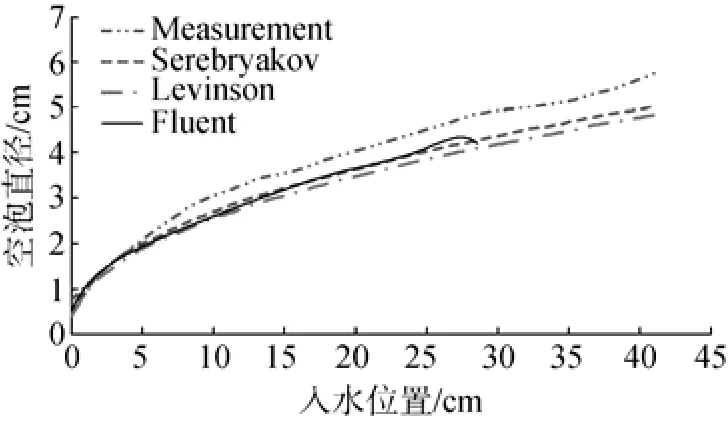
图3　空泡外形对比图Fig. 3　Comparison of cavitation outlines

2　仿真结果与分析

2.1回转体高速入水流场分析

图4和图5显示的是回转体以1 000 m/s工况下不同位置处的水相云图和蒸汽相云图。

从图4可看出，回转体在入水过程中各个阶段的空泡发展过程。回转体从距离水面20 mm处开始下落，接触水面后，水面受到冲击向四周飞溅； 随着回转体继续下落，形成开口空泡并不断发展； 在入水深度达到2倍回转体长度后，空泡上端依然没有闭合趋势。

图4　1 000 m/s速度入水阶段水相体积分数云图

图5　1 000 m/s速度入水阶段蒸汽相体积分数云图Fig. 5　Contour of vapor volume fraction in water entry phase at a speed of 1 000 m/s

从图5可以看出，在空泡内气相和水相的临近区域产生了大量的水蒸气。这是因为回转体入水速度超过声速，空气不能及时补充进空泡内，导致空泡内的压力低于空化压力，产生了空化现象。正是由于空化现象，入水空泡内气相和水相的交界面变得“凹凸不平”。

2.2速度对冲击阻力系数的影响

图6显示的是回转体以1 000 m/s速度入水过程阻力系数在峰值附近的变化过程。在空中飞行阶段，由于空气的阻力很小，阻力系数很小； 回转体接近水面，阻力系数迅速增大，在2×10-5s时回转体与水面接触，此时阻力系数为2.5； 回转体继续运动，阻力系数增大，在2.02×10-5s时阻力系数达到最大值3.23； 阻力系数在达到最大值后逐渐降低，整个冲击峰值持续约0.12×10-5s。

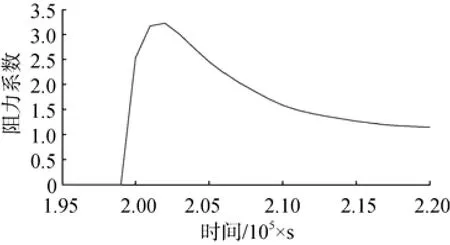
图6　1 000 m/s速度入水阻力系数峰值放大图Fig. 6　Enlarged view of peak value of drag coefficient in water entry phase at a speed of 1 000 m/s

图7 显示的是回转体以不同速度入水时冲击阻力系数峰值及其宽度对比。从图7可以看出，阻力系数峰值随着速度增加呈现先减小后平稳的趋势。在100～300 m/s速度范围内阻力系数峰值随着入水速度的增加而迅速降低； 而在500 m/s及以上速度入水，冲击阻力系数峰值降低得不明显。入水峰值宽度时间处于10-5s量级。峰值宽度随着速度的增大逐渐减小。在1 000 m/s及以上速度，峰值宽度改变很小。

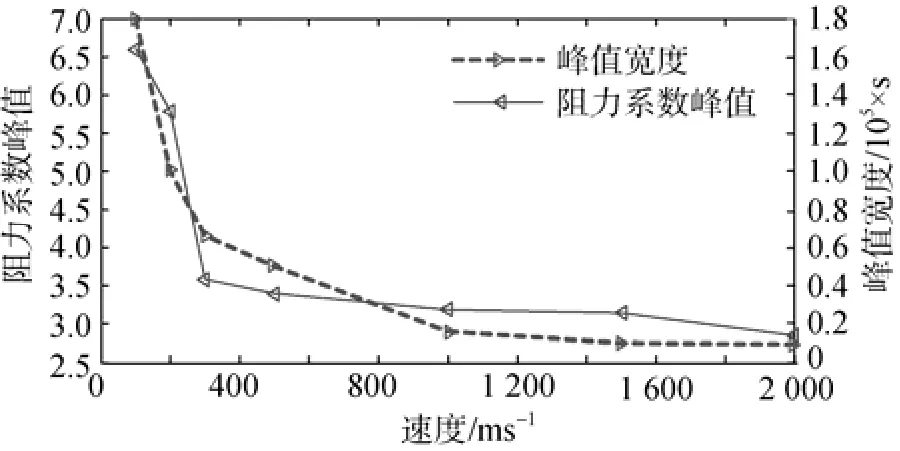
图7　不同速度工况下阻力系数峰值和宽度对比图Fig. 7　Comparison of peak values and peak widths of drag coefficient at different speeds

2.3头部直径对冲击阻力系数的影响

计算选取速度为1 000 m/s工况，原有计算模型头型及长度不变，头部直径分别扩大为原来的2倍和5倍，研究头部直径对阻力系数的影响。

Q 1:燃烧室输出到水浴的热量;Q 2:水浴传递给管程内LNG的热量;C:水的热容;T 1:水浴温度;T 2:管程LNG的温度;R:水浴传热热阻;Gp 1:主被控对象(NG出口温度);Gp 2:副被控对象(水浴温度);Gc1:主回路控制器;Gc2:副回路控制器;τ:副被控对象时滞;τ1:主控对象存在时滞;J(s):燃料气的干扰;E(s):入口LNG的干扰;GE(s):入口LNG的传递函数;Ge(s):前馈补偿通道函数;Y 1(s):主回路的输出;Y 2(s):副回路的输出。

图8显示的是不同头部直径以1 000 m/s速度入水的阻力系数变化。从图中可以看出3种直径的阻力系数依次增大，其值分别为3.38，4.42和5.39，峰值宽度分别为1.6×10-6s，2.9×10-6s和4.5×10-6s。这是因为随着头部直径变大，侧向排开迎流面水的困难增加，阻力系数峰值增加，入水以后阻力系数下降缓慢。

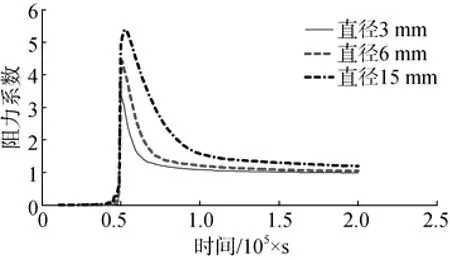
图8　不同头部直径阻力系数对比Fig. 8　Comparison of different drag coefficients for different head diameters

2.4水可压缩性对冲击阻力系数的影响

从理论研究和生活经验都可以知道，在冲击速度达到一定大小后，水不能按照低速下的不可压缩流体对待，需要考虑水的压缩性。

图9显示的是不同速度工况下的水可压缩性对阻力系数的影响。从图中可以看出，在速度为200 m/s时，考虑水可压缩性情况下阻力系数峰值为5.8，不考虑水可压缩性情况下为6.2，两者相对误差为6.9%。同时，由于接触水面时对水有压缩作用，考虑水压缩性情况下入水冲击峰值出现的时间发生后移； 在速度为500 m/s时，考虑水压缩性情况下阻力系数峰值出现的时间同样发生延后，其值为3.2，而在水不可压缩情况下冲击阻力系数为4.4，两者的相对误差达到了37.5%。可见在入水速度为500 m/s时，水的可压缩性对入水冲击阻力影响非常巨大，不能忽略不计。

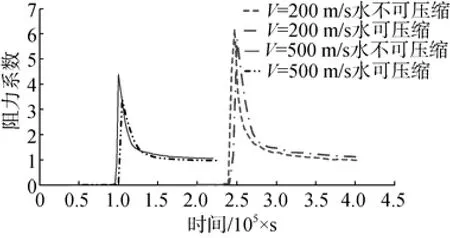
图9　不同速度工况下水可压缩性对比Fig. 9　Comparison of water compressibility at different speeds

2.5空气压缩性对冲击阻力系数的影响

当回转体在空气中以超声速运动时，会压缩空气产生激波。回转体接近水面时，压缩空气与水相互作用是影响冲击力的一个重要因素。计算采用如下策略： 射弹在空气中运动时空气和水同时使用可压缩模型； 当射弹与水面接触阻力系数达到峰值，关闭空气的可压缩性，保留水的可压缩性直到阻力系数趋于某一稳定值，计算结束。

图10显示的是回转体以1 000 m/s速度在空气中飞行的压力云图。从图中可以看出，回转体在空气中飞行，产生了脱体激波。当回转体接近水面时，激波与水面相互作用使临近的水相区域产生了压力梯度。

图11和图12为速度1 000 m/s和2 000 m/s时，考虑与不考虑空气压缩性情况下入水阻力系数峰值的对比。从图中可知，回转体接近水面过程中，考虑空气可压缩情况下的阻力系数开始增大的时间比空气不可压缩要晚，阻力系数峰值出现的时间延后； 速度为1 000 m/s时，在回转体与水接触瞬间，考虑空气可压缩情况的阻力系数为2.55，不考虑空气可压缩情况的阻力系数为3.25，两者相差27.5%。这是因为可压缩空气在回转体接近水面过程中起到了“空气垫”作用，使得阻力系数降低。速度为2 000 m/s时，在回转体与水接触瞬间，考虑和不考虑空气可压缩情况的阻力系数分别为2.2和2.7，两者相差22.7%。

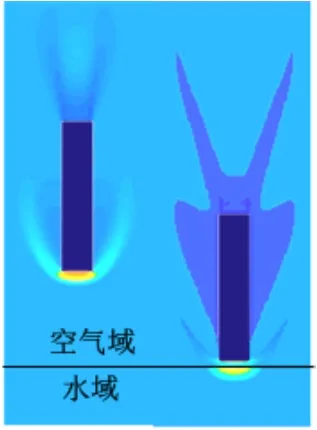
图10　1 000 m/s速度空中飞行压力云图Fig. 10　Pressure contour in air for flight at a speed of 1000 m/s

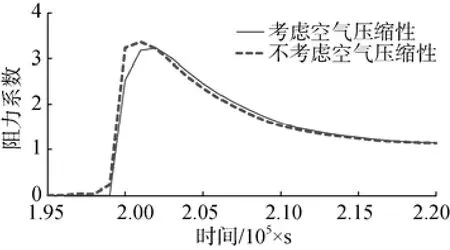
图11　1 000 m/s速度工况空气可压缩性对比Fig. 11　Comparison of air compressibility at a speed of 1 000 m/s

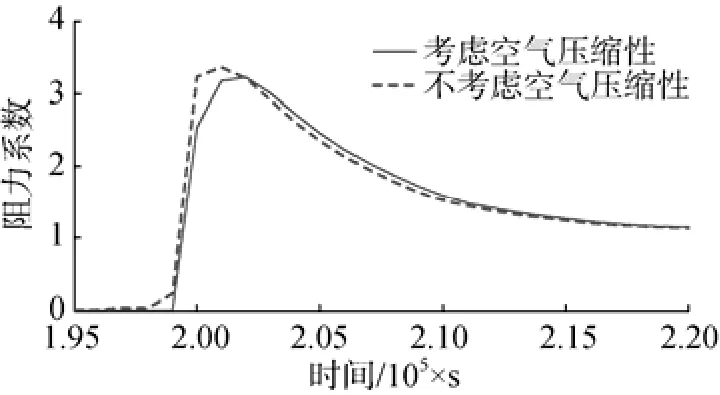
图12　2 000 m/s速度工况空气可压缩性对比Fig. 12　Comparison of air compressibility at a speed of 2 000 m/s

3　结论

采用CFD方法模拟了平头回转体模型在亚音速、跨音速以及超音速状态下的入水过程，分析了水可压缩性和空气可压缩性对入水冲击的影响，得到了如下结论。

1）平头回转体以1 000 m/s速度入水，在入水深度达到2倍体长时，入水空泡依然没有闭合的趋势，且在气液两相的交界区域附近产生了大量水蒸气；

2）平头回转体入水速度在100～2 000 m/s范围内，入水冲击阻力系数峰值先减小后平稳。峰值宽度处于10-5s量级，其大小随着速度的增大呈现逐渐减小趋势； 在1 000 m/s速度工况下，增加头部直径，阻力系数峰值增加，峰值宽度增加；

3）考虑水压缩性的影响，模型入水冲击阻力系数峰值减小，峰值的时间延后。在速度为200 m/s时，考虑水可压缩性和不考虑水可压缩情况下，阻力系数相对误差为6.9%； 在速度为500 m/s时，两者的相对误差达到了37.5%；

4）考虑空气可压缩性，模型接近水面时，激波与水面相互作用使临近的水相区域产生压力梯度。模型在空气中运动的阻力系数增大的时间延后； 在接触水面时刻的阻力系数减小； 阻力系数出现峰值的时刻延后。

［1］Logvinovich G V. Hydrodynamics of Free-boundary Flows［J］. Jerusalem，Israel Program for Scientific Translation，1972： 103-113.

［2］王永虎. 空投雷弹入水冲击头型特性参数分析［J］. 航空计算技术，2010，40（11）： 14-17.

Wang Yong-hu. Nose Performance Description Coefficience of Airborne Torpedo and Deep-mine during Water-entry Impact［J］. Aeronautical Computing Techbique，2010，40（11）： 14-17.

［3］陈宇翔，郜冶，刘乾坤. 应用VOF方法的水平圆柱入水数值模拟［J］. 哈尔滨工程大学学报，2011，32（11）： 1439-1442.

Chen Yu-xiang，Gao Ye，Liu Qian-kun. Numerical Simulation of Water-entry in a Horizontal Circular Cylinder Using the Volume of Fluid（VOF）Method［J］. Journal of Harbin Engineering University，2011，32（11）： 1439-1442.

［4］何春涛，王聪，闵景新，等. 回转体匀速垂直入水早期空泡数值模拟研究［J］. 工程力学，2012，29（4）： 237-243.

He Chun-tao，Wang Cong，Min Jing-xin，et al. Numerical Simulation of Early Air-Cabity of Cylinder Cone With Vertial Water-entry［J］. Engineering Mechanics，2012，29（4）： 237-243.

［5］邱海强，袁绪龙，王亚东，等. 回转体高速垂直入水冲击载荷和空泡形态仿真［J］. 鱼雷技术，2013，21（3）： 161-164.

Qiu Hai-qiang，Yuan Xu-long，Wang Ya-dong，et al. Simulation on Impact Load and Cavity Shape in High Speed Vertical Water Entry for an Axisymmetric Body［J］. Torpedo Technology，2013，21（3）： 161-164.

［6］Schaffar M，Rey C，Boeglen G. Behavior of Supercavitating Projectiles Fired Horizontally in a Water Tank： Theory and Experiments［C］//The 35th AIAA Fluid Dynamics Conference and Exhibit，Toronto，Ontario Canada，2005.

（责任编辑： 陈曦）

Numerical Simulation on Vertical Water Entry Impact of Axisymmetric Body at Supersonic Speed

SUN Kai，DANG Jian-jun，HAO Wei-min，JIANG Bin
（School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

Water entry impact is one of the hot topics in the modern underwater weapons research. With the volume of fluid （VOF）model and dynamic mesh in commercial CFD software，the water entry processes of an axisymmetric body with flat top are simulated at subsonic，transonic and supersonic speeds，respectively. The drag coefficient，head diameter，water compressibility and the effect of air shock wave on the water entry processes of the simulated model are acquired at three different speeds. Simulation results show that： 1）with the increase of speed，the peak value of drag coefficient first decreases then remains stable in the end，and the width of peak value decreases gradually； 2）the peak value and its width of drag coefficient increases with the increase in head diameter； 3）the water compressibility delays the appearance of the peak value of drag coefficient and reduces the peak value； and 4）air shock wave reduces the value of drag coefficient at water surface.

axisymmetric body； water entry process； volume of fluid（VOF）model； drag coefficient

TJ630.1

A

1673-1948（2015）01-0002-05

2014-11-17；

2014-12-08.

孙凯（1989-），男，在读硕士，主要研究方向为水下航行器设计.