文丘里型导管对潮流涡轮机作用荷载和转速的影响
董 雪,王 立
(中国电建集团华东勘测设计研究院有限公司,浙江 杭州 311122)
我国沿海地区人口密集,经济发达,沿海11个省(自治区、直辖市)人口占全国的40%,工农业总产值占全国的70%,但能源问题制约着沿海地区的经济发展。沿海地区拥有丰富的海洋能(潮汐能、潮流能、波浪能、温差能和盐差能等)资源,是一种可再生绿色能源。因此,加快海洋能的开发利用对沿海地区乃至全国的经济与社会发展和国防建设都具有十分重要的意义。目前,潮流能发电涡轮机可分为水平轴和垂直轴两种。水平轴涡轮机的旋转轴与来流方向平行,其发电功率大小受来流方向影响较大。垂直轴涡轮机的旋转轴与来流方向垂直,叶片获得的能量大小不受水流方向的影响。最初的潮流能发电借鉴了风力发电和船舶螺旋桨等技术,涡轮机水动力特性的预测、潮流发电的设计和机械结构的优化,大多在这个基础上通过模型试验和数值模拟来研究。但潮流能发电涡轮机在实际运行中会遇到风力发电中不会有的问题,如涡轮机转速较快时会发生空化空蚀现象,影响涡轮机的使用寿命。国外对潮流能发电的研究主要集中在自由流情形,较早的如意大利阿基米德公司(Ponte di Archimede)于2001年研制成一种垂直轴自由流潮流涡轮机,即Kobold潮流能利用装置,这种装置的优点是可适应不同来流方向,但涡轮机扫掠面积较小致使转换效率比较低;英国MCT(Marine Current Turbines)公司于2003年研制出一种水平轴双叶片自由流潮流涡轮机,其后,美国Verdant电力公司、挪威Hammerfest Strom公司等相继研制出水平轴三叶片自由流潮流涡轮机,这种类型的涡轮机结构类似于风力发电涡轮机,主要适用于潮流比较强的海域。Bahaj等[1]指出目前大多数潮流能水平轴涡轮机的设计是基于风能涡轮机的原理,但与风能涡轮机显著不同的是潮流能涡轮机存在自由表面效应和空化空蚀现象。Batten等[2]介绍了潮流涡轮机水动力设计的方法,对涡轮机的空化特性进行了试验研究,并基于叶素理论对潮流涡轮机的水动力特性进行了预测[3]。Bahaj等[4]在拖曳水池中量测了潮流涡轮机的功率和推力。Clarke等[5]基于修正的叶素理论,对反向旋转潮流涡轮机的特性进行了预测。Myers等[6]在循环水洞中测试了水平轴涡轮机不同流速、不同叶片间距、不同转子偏航角工况下的输出功率。Khan 等[7]介绍了可用于河流和潮流的水能转换系统,并对水平轴和垂直轴涡轮机作了分类和定量比较。Jo等[8]指出韩国西海岸和南海岸地区潮流最大速度可达6.5m/s,非常适宜于潮流能的开发利用。Goundar等[9]论述了在太平洋岛屿国家开发利用潮流能资源的必要性,并设计了一种三叶片水平轴潮流发电涡轮机。Kang等[10]利用大涡模拟方法数值模拟了美国Verdant电力公司为纽约东河设计的第4代自由流水平轴涡轮机的水动力特性。
近年来,国内也加大了潮流能利用研究的力度。张亮等[11]介绍了垂直轴涡轮机国内外利用现状和研究进展,提出了需要解决和突破的技术难点。盛其虎等[12]基于叶素理论,采用CFD软件对设计的水平轴涡轮机的水动力特性进行了数值模拟,分析了不同叶梢速度比下的功率特性。林勇刚等[13]针对水下风车与现代风力机结构形式相似而所利用的能量介质不同的特点,利用计算流体力学方法设计了水下风车发电机组的桨叶。王俭超等[14]基于美国NACA(National Advisory Committee for Aeronautics)系列翼型设计了两种模型叶片,利用Fluent软件分析了多种翼型的水动力特性。张雪明等[15]设计了一种双向流自变距水平轴涡轮机,该涡轮机具有自动变距功能以适应双向潮流能。曹高辉等[16]从叶素理论和纳维-斯托克斯方程(N-S方程)出发,计算分析了微型水轮机叶片数、桨距角、尖速比和流速对水动力特性和水轮机功率的影响。付士凤等[17]基于滑移网格技术,采用Fluent软件对垂直轴直叶H型潮流水轮机进行了三维数值模拟,分析了叶片数对水轮机水动力性能的影响。通常,潮流流动缓慢,输入涡轮机的动能较低;此外,潮流方向与水平轴涡轮机的方向未必平行,这样也会损失涡轮机的输入动能。Betz[18]曾提出,流体的动能被转换成机械能的最大效率为59.3%(16/27),即著名的贝茨(Betz)极限。对如何提高涡轮机输入动能这一问题,目前国内外研究较少。英国Rotech公司、德国Schiller公司提出了概念性潮流涡轮机文丘里型导流罩,但没有报道导流罩长径比、面积比对涡轮机转速和作用荷载的影响。本文基于自主研发的水平轴涡轮机及其文丘里型导管,通过理论分析和水槽试验,研究了文丘里型导管对涡轮机的增速作用和对作用于涡轮机上荷载的影响。
1 试验设备与量测技术
试验在大型玻璃水槽中进行。试验装置主要由涡轮机(3D打印机制作)和文丘里型导管(采用不锈钢板由数控机床精加工制成)组成,如图1所示。水流速度由SonTek声学多普勒测速仪(acoustic Doppler velocimeter,ADV)量测,涡轮机转速用Photron Fast Cam APX-RS高速摄影机在HMI-DCI1000W无频闪光源下观测记录。文丘里型导管的收缩段和扩散段采用相同规格,呈对称布置。喉部为有机玻璃,以便观测涡轮机的转速。图2为文丘里型导管与潮流涡轮机示意图(图中D、d分别为文丘里型导管收缩段的进、出口直径;L为收缩段长度;v为来流速度)。

图1 潮流能试验装置
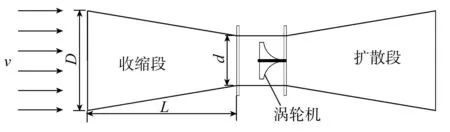
图2 文丘里型导管与潮流涡轮机示意图
在潮流能利用中,涡轮机叶片的设计至关重要。传统的涡轮机叶片采用等弦长、等厚度的二维翼型,这种二维叶片的自重大,潮流推动叶片转动消耗的能量大,导致涡轮机潮流动能转换为机械能的效率低,且需要较高流速的潮流才能使涡轮机获得期望的转速。鉴于此,本文以NACA翼型剖面为基础,设计了如图3(a)所示的潮流涡轮机叶片。此种涡轮机叶片从翼根至翼梢的弦长逐渐变短,厚度逐渐变薄,缩小了叶片的体积,减轻了叶片自重,提高了涡轮机将潮流动能转变为机械能的效率,即使潮流速度很低,涡轮机仍能获得较高的转速(111~865r/min),并且不会发生空化空蚀(图3(b)为涡轮机空化空蚀试验装置)。水槽试验流速v=0.16~0.98m/s,文丘里型导管的长径比L/d=0.5、1.0、1.5,2.0、2.5,其面积比A1/A2=1.00、1.89、3.06、4.52、6.25、8.27(A1、A2分别为收缩段进、出口面积)。

图3 新型潮流涡轮机叶片及其空化空蚀试验装置
2 涡轮机作用荷载和转速的理论分析
2.1 涡轮机作用荷载
潮流对涡轮机的作用荷载主要包括推力、转矩和径向力。推力T可表示为
(1)
式中:A为涡轮机扫掠面积;α为偏流角(涡轮机轴向与来流方向的夹角);CT为推力系数,是偏流角的函数,对于自由流情形,推力系数随偏流角的增大而减小[4],即CT=f(α)=0.85~0.80;ρ为水流密度。对于文丘里型导管,可通过连续性方程将来流速度转换成涡轮机处的流速。
涡轮机的转矩M可表示为
(2)
其中
Q=vAcosαvt=ωr
式中:Q为流量;r为叶片有效半径;vt为切向速度;n为涡轮机转速;ω为旋转角速度,可表示为
ω=2πn/60
(3)
根据牛顿第二定律,径向力F可表示为
(4)
其中
式中:a为向心加速度;m为质量,单位时间的质量为ρQ。
2.2 潮流速度与涡轮机转速的关系
自由流中涡轮机的水平轴向出力P为
(5)
由式(5)可知,涡轮机出力与来流速度的立方成正比。
自由流情形来流功率N1可表示为
N1=FLvcosα
(6)
式中FL为升力,可写成:
(7)
式中CL叶片升力系数。将式(7)代入式(6)得:
(8)
涡轮机旋转产生的功率N2可表示为
N2=Mω
(9)
若不计涡轮机的机械损失,来流功率应等于涡轮机产生的功率:
N1=N2
(10)
将式(8)、式(9)代入式(10)得:
(11)
将式(2)、式(3)代入式(11),得到涡轮机转速计算公式:
(12)
由式(12)可知,自由流情形涡轮机转速n为来流速度v、叶片有效半径r、叶片升力系数CL的函数,其中叶片有效半径r=60mm,作为一阶近似,涡轮机叶片升力系数CL=1.0。当所选叶片的规格及参数确定后,在不考虑机械损失的情况下,涡轮机转速主要取决于来流速度,且呈线性增长。涡轮机转速理论值(式(12)计算值)与本文实测值的比较如图4所示,可见理论值与实测值吻合良好。
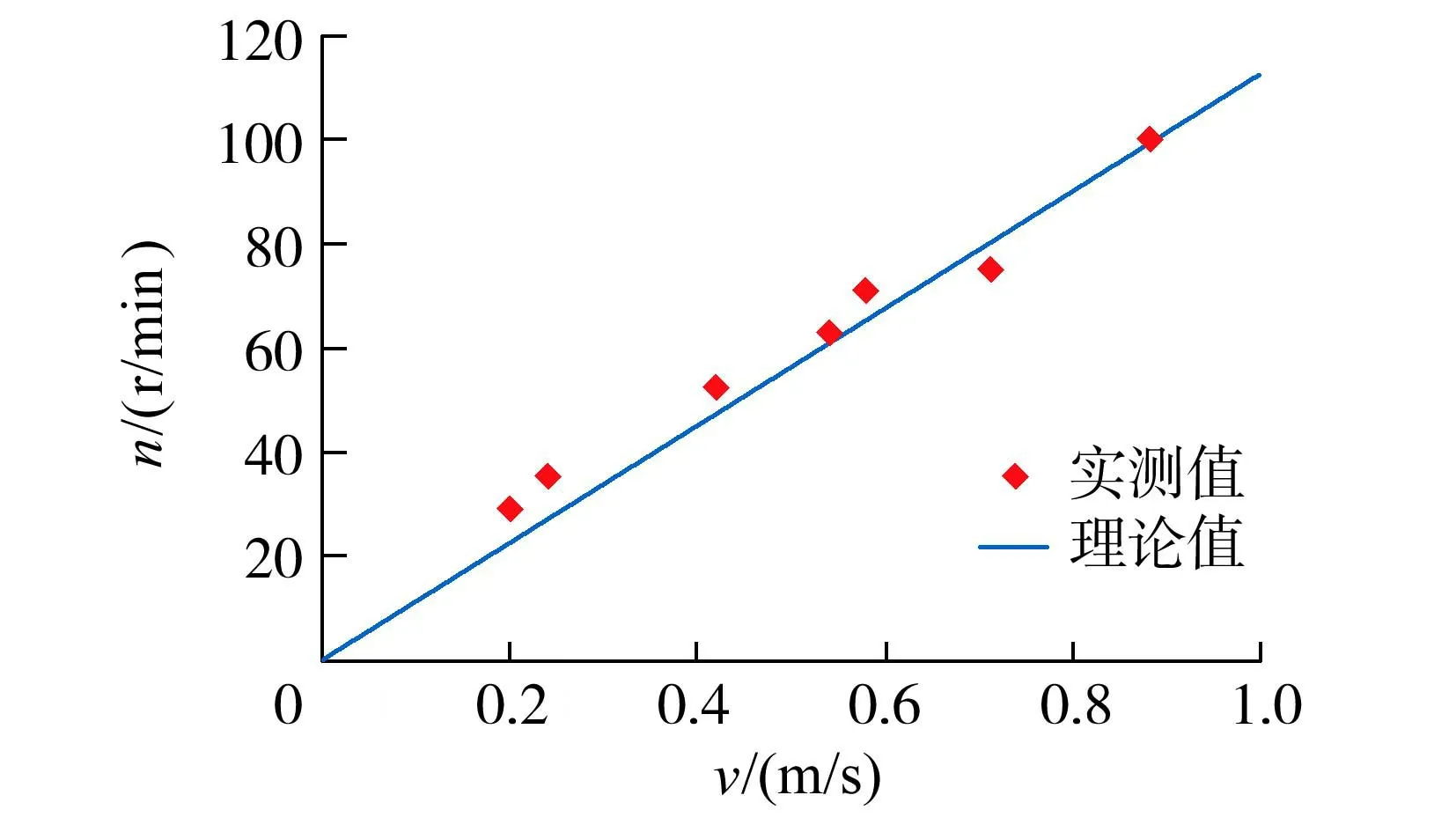
图4 涡轮机转速与来流速度的关系
3 试验结果与分析
3.1 导管长径比对涡轮机作用荷载的影响
本文试验研究了收缩段与扩散段规格相同的文丘里型导管长径比L/d在不同来流速度(v=0.16~0.98m/s)、不同偏流角(α=0°、10°、20°、30°、40°、50°)情形下对涡轮机作用荷载的影响。当导管面积比一定,即A1/A2=(D/d)2=4.00时,改变导管长度L,使L/d=0.5、1.0、1.5、2.0、2.5,将实测流速分别代入式(1)、式(2)和式(4)可得导管不同长径比时作用于涡轮机上的推力、转矩和径向力。以来流速度v=0.54m/s为例,不同长径比情形下水流作用于涡轮机上的推力、转矩和径向力试验结果见表1~3。由表1~3可见,当长径比不变时,推力随偏流角的增大而减小,但对于同一偏流角,推力则不随长径比变化;当长径比不变时,作用于涡轮机上的转矩先随偏流角的增大而逐渐增大,然后随偏流角的进一步增大则逐渐减小,也就是说,转矩随偏流角的变化存在一个极大值,位于偏流角α=30°左右。另外,当偏流角不变时,转矩随长径比的增大而逐渐增大,在L/d=1.5~2.0时达到极大值,然后随长径比的进一步增大而减小;若长径比保持不变,作用于涡轮机上的径向力随偏流角先增大后减小,在偏流角α=30°左右达到极大值。若锁定偏流角,则径向力在L/d=1.5~2.0时达到极大值。
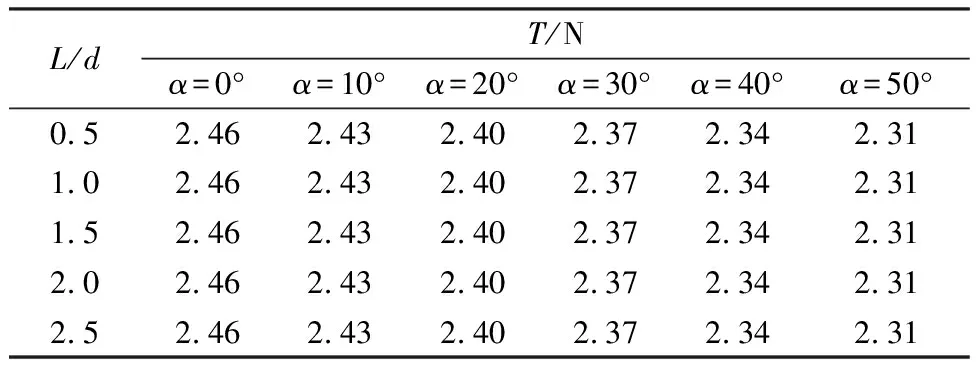
表1 不同导管长径比和偏流角时作用于涡轮机上的推力

表2 不同导管长径比和偏流角时作用于涡轮机上的转矩
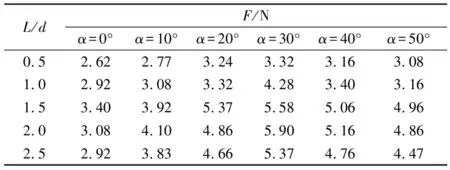
表3 不同导管长径比和偏流角时作用于涡轮机上的径向力
3.2 导管面积比对涡轮机作用荷载的影响
除了导管长径比外,本文还试验研究了文丘里型导管面积比在不同来流速度、不同偏流角情形下对涡轮机作用荷载的影响。当导管长径比一定,即长径比L/d=2.0时,改变导管面积比,使A1/A2=1.89、3.06、4.52、6.25、8.27,将实测流速分别代入式(1)、式(2)和式(4)可得到不同导管面积比情形下作用于涡轮机上的推力、转矩和径向力。仍以来流速度v=0.54m/s为例,不同导管面积比情形下作用于涡轮机上的推力、转矩和径向力见表4~6。从表4~6中不难看出,作用于涡轮机上的推力随导管面积比的增大而增大,并且导管面积比一定时推力随偏流角的增大而减小;作用于涡轮机上的转矩随导管面积比和偏流角的增大而增大,在偏流角α=30°左右存在极大值;作用于涡轮机上的径向力表现出与转矩同样的变化规律。
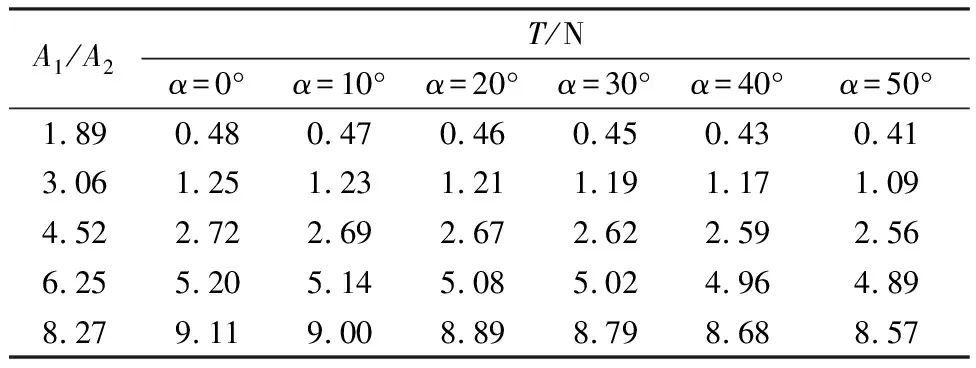
表4 不同导管面积比和偏流角时作用于涡轮机上的推力
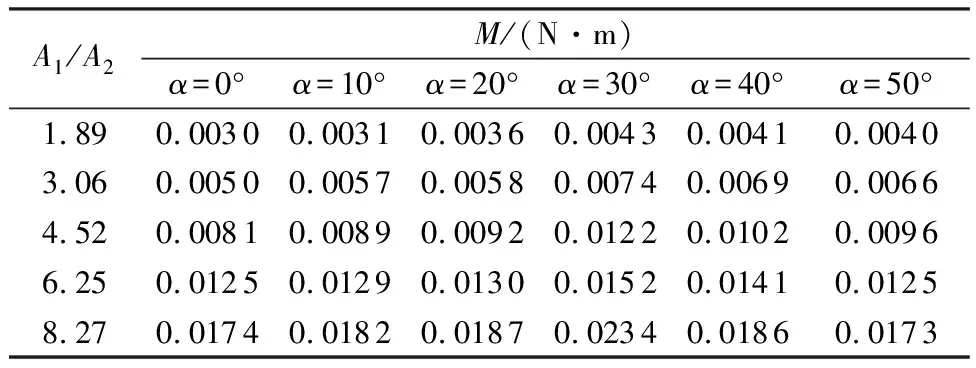
表5 不同导管面积比和偏流角时作用于涡轮机上的转矩

表6 不同导管面积比和偏流角时作用于涡轮机上的径向力
3.3 导管长径比对涡轮机转速的影响
以来流速度v=0.54m/s为例,不同来流偏流角情形下涡轮机转速随文丘里型导管长径比的变化如图5所示(图中L/d=0.0对应于自由流情形,即没有文丘里型导管)。由图5可见,涡轮机转速起初随导管长径比的增大而增大,在不同偏流角时,均在L/d=1.5~2.0处达到极大值,然后随长径比的进一步增大而减小。相对于自由流情形,文丘里型导管的存在可以显著提高涡轮机的转速。由于潮流比较缓慢,输入自由流涡轮机的功率较低,利用文丘里型导管可大幅度提高输入涡轮机的功率,从而提高潮流能发电涡轮机的出力。但文丘里型导管既不能太长,也不能太短,以L/d=1.5~2.0为宜。从图5还可以看出,涡轮机的转速不仅与导管长径比有关,而且还取决于偏流角。涡轮机转速随偏流角的增大而逐渐升高,当α=30°时转速升至最高,随后随着偏流角的进一步增大而逐渐降低,这与涡轮机叶片的攻角有关。
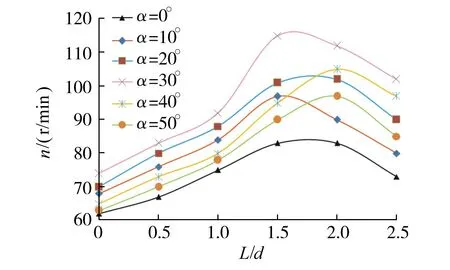
图5 涡轮机转速随导管长径比的变化曲线
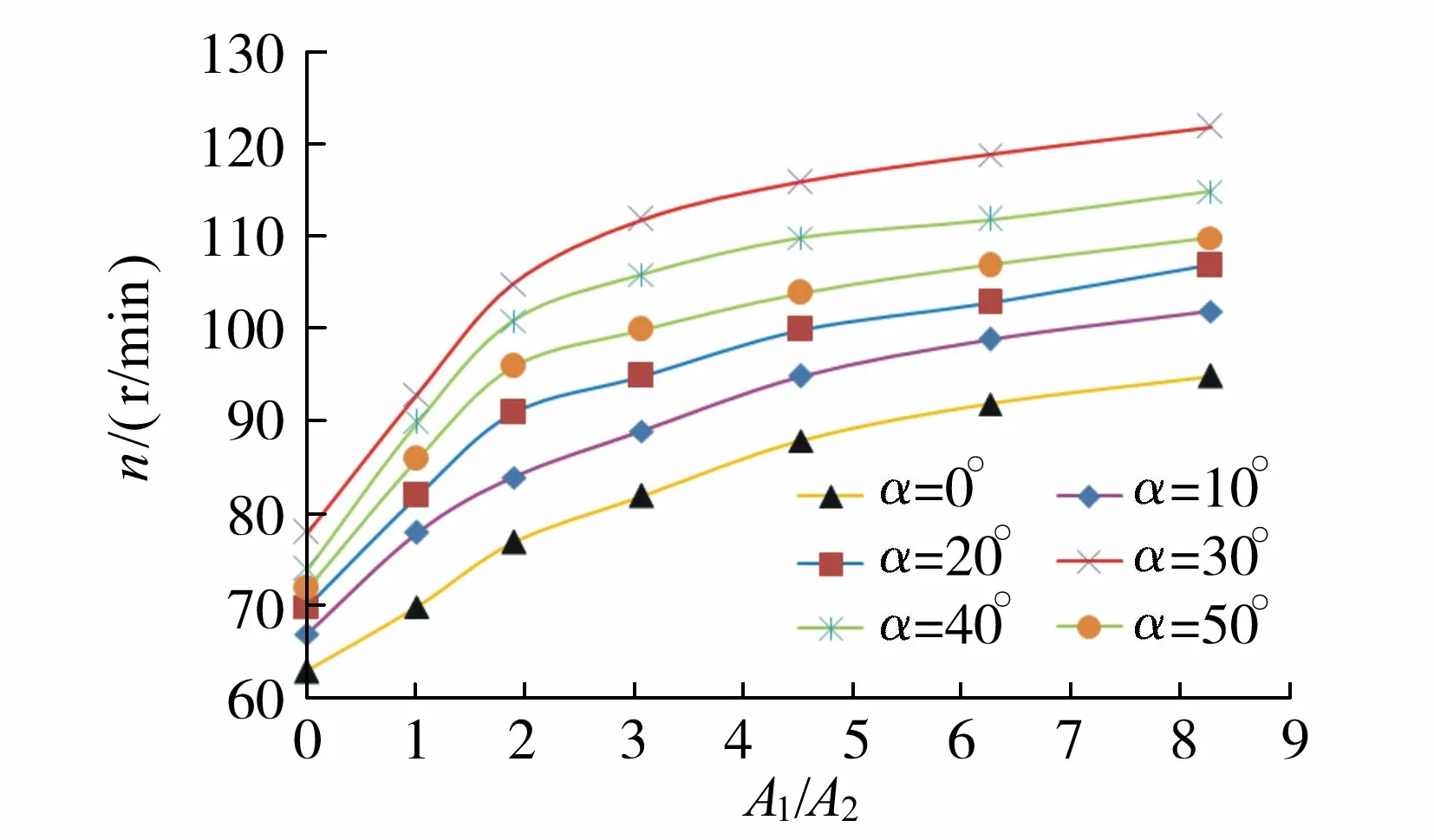
图6 涡轮机转速随导管面积比的变化曲线
3.4 导管面积比对涡轮机转速的影响
为便于比较,仍以来流速度v=0.54m/s为例,图6为文丘里型导管在不同偏流角时涡轮机转速随面积比的变化关系(图中A1/A2=0为自由流情形,A1/A2=1为等直径管)。从图6不难看出,文丘里型导管面积比的增大可明显提高涡轮机的转速,当A1/A2=8.27时可使涡轮机转速提高超过50%。显然,利用文丘里型导管可显著提高潮流能的出力。当A1/A2<2时,涡轮机转速随导管面积比增大急剧升高,而当A1/A2>2时,涡轮机转速随导管面积比的逐渐增大而缓慢增大。这意味着,尽管并非文丘里型导管越长涡轮机转速越高,但其面积比增大却使涡轮机转速逐渐升高。从图6还可以看出,涡轮机转速随来流偏流角的变化存在临界偏流角,若α<30°,涡轮机转速随偏流角的增大而升高;相反,若α>30°,涡轮机转速则随偏流角的增大而降低。
4 结 论
a.基于自主研发的文丘里型导管潮流涡轮机,从理论上推导出潮流作用于涡轮机上荷载的计算公式,可供初步设计时估算潮流作用于涡轮机上的推力、转矩和径向力。
b.当导管长径比不变时,推力随偏流角的增大而减小,转矩和径向力随偏流角的变化于偏流角α=30°时存在极大值;当偏流角不变时,转矩和径向力随长径比的变化在L/d=1.5~2.0时达到极大值;推力、转矩和径向力随导管面积比的增大而增大,但面积比一定时,随偏流角的增大存在极大值。
c.文丘里型导管可显著提高涡轮机的转速,其大小取决于导管的长径比和面积比;在不同偏流角情形下,转速在长径比L/d=1.5~2.0时最大,这意味着导管不宜太长或太短;转速随导管面积比的增大而增大。
d.与自由流情形相比,文丘里型导管不仅可以增大潮流速度,同时还具有矫正偏流的作用,从而提高输入涡轮机的动能。

