钢管混凝土系杆拱桥吊杆施工张拉力计算的研究

刘波

【摘要】吊杆张拉是在梁拱组合体系桥的施工过程中体系转换的关键工序。可是吊杆先后顺序的张拉必然会相互之间产生影响。为了减少后期对索力进行调整的工作，我们使用迭代计算的方法，尽量在吊杆的张拉过程中一次达到吊杆张拉控制力，本文以一座梁拱组合体系桥为例，运用该算法，计算出张拉力的理论值，显示了该方法能取得较好的效果。

【关键字】系杆拱桥；吊杆施工张拉力；迭代法

1、前言

梁拱组合结构的设计特点是，外部为静定结构，内部为高次超静定结构，拱肋是其主要的承重构件，此外还包括加劲纵梁，以及它和横梁组成的平面框架，拱肋和平面框架结构通过吊杆的联系来共同受力。该类型的桥常用跨径为40m-120m。梁拱组合式桥梁主要形式包括：简支梁拱组合式、单悬臂梁拱组合式以及连续梁拱组合式三个大类。连续梁拱组合式桥的跨越能力为最大，且形式多种多样。

在施工过程中，进行结构体系转换的关键步骤就是进行吊杆的张拉。对于整个桥梁来说，吊杆力是非常重要的。但由于张拉顺序的影响，后张拉的吊杆会影响先张拉的吊桿，使得最终的张拉力与张拉控制力不符，要达到张拉控制力的值使得我们必须进行调索工作，为了避免后期的调索工作，我们通过一次张拉达到张拉控制力。

本文通过理论分析并结合实例，验证了吊杆施工张拉力一种可行的迭代计算方法。

2、工程概况

某桥梁全长68米，桥型为简支梁拱组合体系桥。桥面宽度为26米，机动车道使用双面坡，坡向桥梁的两侧，坡度为2%，人行道坡为向道路中心线，坡度是1.5%。上部结构使用的是刚性拱，柔性吊杆。该桥计算跨径为67.6m，采用二次抛物线为拱轴线，矢高为16.9m，矢跨比为1/4。拱肋采用的是圆端型钢管混凝土拱，钢管拱肋的宽度为160cm，高度为140cm，钢管以及腹板壁的厚度为1.8cm，内部填充的是C50微膨胀混凝土。主梁采用的是箱型断面，吊杆处高度为188cm，底宽为300cm，腹壁厚100cm。吊杆的间距为4.6m，拱肋设置吊杆一共13根。吊杆采用的是127?7镀锌的高强钢丝索，吊杆位于桥面以上2m部分外包不锈钢套管。桥面的2%横坡由横梁的高度变化来进行调整；桥面板采用的是整体式实心板，厚度为25cm。拱肋横向联系采用由钢管焊接而成的桁架风撑，。主梁和横梁是预应力混凝土结构。桥台采用实体式结构，桥台基础为直径1.2米钻孔灌注桩，桩端持力层为中风化灰岩，入岩深度应不小于1米。

3、迭代法计算吊杆施工张拉力

3.1 迭代法计算原理

吊杆施工张拉力的计算方法有很多种，在此我们采用迭代法。迭代法简单直观，既可用于简单结构，也适用于大跨度桥梁的几何非线性计算，并且容易借助计算机采用有限元软件来实现。迭代法对于不复杂结构的收敛速度较快。

正装法的基本思路是：采用正序分析实际结构的施工过程，就是按照施工方案，依次施工相应的结构，同时添加上相应的荷载，以模拟施工过程中，结构受到荷载时一系列的应力状态。由于钢管混凝土系杆拱桥是多次超静定结构，采用正装算法一般需要进行多次迭代来求出索力，故应用正装法来计算索力地基本思路为： 以张拉结束后各吊杆的张拉控制力值为目标值，进行一轮正装计算，得到一个张拉完成时的索力值，将该索力值与目标索力值进行比较，求出两次差值，得到新一轮的安装索力，再进行新一轮的计算，直至逼近目标值为止。

以吊杆张拉控制力为初始值，进行模型分析计算，得到一个张拉完成的值，以初始值和完成后的值的差值为修正量，进行多次迭代计算，最终得到实际张拉值。为了使最终计算结果准确，可以将差值的值取的足够的小，这样得到的计算结果就能保证吊杆张拉完成的索力值与设计张拉力值基本一致。

3.2 吊杆的施工张拉力计算

以该钢管混凝土系杆拱桥为例，使用Midas Civil对结构进行有限元分析。采用上述的计算方法来计算吊杆施工张拉力。

该桥采用的是先梁后拱的施工方法，具体施工步骤如下：搭设施工用满堂支架→支架上现浇主梁以及拱肋钢管预埋段→第一批次纵向预应力钢束以及横向预应力束张拉→拱肋、横撑的吊装施工→第二批次纵向预应力束张拉→灌注钢管内的混凝土→张拉吊杆（分两批次张拉到位）→张拉剩余的主梁预应力筋→拆除支架→施工桥面铺装。

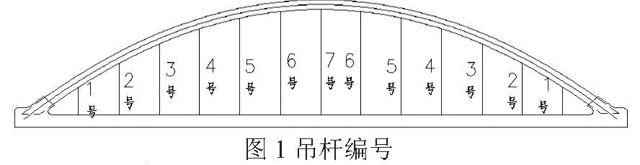
吊杆的张拉顺序：4#→5#→6#→7#→3#→2#→1#，前后两次张拉吊杆顺序相同，吊杆编号如图1所示。

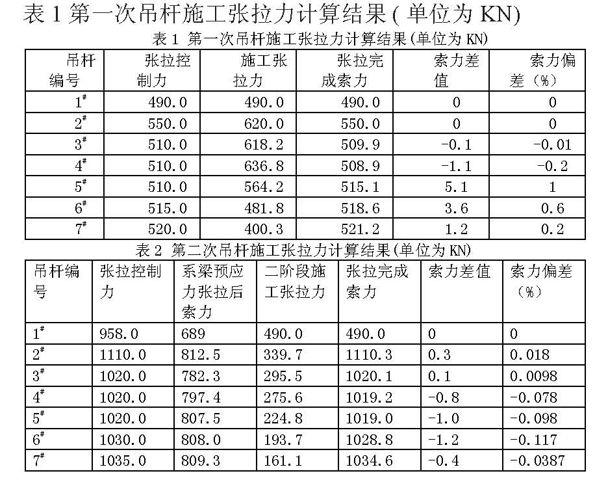
用迭代算法来求解吊杆施工张拉力值。首先解算出第一次张拉吊杆的施工张拉力值，然后解算出主梁预应力束张拉完成后，受到其影响后应有的二次吊杆张拉力值。其计算结果如表1和表2所示。

表1和表2的计算结果表明，已张拉的吊杆的吊杆力受到后张拉的的吊杆的影响已经较大，迭代算法是以张拉控制力值为目标值来进行迭代，可以求得满足精度的施工张拉力，使用迭代算法计算出来的张拉力进行张拉，可以避免后期繁琐的调索工作，使吊杆力一次达到张拉控制力的要求

结 论

系杆拱桥施工过程复杂，期间伴随着结构体系以及边界条件的变化，吊杆张拉是对结构体系进行转换的重要过程。为了减少后期索力调整工作，通过一次张拉使索力达到张拉控制力的值，本文采用迭代算法对工程实例进行了计算和验证，得到了比较理想的效果，大大减少了张拉吊杆的工作量。

参考文献

[1] 肖汝诚，项海帆.斜拉桥索力优化及其工程应用[J] .计算力学学报.1998（1）：118-126

[2] 李国平.连续拱梁组合桥的性能与特点[J].桥梁建设，1999（1）：11—13.

[3] 虞建成，邵容光，王小林.系杆拱桥吊杆初始张拉力及施工控制[J].东南大学学报，1998（3）：112-116.

[4] 彭宜茂.系杆拱桥吊杆初始张拉力的计算方法[J].水利水电科技进展，2000（12）：32—33.

[5] 张维国.再谈系杆拱桥吊杆初始张拉力的计算方法[J].水利水电科技进展，2003（3）：26—28.

[6] 黎静.连续梁拱组合体系结构柔性吊杆张拉力的确定[J].工程建设，2006，38（3）：30—32.