抛物型微分方程的多尺度有限元高效计算

江 山，易年余，孙美玲

（1.扬州大学数学科学学院，江苏 扬州225002；2.湘潭大学数学与计算科学学院，湖南 湘潭411105；3.南通职业大学基础课部，江苏 南通226007）

抛物型微分方程的多尺度有限元高效计算

江 山1*，易年余2，孙美玲1，3

（1.扬州大学数学科学学院，江苏 扬州225002；2.湘潭大学数学与计算科学学院，湖南 湘潭411105；3.南通职业大学基础课部，江苏 南通226007）

提出了抛物型微分方程的高效多尺度数值计算方法.与传统有限元基函数相比，多尺度有限元基函数能更好地反映问题自身的强振荡微观信息，结合多尺度有限元格式，可使计算结果在宏观尺度获得很好的数值逼近.对时间采用欧拉向后差分离散化，得到稳定且收敛的数值结果.新方法在取得高仿真逼近的同时，节约了大量计算资源和时间，因而更具应用价值.

抛物型模型；多尺度有限元；时间离散化；欧拉向后差分；算法效率

奇异摄动微分方程广泛应用于流体力学、热电传导、分子动力学、声光学等领域［1-2］，其特点是若存在小摄动参数ε，方程的解就会因在子区域剧烈变化而产生边界层现象［3］，使其在许多跨尺度问题中难以有效求解，故奇异摄动微分方程高效数值解法引起学者们的关注.Hou等［4］开创性地提出多尺度有限元法（multiscale finite element method，MsFEM），随后的理论研究和数值应用不断取得进展［5-8］.与时间、空间有关的多尺度抛物型微分方程是当今研究的热点和难点，人们试图在计算精度和计算代价之间寻求平衡，致力于探寻既能保证计算精度又可节约计算资源的新数值方法来处理复杂的时空多尺度问题.Efendiev等［9］提出了广义多尺度有限元法，采用在脱机空间计算基函数、在联机空间求解特征值的方法，实现了约化计算.Sun等［10］针对二维反应扩散方程，利用嵌入的多尺度格式并结合等级网格，仅在边界层粗单元采用多尺度基，在内部光滑粗单元采用传统有限元基，从而节约了大量的空间与时间.在本文中，笔者提出时间、空间的多尺度抛物型初边值问题：

式中u为真解，t为时间，kε（x）为强振荡系数，依赖于尺度参数ε（ε≪1），x为二维空间变量，f为右端函数，g为边值函数，u0为初值函数，Ω为空间域及边界∂Ω.在一定条件下，该问题是适定的，但缺少普遍适用性的解析式，故其高效的数值解是本文研究的重点.

1　传统有限元法与多尺度有限元法

1.1变分形式和有限元格式

问题（1）的变分形式是寻求u∈H1（Ω）满足

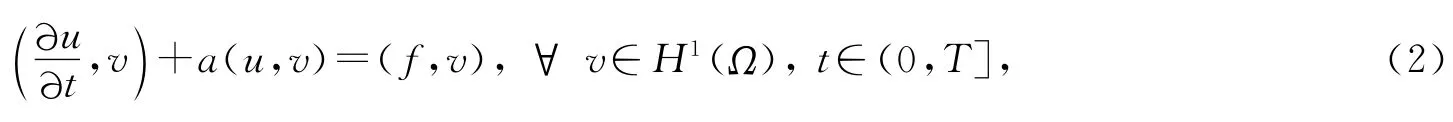
将二维区域Ω分为若干子区域Ωk，且∪Ωk=Ω.令Kh是矩形网格剖分，在每一个单元K∈Kh定义4个节点基函数及其对应的二维坐标［xi，xi+1］×［yj，yj+1］.由有限元的双线性标准基与等参变换可知：φ1=（1-ξ）（1-η），φ2=ξ（1-η），φ3=ξη，φ4=（1-ξ）η为4个基函数；ξ=（x-xi）/hx，η=（y-yj）/hy为等参变换；hx=xi+1-xi，hy=yj+1-yj为x，y 方向单元步长，且微分d x=hxdξ，d y=hydη，有

1.2多尺度有限元格式

采用新的多尺度有限元法处理时空抛物型问题时，对应的变分形式是寻求uh∈Uh满足

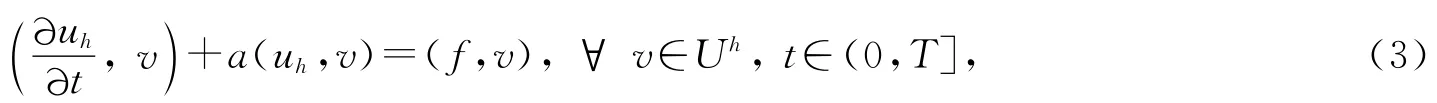
其中uh为多尺度有限元解，而多尺度空间Uh=span｛φi：i=1，…，4，∀K∈Kh｝是由多尺度基所生成的函数空间.

针对多尺度基函数，在粗网格单元K中求解子问题

给定线性边界条件，即i=j时φi（xj，yj）=1，i≠j时φi（xj，yj）=0，且φi（xj，yj）在∂K上呈线性变化.由于子问题（4）与原问题（1）具有相同的微分算子，故在粗网格K 中求得的多尺度基函数φi能自动反映宏观单元的微观信息，如尺度振荡性（见图1（a）），而不再是有限元的简单双线性基函数φi（见图1（b））.

图1　多尺度基函数（a）与有限元双线性基函数（b）的三维直观图Fig.1 The 3D mesh for multiscale basis functions（a）and standard basis functions（b），respectively

传统有限元法须在非常密的细网格上求解，二维空间全局节点数Nglobenode=（Nx×nx+1）×（Ny×ny+1），式中Nx，nx分别为x 方向上粗、细单元剖分数.而多尺度有限元法仅在粗网格上求解，其全局粗节点数为Ncoarsenode=（Nx+1）×（Ny+1），因此计算时所需的存储量和时间都大为缩减.

2　时间相关的全离散多尺度计算

针对原问题（1）的时间尺度离散，采用更有效的Euler向后差分隐格式

这样可依次求得不同时间间隔的多尺度数值解un+1h.

3　数值实验

图2　强振荡系数kε（x）Fig.2 The ploted oscillating coefficient kε（x）

图3　初值u0Fig.3 Initial value u0

计算程序用Matlab2012语言编写，传统有限元法在细网格上所需存储量为O（Nx×nx）2，而多尺度有限元在粗网格上仅需O（Nx）2的存储量.用R存储多尺度基函数及其对应的节点矩阵，其大小size（R）=Ncoarsenode×Nglobenode，即行、列数分别为全局粗、细节点数.细网格的有限元解用u=A-1F求解（计算时间较长）；而用多尺度有限元计算时，利用之前得到的M，A，F，即粗网格上的总质量矩阵Mms=R×M×R′，总刚度矩阵Ams=R×A×R′，总载荷向量Fms=R×F，则可用ums=A-1msFms很快算得多尺度有限元在粗网格上的解，再用umsfine=R′×ums还原得到多尺度有限元在细网格上的解，从而方便地比较2种数值算法的精度.

令每步时间间隔Δt=0.001 s，迭代20步的计算结果见图4.结果表明，迭代20步后有限元解与多尺度有限元解数值模拟效果非常接近.但前者是在非常密的细网格上运算得到，计算存储量和计算时间都很大；而后者仅在较粗网格上运算，节约了大量的计算资源并获得很好的数值仿真结果.

图4　迭代20步时抛物型问题的传统有限元解（a）与多尺度有限元解（b）之比较Fig.4 The standard FEM solution（a）and the MsEFM solution（b）for the parabolic problem after 20 steps，respectively

L2范数的绝对误差和相对误差分别为

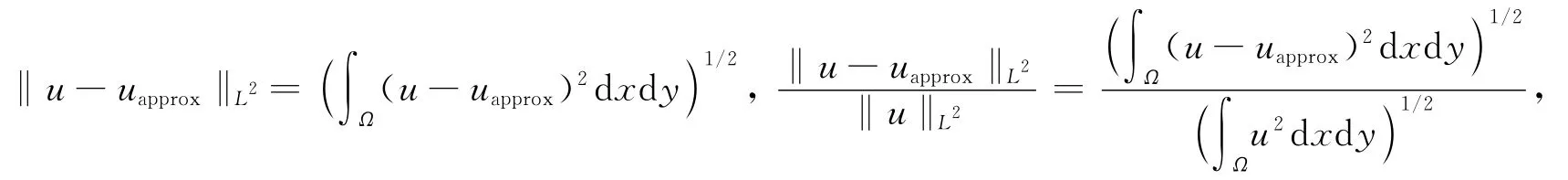
其中u表示真解，uapprox表示2种方法对应的数值解，其值的大小可作为度量的依据（见图5）.从图5可以看出抛物型问题的MsFEM解随时间步增加具有数值稳定性和收敛性的特征.数值算例很好地验证了多尺度有限元模拟可以高效处理时空多尺度抛物型微分方程，该方法能在计算精度和计算代价之间取得理想的平衡，具备广阔的数值应用优势.

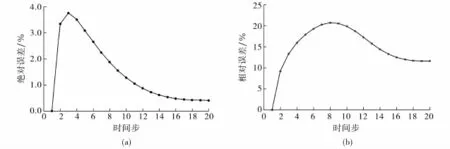
图5　抛物型多尺度有限元解随时间变化L2范数的绝对误差（a）与相对误差（b）Fig.5 The L2absolute error（a）and relative error（b）of the MsFEM parabolic solutions varying with time

［1］CAI Xin，CAI Danlin，WU Ruiqian，et al.High accuracy non-equidistant method for singular perturbation reaction-diffusion problem［J］.Appl Math Mech，2009，30（2）：175-182.

［2］SU Fang，XU Zhan，CUI Junzhi，et al.Multiscale computation method for an advection-diffusion equation［J］. Appl Math Comput，2012，218（14）：7369-7374.

［3］DENG Weibing，YUN Xulai，XIE Chunhong.Convergence analysis of the multiscale method for a class of convection-diffusion equations with highly oscillating coefficients［J］.Appl Numer Math，2009，59（7）：1549-1567.

［4］HOU T Y，WU Xiaohui.A multiscale finite element method for elliptic problems in composite materials and porous media［J］.J Comput Phys，1997，134（1）：169-189.

［5］YUE Xingye，E Weinan.The local microscale problem in the multiscale modeling of strongly heterogeneous media：effect of boundary conditions and cell size［J］.J Comput Phys，2007，222（2）：556-572.

［6］JIANG Lijian，PRESHO M.A resourceful splitting technique with applications to deterministic and stochastic multiscale finite element methods［J］.Multiscale Model Simul，2012，10（3）：954-985.

［7］DENG Weibing，WU Haijun.A combined finite element and multiscale finite element method for the multiscale elliptic problems［J］.Multiscale Model Simul，2014，12（4）：1424-1457.

［8］孙美玲，江山，唐元生.多尺度有限元法在Shishkin边界层的数值模拟［J］.扬州大学学报：自然科学版，2014，17（2）：25-28，32.

［9］EFENDIEV Y，GALVIS J，HOU T Y.Generalized multiscale finite element methods（GMsFEM）［J］.J Comput Phys，2013，251：116-135.

［10］SUN Meiling，JIANG Shan.Multiscale basis functions for singular perturbation on adaptively graded meshes［J］.Adv Appl Math Mech，2014，6（5）：604-614.

The multiscale finite element computation for
efficiently solving the parabolic differential equation

JIANG Shan1*，YI Nianyu2，SUN Meiling1，3
（1.Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China；2.Sch of Math&Comput Sci，Xiangtan Univ，Xiangtan 411105，China；3.Dept of Fundam Courses，Nantong Vocat Coll，Nantong 226007，China）

An efficient multiscale finite element computation is proposed to solve the time-space parabolic problems.By comparing the standard finite element basis functions with the multiscale basis functions，the latter has the ability to reflect the local oscillating information，and by the multiscale finite element scheme it may achieve good approximation on the macroscopical scale.For time scale to apply the Euler backward difference discretization，the author demonstrates the stability and convergence by the numerical experiment.This new method obtains the good simulation，and at the same time it saves plenty of computer resource and time，as a consequence it is available for further application values.

parabolic model；multiscale finite element；time discretization；Euler backward difference；algorithm efficiency

O 241.82

A

1007-824X（2015）02-0026-05

（责任编辑 秋 实）

2014-10-28.*联系人，E-mail：jiangshan@yzu.edu.cn.

国家自然科学青年基金资助项目（11301462）；江苏省高校自然科学基金资助项目（13KJB110030）；江苏省高校研究生科研创新资助项目（KYLX-1332）；扬州大学博士后研究资助项目；扬州大学新世纪人才工程资助项目.

江山，易年余，孙美玲.抛物型微分方程的多尺度有限元高效计算［J］.扬州大学学报：自然科学版，2015，18（2）：26-30.