p元m序列的三值互相关分布
梁 华,陈文兵,罗金权,唐元生*
(1.扬州大学数学科学学院,江苏 扬州225002;2.淮阴师范学院数学科学学院,江苏 淮安223300)
p元m序列的三值互相关分布
梁 华1,2,陈文兵1,罗金权1,唐元生1*
(1.扬州大学数学科学学院,江苏 扬州225002;2.淮阴师范学院数学科学学院,江苏 淮安223300)
设m,k是正整数,e=(m,k)且m/e,k/e均为奇数,p是满足pe≡1(mod4)的奇素数,d=(pm+1)·(pk+1)/4.确定了指数和的值分布,并给出周期为pm-1的p元m序列{st}及其采样序列{sdt}之间的互相关函数的值分布.
m序列;互相关性;指数和;二次型
具有低相关性的序列在CDMA通信系统中有重要的应用.多年来,周期为pm-1的p元m序列{st}及其采样序列{sdt}之间的互相关性得到了广泛关注[1-5].序列的互相关性的值分布可转化为相应指数和的值分布.对于满足p≡3(mod4)的奇素数p,奇数n及 d1=1,d2=(pn+1)/(p+1)+(pn-1)/2,Xia等[6]给出了指数和S(α,β)的值分布.对于同样条件的奇素数p与奇数n,Choi等[7]研究了d1=1,d2=(pn+1)/(pk+1)+(pn-1)/2且k|n情形下指数和S(α,β)的值分布,并给出构造的新序列集的互相关值的上界.对满足m/(m,k)是奇数,k/(m,k)是偶数的正整数m,k及满足pm≡1(mod4)的奇素数p,Liang等[8]研究了d1=(pm+ 1)(pk+1)/4,d2=1情形下指数和S(α,β)的值分布,并给出相应的应用.在本文中,笔者拟利用有限域上二次型理论,在文献[8]的基础上,对满足k/(m,k)是奇数的指数和作进一步探讨,进而研究周期为pm-1的p元m序列{st}及其采样序列{sdt}之间的互相关性,并给出互相关函数的值分布.
1 预备知识
设m,k是正整数,e=(m,k)且m/e,k/e均为奇数;p 是满足pe≡1(mod4)的奇素数,q0=pe,q=pm=qs0,其中s=m/e;GF(pi)表示含有pi个元素的有限域,GF(pi)*=GF(pi)\{0};对于i|j,表示GF(pj)到GF(pi)的迹映射;g是GF(pm)的一个本原元.记d=(pm+1)(pk+1)/4,对于周期为pm-1的p 元m 序列{st},其中之间的互相关函数定义为
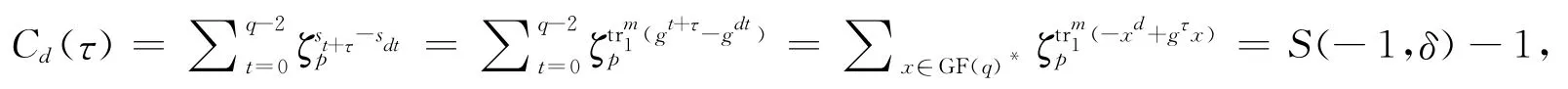
其中δ=gτ(0≤τ≤q-2),由Cd(τ)定义知,互相关分布{Cd(τ)|0≤τ≤q-2}可由S(-1,β)(β∈GF(q)*)的值分布得到.
设λ是GF(q0)中的非平方元,由m/e,k/e均为奇数及pe≡1(mod4)知,λ也是GF(q)中的非平方元且λd=λ.当x跑遍GF(q)*中所有元素时,x2,λx2分别跑遍GF(q)*中所有平方元和非平方元各2次,于是
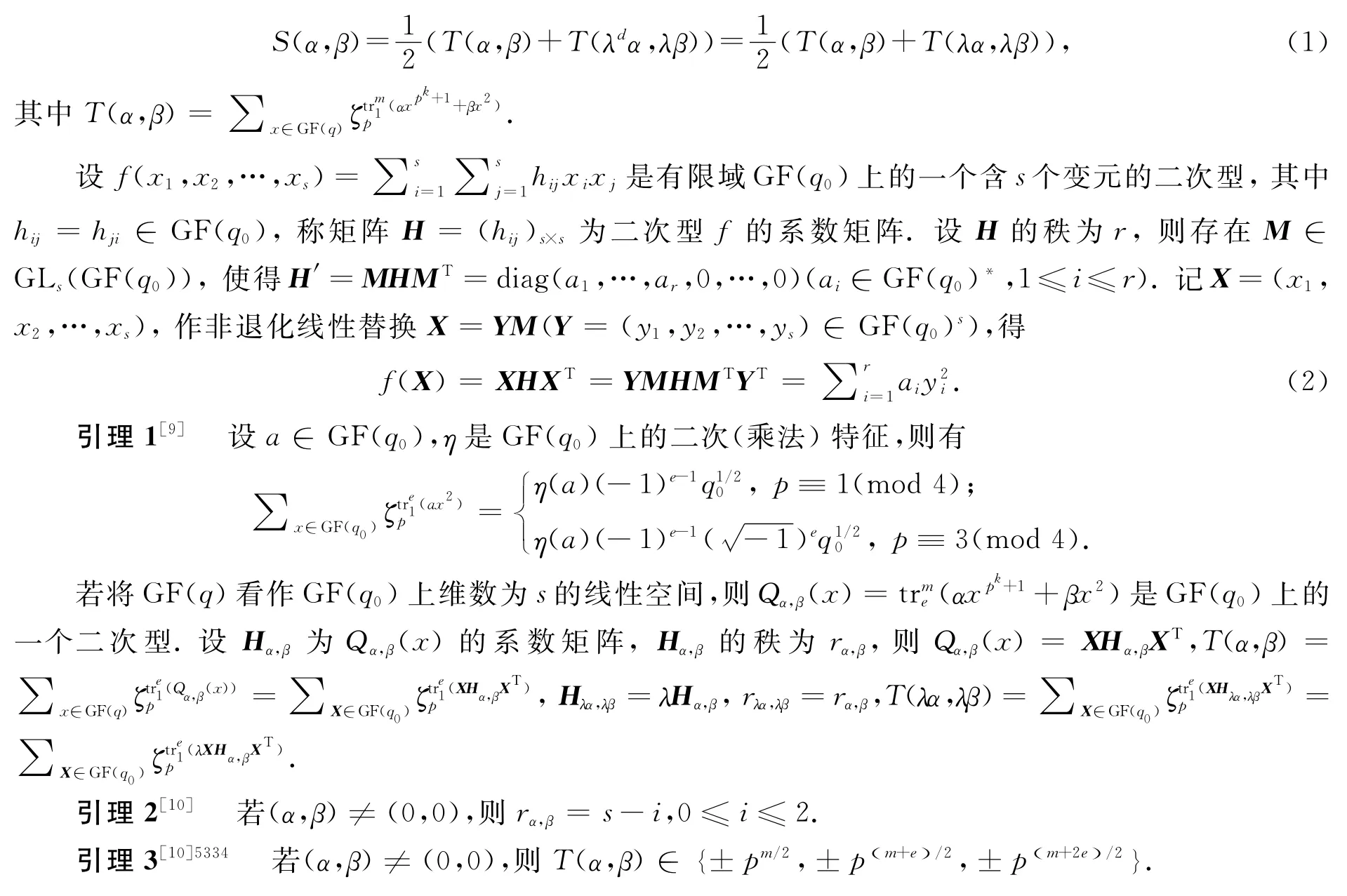
2 主要结果

[1]陈文兵,唐元生,罗金权.p元m序列与其采样序列的互相关性[J].扬州大学学报:自然科学版,2014,17(4):12-15.
[2]TRACHTENBERY H M.On the cross-correlation functions of maximal linear recurring sequences[D].Los Angeles,CA:Univ Southern California,1970.
[3]HELLSETH T.Some results about the cross-correlation function between two maximal linear sequences[J]. Discr Math,1976,16(3):209-232.
[4]DOBBERTIN H,FELKE P,HELLESETH T.Niho type cross correlation functions via Dickson polynomials and Kloosterman sums[J].IEEE Trans Inf Theory,2006,52(2):613-627.
[5]LUO Jinquan,HELLESETH T,KHOLOSHA A.Two nonbinary sequences with six-valued cross correlation[C]//2011 Fifth International Workshop on Signal Design and its Applications in Communications.Guilin:IEEE,2011:44-47.
[6]XIA Yongbo,ZENG Xiangyong,HU Lei.Further crosscorrelation properties of sequences with decimation factor[J].Appl Algebra Eng Commun Comput,2010,21(5):329-342.
[7]CHOI S T,KIM Y S,NO J S.On the cross-correlation of a p-ary m-sequence and its decimated sequences by[J].IEICE T Commun,2013,96(9):2190-2197.
[8]LIANG Hua,TANG Yuansheng.The cross correlation distribution of a p-ary m-sequence of period pm-1 and its decimated sequences by d=(pk+1)(pm+1)/4[J].Finite Fields Appl,2015,31:137-161.
[9]LIDL R,NIEDERREITHER H.Finite fields[M].Boston:Addison-Wesley,1983:278-289.
[10]LUO Jinquan,FENG Keqin.On the weight distribution of two classes of cyclic codes[J].IEEE Trans Inf Theory,2008,54(5):5332-5344.
p-ary m-sequences with three-valued cross-correlation
LIANG Hua1,2,CHEN Wenbing1,LUO Jinquan1,TANG Yuansheng1*
(1.Sch of Math Sci,Yangzhou Univ,Yangzhou 225002,China;2.Sch of Math Sci,Huaiyin Norm Univ,Huai’an 223300,China)
Let m,k be two positive integers with e=(m,k),m/e and k/e are odd,p be an odd prime with pe≡1(mod 4),d=(pm+1)(pk+1)/4.The value distribution of the exponential sumis determined,and the cross-correlation between a p-ary m-sequence{s}of
m-sequence;cross-correlation;exponential sum;quadratic form
O157.4
A
1007-824X(2015)02-0015-03
(责任编辑 何青玉)
2014-12-26.*联系人,E-mail:ystang@yzu.edu.cn.
国家自然科学基金资助项目(61379004).
梁华,陈文兵,罗金权,等.p元m序列的三值互相关分布[J].扬州大学学报:自然科学版,2015,18(2):15-17,25.
tperiod pm-1 and its decimated sequence{sdt}is given.

