单位群U(z[])的结构
刘兴鹏,陈佳慧,李立斌
(扬州大学数学科学学院,江苏 扬州225002)
刘兴鹏,陈佳慧,李立斌*
(扬州大学数学科学学院,江苏 扬州225002)
利用整环的单位与Pell方程解的关系,给出了同底的非平方自然数n对应的整环的单位群及其亚生成元之间的关系.
整环;单位群;Pell方程
设I为一个有单位元1环,非零元ε∈I称为I的单位,若ε是I中的乘法可逆元,即∃ε′∈I使得εε′=1.容易验证集合U(I)={ε∈I|ε是I的单位}关于I的乘法构成一个群,称此群为I的单位群.目前,对于单位群结构的研究多见于矩阵环[1]、群环[2-4]、结合代数[5-6]等.例如,Khan等[3]106给出了单位群U(FS4)的性质,Halasi[7]描述了Dn代数单位群的一些特征,屈寅春等[8]证明了单位元群是素数阶循环群直和的剩余类环,Davis等[9]给出了有限单群是单位群的条件.本文主要根据数论和近世代数基本理论,利用整环中的单位与Pell方程解的关系对整环单位群的结构进行研究.
1 单位的充要条件

其中n为非平方自然数.
定理1[10]中的单位的充要条件是x,y满足方程x2-ny2=1或x2-ny2= -1.
2 单位群的结构
定义2 Pell方程(1)(2)中满足x>0,y>0的解称为正解.
由文献[11]可知,存在方程(1)或(2)的正解(x1,y1),使得方程x2-ny2=±1的任意解(x,y)可由
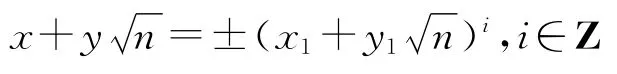
确定.于是,方程x2-ny2=±1的解完全由正解(x1,y1)所确定,则称此正解为最小正解,从而得出下面的定理.

3 单位群间的关系


[1]JANEZ S.Lifting units in clean rings[J].J Algebra,2013,381(1):200-208.
[2]HERTWECK M,HÖFERT C R,KIMMERLE W.Finite groups of units and their composition factors in the integral group rings of the groups PSL(2,q)[J].J Group Theory,2009,12(6):873-882.
[3]KHAN M,SHARMA R K,SRIVASTAVA J B.The unit group of FS4[J].Acta Math Hungar,2008,118(1/2):105-113.
[4]KIMMERLE W.Unit groups of integral group rings:old and new[J].Jahresber Dtsch Math-Ver,2013,115(2):101-112.
[5]TANG Gaohua,WEI Yangjiang,LI Yuanlin,et al.Unit groups of group algebras of some small groups[J]. Czech Math J,2014,64(1):149-157.
[6]GILDEA J.Units of group algebras of non-abelian groups of order 16 and exponent 4 over F F2k[J].Results Math,2012,61(3/4):245-254.
[7]HALASI Z.On the characters of the unit group of DN-algebras[J].J Algebra,2006,302(2):678-685.
[8]屈寅春,杨一超,李立斌.单位元群是素数阶循环群直和的剩余类环[J].扬州大学学报:自然科学版,2010,13(3):1-4.
[9]DAVIS C,OCCHIPINTI T.Which finite simple groups are unit groups[J].J Pure Appl Algebra,2014,218(4):743-744.
[11]潘成洞,潘成彪.初等数论[M].北京:北京大学出版社,2005:355-360.
The structure of unit group U(z[])
LIU Xingpeng,CHEN Jiahui,LI Libin*
(Sch of Math Sci,Yangzhou Univ,Yangzhou 225002,China)
By using the relationship between the unit group of domain z[]and the solution of Pell equation,the author considers some structures of unit groups of domain z[]under the framework of the quasi-generators,where n has the same-based non-square natural numbers.
domain;unit group;Pell equation
O153.3;O154
A
1007-824X(2015)02-0005-03
(责任编辑 林 子)
2014-04-15.*联系人,E-mail:lbli@yzu.edu.cn.
高等学校博士点基金资助项目(20123250110005);全国大学生科技创新基金资助项目(201311117029Z).
刘兴鹏,陈佳慧,李立斌.单位群U(z[])的结构[J].扬州大学学报:自然科学版,2015,18(2):5-7,11.

