“圆”来如此——巧用轨迹圆解题举隅

●江苏省淮安市淮海中学 王开林

“圆”来如此
——巧用轨迹圆解题举隅

●江苏省淮安市淮海中学 王开林

圆，一中同长也.即平面内与定点的距离等于定长的点的轨迹是圆.数学家阿波罗尼斯发现：平面内与两个定点的距离之比为不等于1的正数的点的轨迹也是一个圆.在解题中也常会遇到许多轨迹是圆的问题，下面笔者结合具体的示例谈谈自己教学的体会.

一、阿波罗尼斯圆：平面内与两个定点的距离之比为不等于1的正数的点的轨迹是一个圆

例1 （2013年高考江苏第17题）如图，在平面直角坐标系xOy中，点A（0，3），直线l：y=2x-4，设圆C的半径为1，圆心在l上．

（1）若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；

（2）若圆C上存在点M，使|MA|=2|MO|，求圆心C的横坐标a的取值范围．

化简得：x2+（y+1）2=4，即：点M的轨迹是以（0，-1）为圆心、2为半径的圆，可记为圆D．

又因为点M在圆C上，故圆C与圆D的关系为相交或相切．

评析：点M的轨迹是一个阿波罗尼斯圆，运用交轨法可将问题转化为两圆位置关系问题来解决.

二、若过椭圆上两点的切线互相垂直，则这两条切线的交点的轨迹是一个圆

（1）求椭圆C的标准方程；

（2）若动点P（x0，y0）为椭圆C外一点，且过点P的椭圆C的两条切线相互垂直，求点P的轨迹方程.

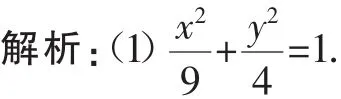
（2）设两切线为l1、l2，

①当l1⊥x轴或l1∥x轴时，对应的l2∥x轴或l2⊥x轴，可知P（±3，±2）.

因为点P（±3，±2）满足上式，综上知点P的轨迹方程为x2+y2=13.

评析：此题的结论可推广到一般情况：若过椭圆上两点的切线互相垂直，则这两条切线的交点的轨迹是一个圆.

三、平面内到两个定点A、B的距离的平方之和为定值点的轨迹是圆

例3（2015年徐州三模第12题）在平面直角坐标系xOy中，已知圆C：（x-a）2+（y-a+2）2=1，点A（0，2），若圆C上存在点M，满足|MA|2+|MO|2=10，则实数a的取值范围是_______.

解析：设点M（x，y）.

由|MA|2+|MO|2=10，得x2+y2+x2+（y-2）2=10，整理得：x2+（y-1）2=4.由题意知两圆有公共点，则R-r≤d≤R+r，即1≤a2+（a-3）2≤32，解得0≤a≤3.

评析：满足|MA|2+|MO|2=10的点M的轨迹是一个圆，运用交轨法可将问题转化为两圆的位置关系问题来解决.

四、直角三角形的直角顶点在一个定圆内，另外两个顶点在圆上，斜边的中点的轨迹是一个圆

例4（2014年常州市高三数学试题第14题）在平面直角坐标xOy中，已知圆O：x2+y2=16，点P（1，2），M、N为圆上不同的两点，且满足的最小值为______.

轨迹为圆的问题在此无法一一列举，通过以上几道例题，我们可以清楚地看到利用轨迹圆来解题，可以化繁为简，事半功倍.A