浅谈有效思维课堂的构建——以《直线与抛物线的位置关系》一课教学为例

杨 玲



浅谈有效思维课堂的构建——以《直线与抛物线的位置关系》一课教学为例

杨 玲

（延边第二中学，吉林 延吉 133000）

构建有效思维课堂符合“以教师为主导、以学生为主体”的教学理念要求教师努力创设学生乐思、乐学的情境，把学生引入积极的思维状态中，引导学生自主学习、自主参与、自主探究，帮助学生主动构建知识，提高课堂效率。

高中教学；有效思维课堂；构建；问题情境；自主学习

随着课程改革的不断深入,作为一线的数学教师,越来越深刻地感受到，构建有效数学教学首先应该解决这些问题：怎样让学生在这堂课上有浓厚的兴趣？怎样提问才能引导学生积极思考，更容易接受？怎样培养学生解决问题的能力？这些问题其实可以归结为一个问题，即如何构建数学有效思维课堂。

一、设计一系列有梯度的问题激发学生求知欲，促进学生有效思维

著名数学教育家弗赖登塔尔有一个重要的观点：“教数学就必须教相互连贯的材料，而不是孤立的片断。在设计本节课的时候应突出整堂课是由一个个问题连接的知识链组成的，问题设计逐层递进，以问题“直线与双曲线有哪些位置关系，交点个数分别是多少” 引入课题，学生回顾旧知，教师演示几何画板，如图1。

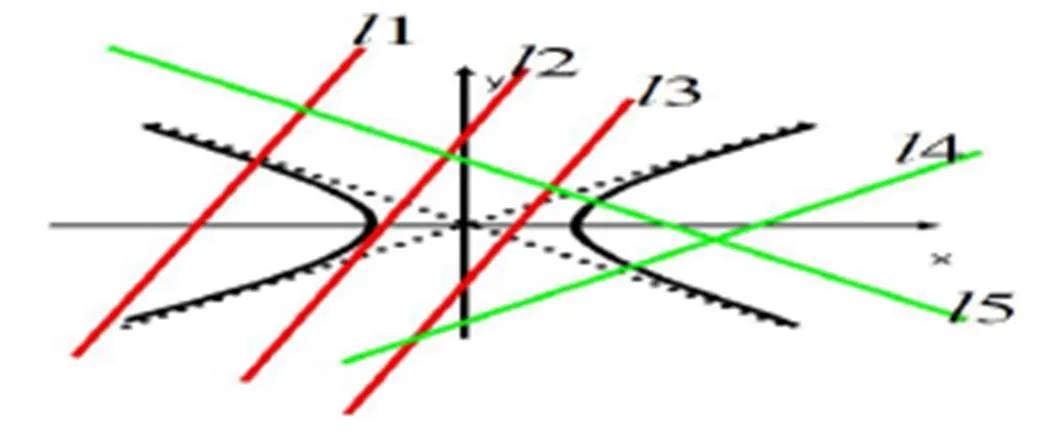
图1

首先通过问题“如何判断位置关系”让学生思考以前判断位置关系的常用方法即解析法：

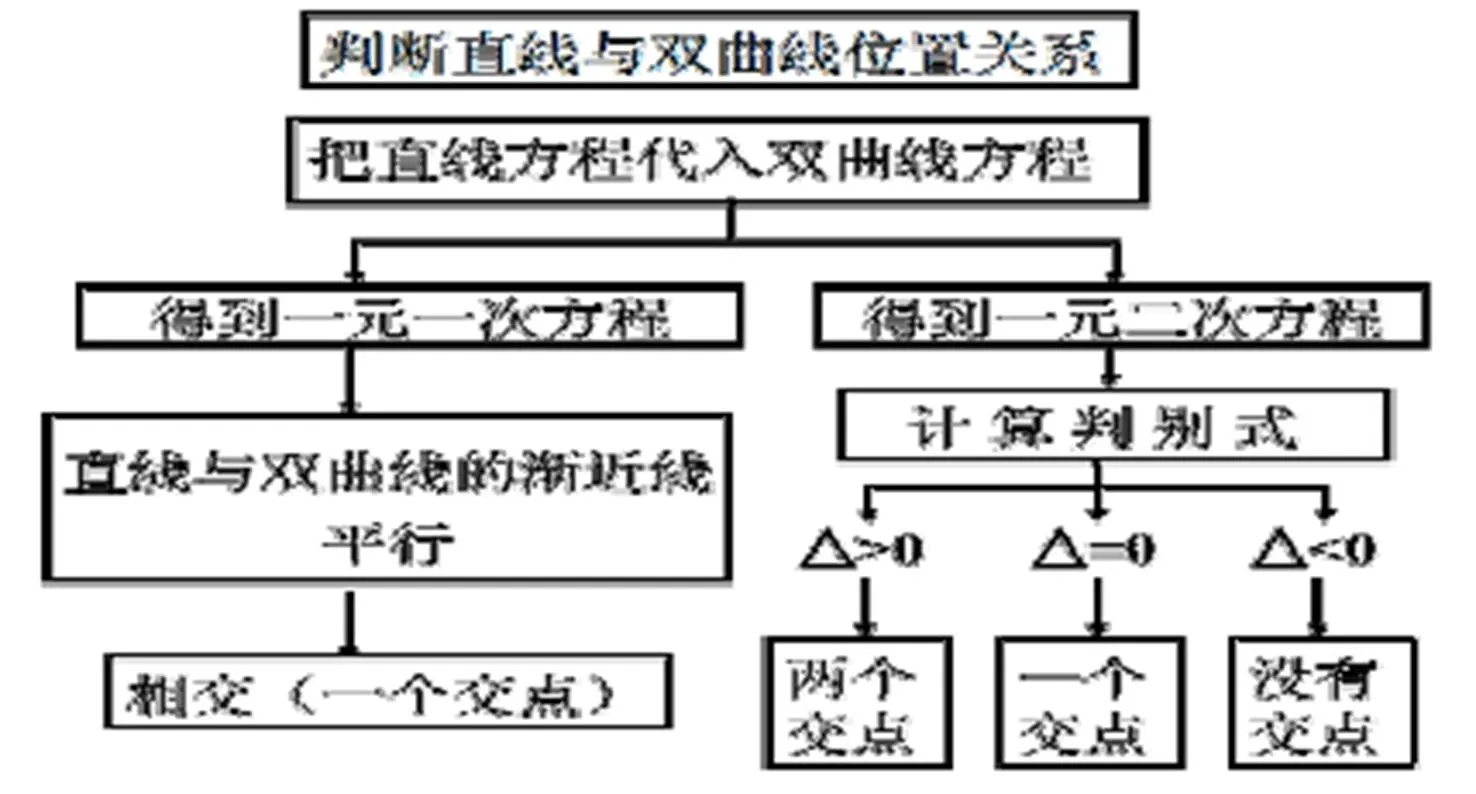
其次以问题“类比直线与双曲线的位置关系，猜想一下直线与抛物线的位置关系呢” 展开直线与抛物线位置关系探讨，这里可以让学生作图猜想位置关系，让一位同学把自己的图形演示给大家。

学生从图形的直观感知再到问题的探究，这样做更符合学生的认知规律，学生从心理上产生情感共鸣，激发学生求知欲，提高课堂效率。

然后以问题“以一个具体的实例来探讨它们的位置关系”引入新课，例题如下：

例1：已知抛物线C：y2=4x，直线l过定点A（-1,0），斜率为k，判断l与C有几个交点，并计算相应的k的取值范围。

本底资料为2013年国家下发的1∶250 000 DLG数据，更新资料为2017年更新完成的云南省1∶50 000 DLG数据库[1]。

学生带着疑问去学习，造成学生心理上的悬念，唤起学生的求知欲和探索的欲望。

二、创设探究型情境，促进学生发散思维

在设计教学方案时，可以不用照搬教材中的例题，把教材上的知识点改编成需要学生探究的问题，即创设探究型情境，激发学生的探究兴趣。

根据苏联著名心理学家维果茨基的“最邻近发展区”理论，在学生回答例1后，可以设计以下三个变式：

变式1：将例1中的“斜率为k”去掉，判断交点情况。

引导学生思考探究斜率不存在时，直线与抛物线的位置关系。

教师提问：“刚才我们用解析法完成例1，如何从图形的角度来分析例1呢？”诱导学生从另一个角度即几何角度分析位置关系，教师利用几何画板动态演示，如图2，动直线l在绕着定点A旋转的过程中，其交点情况学生可以一目了然。

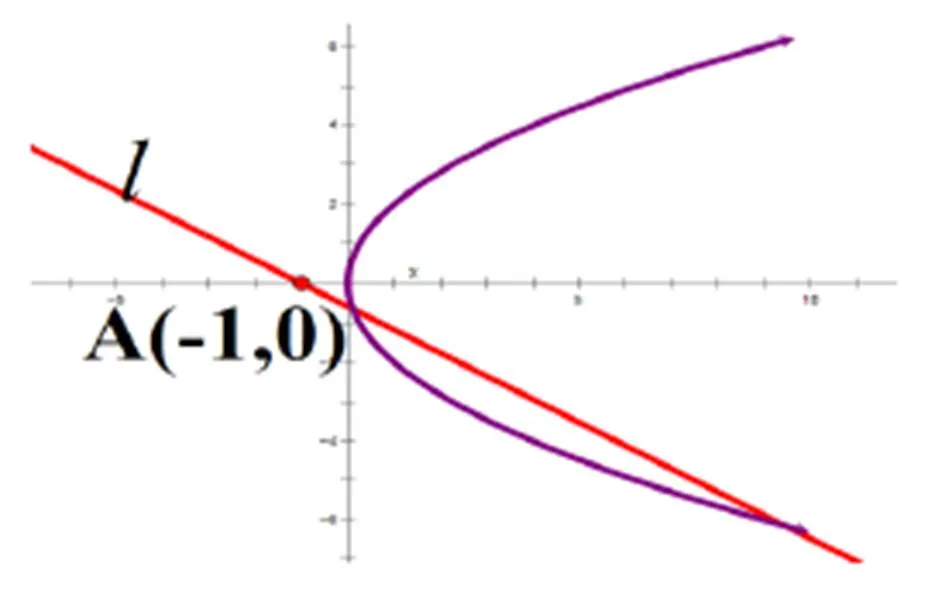
图2

图3

接下来教师提问：“定点A在抛物线外，我们发现过定点A且与抛物线有一个交点的直线有三条（如图3），那么是不是只要定点在抛物线外，那么过定点且与抛物线有一个交点的直线肯定有三条呢？”通过这个问题，定点的特殊性扩展到了一般性，这样更加符合学生认识事物从特殊到一般的规律，使他们对知识产生浓厚的兴趣。

变式2：将例1中的“A点改为B（1,2）（如图4）”，动直线l在绕着定点B旋转判断，交点情况、直线与抛物线有几种位置关系。

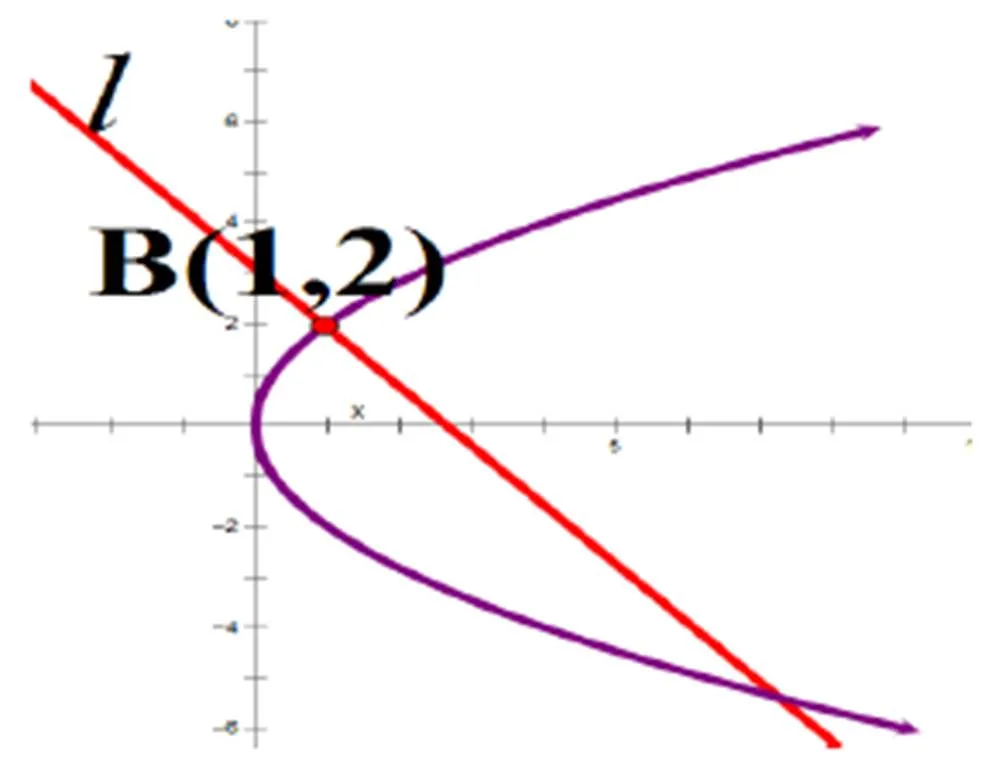
图4

图5

教师提问：“定点在抛物线上，过定点且与抛物线有一个交点的直线有几条？”

通过变式2，学生探究定点在抛物线上时，学生发现过点B且与抛物线有一个交点的直线有两条（如图5），两个交点和没有交点的情况也一目了然。

变式3：将例1中的“A点改为C(1,0)（如图6）”，动直线l在绕着定点C旋转，则交点情况？直线与抛物线有几种位置关系？

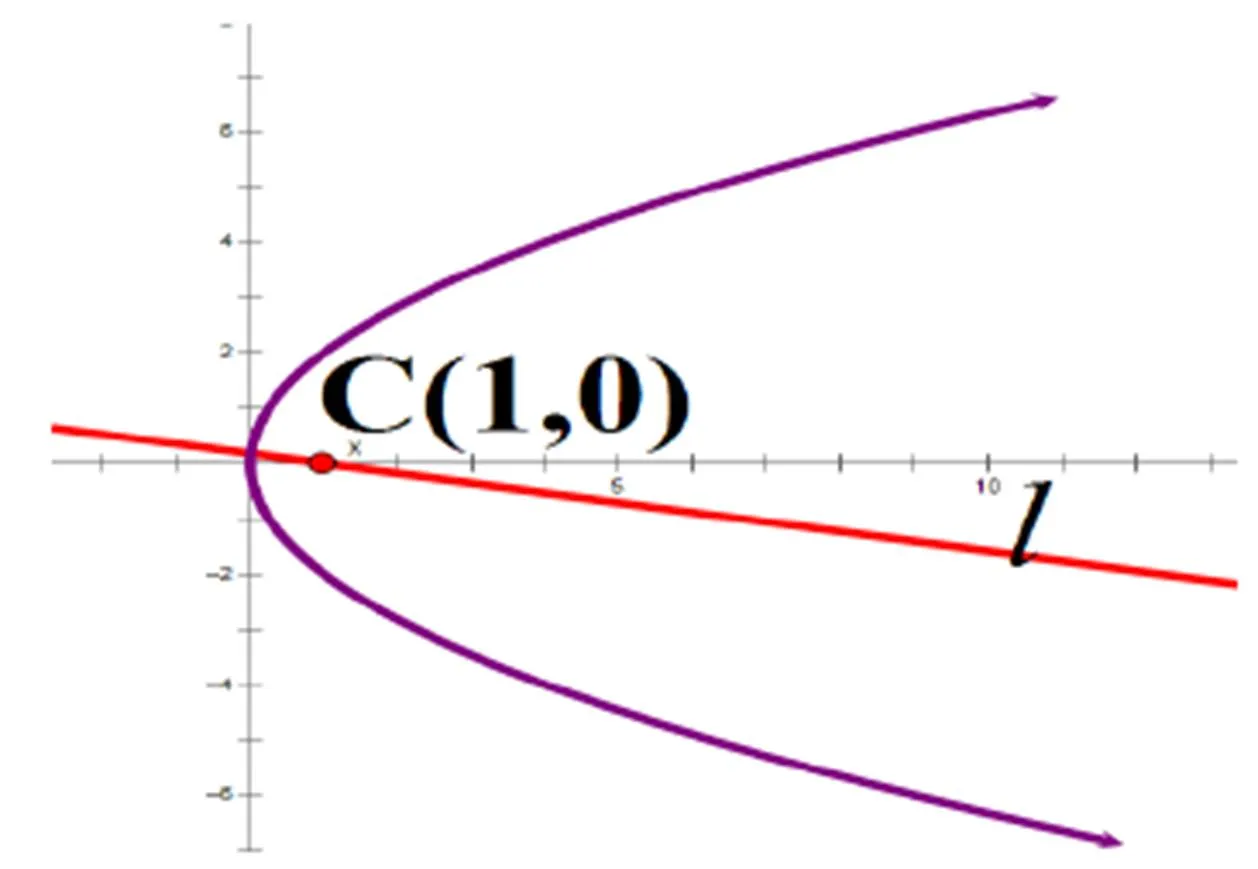
图6

图7

同变式2，教师提问：“定点在抛物线内，过定点且与抛物线有一个交点的直线有几条？”

通过变式3，学生探究定点在抛物线内时，学生发现过点C与抛物线有一个交点或两个交点，而与抛物线有一个交点的直线有一条（如图7），其余情况有两个交点。

通过设计探究型问题情境，学生从解析角度分析斜率存在过定点的直线与抛物线的位置关系；到斜率不存在的直线与抛物线的位置关系；到几何角度分析过抛物线外定点的直线与抛物线的位置关系；到几何角度分析过抛物线上定点的直线与抛物线的位置关系；到几何角度分析过抛物线内定点的直线与抛物线的位置关系。将例题发散，学生思维从点发散，到面、再到体，使学生多角度认识问题，进一步理解了所学知识，培养了学生的发散思维能力。

三、设计巩固重点的练习，从不同角度对知识加深理解，发展数学思维

学生在学习新知识之后，为了加强记忆，需要设计有针对性的强化练习:

1.已知抛物线的方程为y2=4x

（1）若直线l过定点F(4,2)，则直线与抛物线有一个交点的直线有___条；

（2）若直线l过定点M(4,4)，则直线与抛物线有一个交点的直线有___条；

（3）若直线l过定点N(0,1)，则直线与抛物线有一个交点的直线有___条；

2.上题（3）中直线方程分别是什么？

3.已知抛物线y2=8x的准线与x轴交于点Q，过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是______。

A.[-1/2,1/2] B.[-2,2] C.[-1,1] D.[-4,4]

学生发现练习1可以不用计算，只需利用图像就能解决，考察了几何角度判断直线与抛物线位置关系的方法，同时也巩固了“定点在抛物线外、上、内时，过定点的直线与抛物线有一个交点的直线条数”的知识点；而练习2在练习1的基础上求直线方程分别是什么，学生发现单纯从几何角度是解决不了的，需要借助于解析角度判断位置关系，复习巩固了解析法判断位置关系的步骤。

引导学生通过练习总结解析法和几何法解决位置关系的特点：解析法更加精确，但不直观；几何法直观，但不具体。实际做题时，可以将二者的结合，实现数和形的有效结合。设计练习3学生发现既可以用纯解析法解决，也可以用数形结合的方法解决，更加深刻的体会数形结合思想。

四、及时引导学生总结，培养成反思省的思维习惯

学生养成及时总结的习惯，不仅有利于提高记忆效果，使学生正确理解的知识及时留下深刻的印象，还能使错误理解的知识在教师指导下得到及时纠正，达到强化、巩固、加深理解的作用。所以教师引导学生及时总结非常重要。

在这节课开始教师引导学生总结直线与双曲线的位置关系判断方法，起到习旧引新的作用；在讲解完例题和变式1后，引导学生总结从解析角度分析直线与抛物线位置关系的步骤；在利用几何画板演示变式2和变式3后，引导学生总结定点在抛物线外、上、内时，过定点的直线与抛物线只有一个交点的直线有几条；在做练习时，引导学生总结解析法和几何法判断位置关系的优劣性，体会数形结合的思想；在课堂结束后，引导学生总结本节课知识点和涉及到的数学思想。

故教师引导学生及时总结，能够让学生对所学的数学知识有一个质的飞跃，能从多角度、多层次、多侧面地思考问题，对知识达到更深刻的理解，准确地运用解题方法，深刻体会运用的数学思想。

总之，构建有效思维课堂符合“以教师为主导、以学生为主体”的教学理念，学生可以进行积极地思考，促进自身思维的有效发展，易于激发学生学习的信心和勇气，提高课堂的有效性。

[1]孙玉恒,李 宁.双互动四统一教学范式再探析[J]延边教育学院学报,2010(6).

[2]何小亚,姚 静.中学数学教学设计[M].北京:科学出版社,2008.

[3]余文森.有效教学十讲[M].上海:华东师范大学出版社,2009.

[4]张玉彬.理想课堂的构建与实施[M].重庆:西南师范大学出版社，2010.

2015—04—24

G633.33

A

1673-4564（2015）03—0136—04