基于下垂控制的孤岛检测方法及其改进策略

贺 超，王 冕，陈国柱

（浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

孤岛效应是指电网失压时电源仍保持对失压电网中的某一部分线路继续供电的状态。非计划性孤岛现象会对人和设备造成严重危害［1-2］，因此，国内外对孤岛检测展开了广泛的研究。孤岛现象的检测方法主要可以分为三大类：被动检测方法、主动检测方法和开关状态监测方法。目前并网逆变器的孤岛检测策略一般都采用被动式检测方法与一种主动式检测方法相结合的方式进行。

被动式检测方法的基本思想是根据电网失电后逆变器输出端电压的幅值、频率、相位或谐波含量的变化进行孤岛效应检测［3］，具有简单、容易实现、对电能质量无影响等优点。但当逆变器输出功率与本地负载功率接近或平衡时，此方法将失效，因而存在较大的检测盲区［4］。

主动式孤岛检测方法通常采用人为对逆变器输出功率、频率或相位施加一定的扰动，电网正常工作时，由于电网的平衡作用，检测不到这些扰动；一旦电网出现故障，逆变器输出的扰动将快速累积并超出允许范围，从而检测到孤岛效应。主动式孤岛检测方法主要有有功电流扰动法［5］、无功电流扰动法［6-7］、谐波电流注入法［8］、谐波畸变率正反馈法［9-10］、电压正反馈法［11-14］、负序电压正反馈法［15］、滑模频率漂移法［16］、有源频率漂移法及其改进算法［17-23］、主动移相法［24］及其他方法［25-30］。以上所提及的主动式孤岛检测方法大多存在稳态运行时会对输出电能质量产生影响的问题；另外，功率扰动法，包括有功电流扰动法、无功电流扰动法、谐波电流注入法，在多个系统并联时将不再适用；电压正反馈法受输出功率、参数设计不当等因素影响会引起检测失败；滑模频率偏移法和有源频率偏移法会因RLC负载谐振频率的干扰产生漏判的情况；基于下垂特性锁相环的反孤岛策略［28-29］适应性受逆变器功率因数影响明显，且存在较大盲区；而其他方法也存在设计复杂、需要额外加入辅助电路等不足。

由于能够实现各个逆变器间的功率平衡，下垂控制在并网逆变器发电等相关领域得到了广泛应用［31-32］。本文结合孤岛控制算法自身特点，提出了一种基于下垂控制的孤岛检测算法及其改进策略，其在稳态时对输出电能质量无影响，同时适用于多逆变器并联应用。仿真结果验证了该算法的有效性。

1 下垂控制原理

下垂控制［33］的基本原理可以描述为：

其中，ω为逆变器输出角频率指令；ω*为逆变器空载输出电压角频率，即电网基波角频率；P*和P分别为逆变器有功功率指令和实际有功输出；U为逆变器输出电压幅值指令；U*为电网基波电压幅值；Q*和Q分别为逆变器无功功率指令和实际无功输出；m和n分别为下垂控制中逆变器输出电压的角频率和幅值下垂系数。

常规的下垂控制算法中，ω*为一个预先设定的常数，代表理想电网基波角频率。下垂控制策略在具体实施中各有差异，本文中基于下垂控制的并网逆变器单相等效控制框图如图1所示。其中，电抗器与电容电流参考方向如图中箭头所示。本文中，通过虚线部分的采样电压计算输出端电压频率并实时传递给下垂控制器。

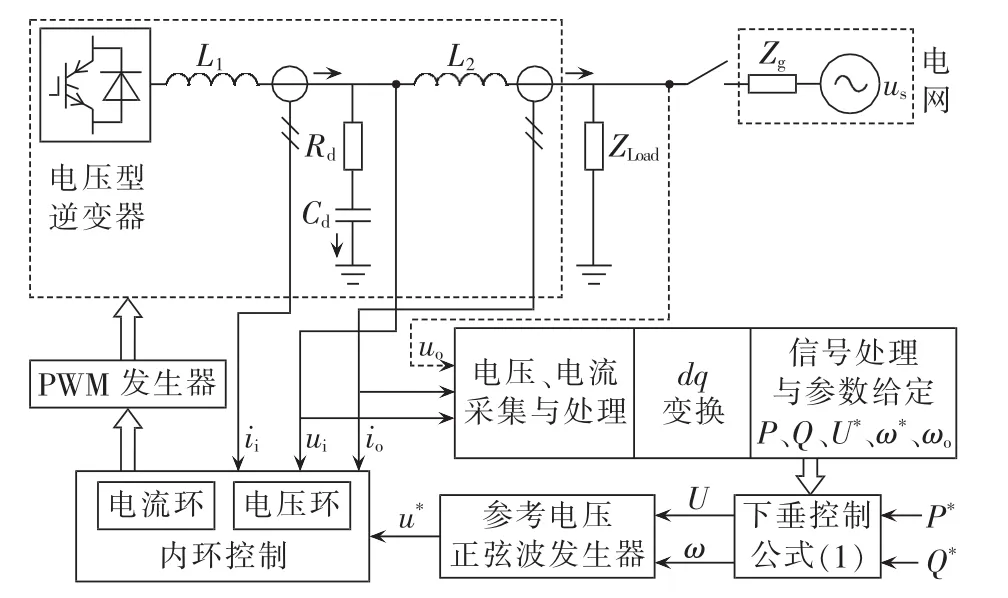
图1 并网逆变器下垂控制单相等效原理图Fig.1 Single-phase equivalent diagram of droop control for grid-connected converter

图中，us为电网电压；Zg为电网阻抗；uo为逆变器输出端电压；ωo为输出端电压角频率，由锁相环检测输出端三相电压得到；L1、L2和Cd组成逆变器输出LCL滤波器；Rd为阻尼电阻；ii为电抗器L1实际输出电流；io为逆变器输出电流。实际系统中，在L2和负载之间存在并网变压器，此处没有画出。以滤波电容点电压和逆变器输出电流计算得到逆变器输出有功和无功功率。

控制器采取电压外环、电流内环的双闭环结构。ZLoad为本地负载，通常用RLC并联支路来等效。正常并网运行和脱网运行时，并网逆变器均按照既定的角频率指令进行闭环工作。

2 孤岛检测方法及改进

2.1 孤岛检测方法

结合下垂控制器自身的特点，提出以下孤岛检测的方法。并网运行时令ω*等于ωo，其中ωo为并网逆变器输出角频率，受电网电压箝位，不会有较大波动。当非计划孤岛发生时，由于电网失电，逆变器输出端电压对ωo的箝位作用消失，此时逆变器输出频率会向某一方向偏移，即下垂控制器的基准频率发生偏移，当频率偏移超过预设值时，检测到孤岛现象发生；当要进行主动孤岛运行，即计划性孤岛运行时，下垂控制器不再采用ωo作为参考频率，而是将ω*置为一个固定值，来保证系统频率稳定。

本文提出的基于下垂控制环的孤岛检测方法，其原理可简单地用图2进行描述。图2为改进后的下垂控制有功-频率环，图中将参考电压的幅值进行了简化与忽略。有功功率P为负载阻抗ZLoad、输出电压幅值U和输出电压角频率ωo的函数。可以看出，与传统的闭环控制不同，其输入指令跟随输出变化，可以理解其为一个准正反馈系统。

图2 孤岛检测原理图Fig.2 Schematic diagram of islanding detection

假设系统可以实现无静差控制，即输出电压幅值为 U*，输出角频率，则逆变器输出的有功功率在电网失电前后之差可以表示为：

再结合图2，可以得到：

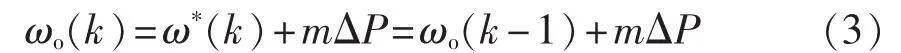
电网失电后有功变化ΔP会影响逆变器输出端电压的角频率。理想情况下，即系统可以实现无差控制与检测时，逆变器输出端电压的角频率ωo（k）=ωo（k-1）+mΔP，当有功变化为零时，系统输出电压角频率不会发生变化，即孤岛检测的盲区。

2.2 孤岛检测改进算法

从以上理论分析可见，当逆变器输出有功功率和本地负载消耗有功功率较接近时，发生孤岛现象时，逆变器输出频率的正反馈作用将会减弱，这将导致孤岛检测时间变长。为此，对提出的孤岛检测方法进行改进，加强其正反馈作用，进而缩短检测时间。

图3为改进的孤岛检测方法原理图。对图2中输出频率的反馈部分做了改进。

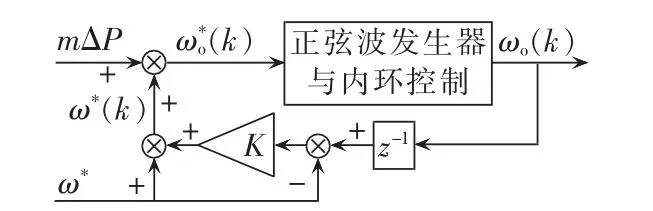
图3 孤岛检测改进方法Fig.3 Improved method of islanding detection

同样地，假定控制系统是理想的，可以得到电网失电后输出电压角频率表达式。可以看出，反馈强度系数K可以改变输出电压角频率的反馈强度。根据图3，得到输出电压角频率表达式如下：

根据式（4）分析可知，系数K大小不同，则检测的效果也会有所不同，具体如下：

a.K<0时，为负反馈，无法实现孤岛检测；

b.K=0时，退化为传统下垂控制策略；

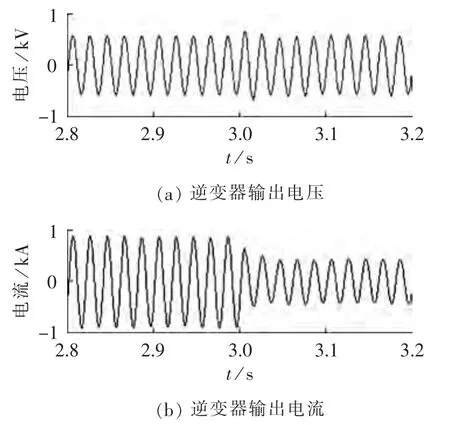
c.0

d.K=1时，退化为改进前的检测算法；

e.K>1时，加强了正反馈效果，可加速检测速度。

可以看出，K越大，其检测速度越快，但受到控制器响应速度的影响，检测时间不可能无限快。且过大的K值，会引起在正常并网运行时由于电网电压频率波动及频率检测的误差引入较大的偏差，不利于系统的稳定。因而需要根据具体情况设定K值。

另外，需要注意的是，实际电网不会保持某一频率恒定不变，因而可以在程序中每隔一段时间（如1 min）对图3和式（4）中的电网角频率ω*进行更新，当检测到的电网频率在电网标准正常范围之内时，用新值更新，而当超出正常范围时，保持上一个值不变；或者将逆变器输出端电压进行滑模平均，得到的结果在限定范围内时，设定为ω*值。

3 检测成功边界条件

根据式（4）可得：特殊地，当K=1时，即为检测方法改进前的传递函数。系统特征方程为：z=1。其不稳定的条件为：

因此，当满足K>1时才可以使系统输出电压频率不稳定，即可以提供检测到孤岛现象发生的条件。同样地，K值越大越不容易稳定，频率偏移也就越快，即所需的孤岛检测时间越短。

4 仿真验证

为了验证本文所提出的孤岛检测方法及其改进方案，在含有2台并网发电逆变器的系统中进行仿真验证，其中单台逆变器容量为720 kV·A，电网线电压有效值为690 V，基波频率fs=50 Hz，逆变器数量为2台，直流母线额定电压Ud=1100 V，LCL滤波器中 L1=300 μH、L2=180 μH、Cd=190 μF、Rd=0.1 Ω，下垂控制系数 m=3×10-6、n=1×10-4。

设定t=3 s时发生孤岛，负载阻抗为0.67Ω。图4为未采用任何孤岛检测算法时输出电压、电流波形。输出电压幅值在孤岛发生时会有暂态的微小波动；孤岛运行时输出电流发生变化，由负载特性决定。

2台逆变器采用控制算法相同，输出波形基本一致，因而只给出了其中一台逆变器相关波形。

图4 未采用孤岛检测方法时相关波形Fig.4 Waveforms of inverter without islanding detection

图5为未采用孤岛检测方法时输出电压的频率。频率的静态工作点发生偏移，但仍未超过相关标准，且能够稳定在某一频率点附近。这是传统下垂控制算法的优势，即能够实现并网到孤岛的平稳切换，然而也正是如此，使其不能对孤岛现象做出检测。

图5 未采用孤岛检测方法时逆变器输出电压频率Fig.5 Voltage frequency of inverter without islanding detection

加入孤岛检测算法，在不同负载特性下进行仿真验证。

图6为负载阻抗为0.67 Ω，即轻载时，不同反馈强度系数K下，逆变器的输出电压频率图。可见，在孤岛发生之前，逆变器输出频率保持在电网频率；孤岛发生后，随着反馈强度的增大，即K值的增大，频率偏移速度变快，相应地，在设定相同频率阈值的情况下所需要的孤岛检测时间越短。特别地，图中K=0.5时，无法检测到孤岛现象，这是由于其不满足式（7）所给出的检测成功的边界条件所造成的。

图6 轻载时不同系数K下逆变器输出电压频率Fig.6 Voltage frequency of inverter with light load for different values of coefficient K

逆变器输出电压、电流与未采用孤岛检测算法时基本一致，此处不再给出。

将阻性负载阻抗改为0.29 Ω，此时负载消耗有功大于逆变器额定输出有功功率，逆变器输出电压频率如图7所示。可以看出，此时频率偏移方向与轻载时正好相反。

将阻性负载阻抗改为0.33 Ω，此时逆变器输出功率与负载消耗功率相匹配，其他条件不变，仿真结果如图8所示。可以看出，相对于负载功率较大的情况，当功率匹配时，在K值较小时（图中K=1和K=0.5时），频率偏移速度显著减慢；而采用改进策略时，即选取较大的K值，频率偏移速度变化不大。

图7 逆变器额定有功功率小于负载消耗时输出电压频率Fig.7 Output voltage frequency when rated inverter power is smaller than load

图8 逆变器功率和负载功率匹配时逆变器电压频率Fig.8 Voltage frequency when inverter power matches load power

采用RLC负载进行仿真，设定负载谐振频率点为 f0=50 Hz（L=500 μH，C=20.26 mF），反馈强度系数K=5不变。图9为系统在不同的负载品质因数（品质因数情况下的仿真结果。可以看出，品质因数的变化会影响该算法的检测速度，但即使Q>2.5，也可以成功实现孤岛检测。

图9 不同负载品质因数时逆变器电压频率Fig.9 Voltage frequency for different load quality factors

在发生孤岛现象和系统检测到孤岛的时间段内，由于输出频率的偏移，检测算法会对逆变器下垂控制的控制效果产生一定影响，但并不影响稳态运行。需要特别说明的是，当系统需要进行主动孤岛运行时，只需在程序检测到孤岛现象发生后将反馈强度系数K置为0，控制器即转化为传统的下垂控制策略，可以实现平稳过渡到孤岛运行。这样本文所提出的控制方案就可以兼顾系统的计划孤岛运行和非计划孤岛现象快速检测，大幅提高系统的灵活度和可靠性。

5 结论

针对现有主动孤岛检测算法普遍会降低并网运行电能质量的问题，本文提出了一种基于下垂控制的孤岛检测方法及其改进策略。理论分析和仿真结果证明，其在稳态运行时不会对电能质量造成影响。依据给出的检测成功的边界条件，合理设定反馈强度，可以在各种负载条件下无盲区地实现孤岛检测并改变检测所需时间。当局部电网存在多个分布式能源系统时，只要均采用此孤岛检测手段，不同系统检测效果不会相互影响。