三相短路故障时小容量发电机出口断路器瞬态恢复电压

刘渝根，米宏伟

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

近年来，随着新能源技术的蓬勃发展，小容量（≤30 MW）发电机组也得到了广泛的应用。学者已论证了大容量发电机组出口装设发电机断路器（GCB）的必要性［1-5］，但是对于小容量的发电机组出口是否应装设发电机断路器并没有进行深入的研究。

同时由于技术和材料的改进，普通配电型断路器逐渐可适应开断条件更为苛刻的场合［6-7］。因此对于设计人员而言，一般采用改进的配电型断路器安装在发电机出口处。但是改进的配电型断路器在设计时仅考虑了断路器开断直流分量的能力，而没有考虑断路器开断后的瞬态恢复电压。而断路器的瞬态恢复电压（TRV）上升率过大会影响断路器的开断能力，从而导致断路器发生故障［8-10］。

在发电机回路中，发电机出口断路器开断时TRV上升率较高［11-14］。 GB /T 14824—2008《高压交流发电机断路器》规定：对于额定电压为12 kV的断路器，由系统源提供短路电流时，TRV上升率的标准值为3.5 kV/μs；由发电机源提供短路电流时，TRV 上升率的标准值为1.6 kV/μs。普通配电型断路器仅能满足TRV上升率为0.34 kV/μs的情况，而不适合安装在TRV上升率较高的发电机回路中。由于制造工艺和所采用的材料的不同，发电机断路器和普通配电型断路器的价格相差很大：每台发电机断路器价格为70万元，而每台配电型断路器价格仅为12万元。

从技术的角度看，发电机出口安装发电机断路器更能确保系统的安全可靠；从经济的角度看，发电机出口安装配电型断路器更为合理。因此本文从TRV上升率的角度出发，对小容量（≤30 MW）发电机出口断路器的TRV进行仿真研究，确定在何种条件下配电型断路器可以替代发电机断路器安装在发电机出口处。同时为满足实际工程的需要，笔者还在仿真研究的基础上推导了用于计算发电机出口断路器TRV大小的公式，并验证了该公式的正确性。

1 仿真模型的建立

1.1 断路器模型

本文用非线性电阻来模拟发电机断路器的动态状况：通过搭建控制系统控制非线性电阻值，来模拟断路器处于合闸、稳态燃弧、熄弧断开时的状态。

断路器处于合闸状态时，其主回路电阻很小［15］。上海通用电气开关有限公司提供的断路器产品说明书中表明，不同型号的断路器主回路电阻值在40～60 μΩ之间。为不失一般性，本文取断路器主回路电阻值为 50 μΩ。

断路器在操动机构的作用下，动静触头开始分离，此时两触头间产生稳态燃烧的电弧。文献［16］表明稳态燃弧阶段弧阻基本为恒定值，其大小与回路的振荡频率有关，阻值基本在0.5～5.0 Ω 之间。 为不失一般性，本文取稳态燃弧阶段弧阻为2 Ω。

在电弧电流过零瞬间，外界电路向电弧提供的能量小于电弧散失的能量，从而进入熄弧阶段［17-20］。这个过程可以用Mayr-Schwarz模型描述：

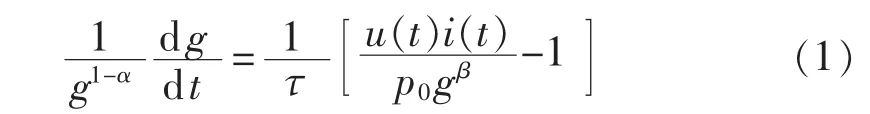
其中，u（t）为电弧电压（V）；i（t）为电弧电流（A）；g 为电弧电导（S）；p0为电弧散热功率（W）；τ为时间常数（s）。根据典型的12 kV断路器开断实验所获得的零区波形，利用最小函数法可计算出电弧模型中各参数的取值：α=0.14，β=0.30，τ=10 μs，p0=120 kW。

由式（1）可知，在熄弧阶段电弧电阻是非线性的。因此在仿真过程中，断路器可以用一非线性电阻来等效代替，对该非线性电阻的控制过程如图1所示。

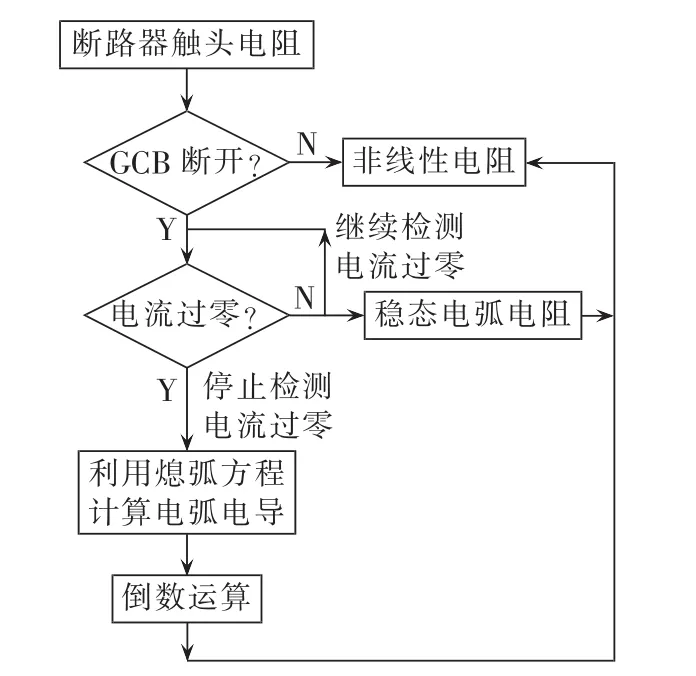
图1 非线性电阻控制流程图Fig.1 Flowchart of nonlinear resistor control

1.2 同步发电机模型

在本文的仿真分析中，发电机采用的是PSCAD模型库中的同步发电机模型，如图2所示。

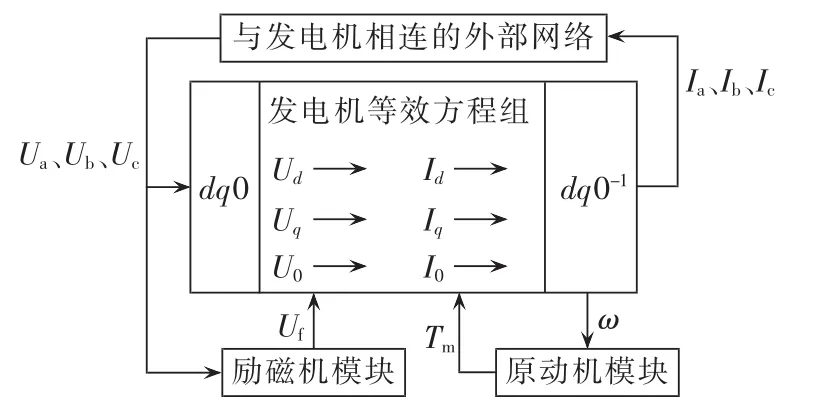
图2 发电机模型图Fig.2 Schematic diagram of generator model

该模型用诺顿电流源等效代替同步发电机，利用发电机的额定电压实时计算三相电流，并注入外部网络。为计算方便，该模型首先把相坐标系下的三相电压Ua、Ub、Uc转换成dq0坐标系下的dq轴绕组端电压Ud、Uq、U0，并通过dq轴等效电路及状态空间方程组，计算出 dq0 坐标系下的电流 Id、Iq、I0，并再次转换成相坐标系下的三相电流Ia、Ib、Ic，进而注入外部网络。

这个模型充分考虑了定子绕组、励磁绕组及阻尼绕组的暂态过程，适用于分析发电机机端或变压器外部故障及故障切除后的暂态过程。仿真模型中，不同容量的发电机参数如表1所示。表中，Rs为发电机定子绕组的直流电阻；Xd为直轴电抗标幺值；X′d为直轴暂态电抗标幺值；X″d为直轴次暂态电抗标幺值。

1.3 系统模型

仿真模型是按照“同步发电机-断路器-变压器-系统源”的接线形式建立的。

表1 不同容量发电机参数Table 1 Generator parameters for different capacities

图3中，电缆型号为ZR-YJV22-12/20 kV-3×240mm2；变压器为△-Y 接线方式，变比为（121±8×1.25%）kV/10.5 kV；110 kV系统源用一个理想电压源串电感进行等效，该电感的计算如式（2）所示。

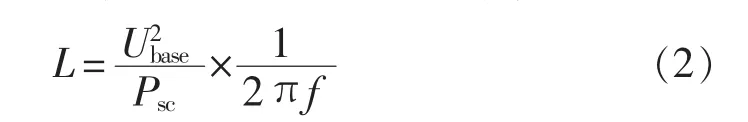
其中，Ubase为系统源的基准电压（kV）；Psc为系统源的短路容量（MW）；f为电源频率（Hz）。

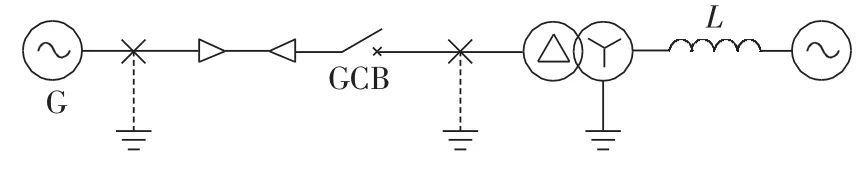
图3 仿真模型图Fig.3 Schematic diagram of simulation model

通过比较发电机回路中发生单相接地故障、两相短路故障、三相短路故障等不同故障情况下的计算结果，发现系统中发生三相短路故障时，发电机出口断路器开断条件最为恶劣。因此本文主要阐述系统中发生发电机出线端三相短路故障、变压器低压侧出线端三相短路故障这2种故障情况下，发电机断路器的TRV，其中故障位置如图3中虚线接地部分所示。

仿真模型中设定系统在0.237 s发生三相短路故障，在继电保护及断路器操动机构动作后，在0.302 s断路器两触头间出现电弧。

2 发电机出线端三相短路故障时断路器TRV仿真分析

2.1 12 MW发电机断路器TRV仿真分析

以12 MW发电机为例，当发生发电机出线端三相短路故障时，三相短路电流及出现在断路器断口间的TRV波形分别如图4和图5所示。

图4 三相短路电流波形Fig.4 Waveform of three-phase short circuit current

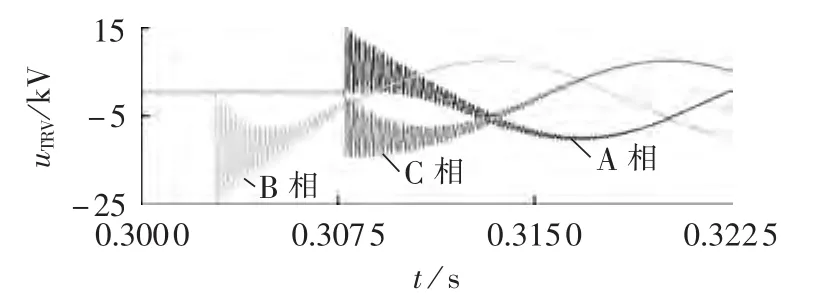
图5 断路器断口间的TRV波形Fig.5 Waveforms of TRV between open contacts of circuit breaker

图4表明：三相短路电流的最大值为16.37 kA，无电流延迟过零点状况。通过对短路电流进行傅里叶变换可知，短路电流的交流分量有效值为7.64 kA，直流分量百分数为23%。在本文的研究中，对于不同容量（≤30 MW）的发电机回路，在发生不同短路故障后，短路电流的交流分量有效值最大为26.81 kA、直流分量百分数最大为29%。而普通配电型断路器能够开断40 kA、直流分量百分数为35%的短路电流，但其TRV上升率参数仅为0.34 kV/μs。因此本文在对发电机出口断路器的选型中，对断路器开断短路电流的能力不再赘叙，而着重从TRV上升率的角度出发确定在何种条件下普通配电型断路器可以替代发电机断路器。

由于B相断路器电流最先过零使其电弧熄灭，故B相是首开相，其断口间最先出现TRV；A、C两相断路器电弧电流同时过零、同时开断，其断口间同时出现TRV，且出现的时间滞后B相5 ms。三相断路器断口间的TRV经过5～7 ms的衰减振荡后，过渡到幅值为7.87 kV的工频恢复电压。改变故障发生的时间，使A相、C相分别作为首开相，得到的仿真结果与上述情况类似。

对三相断路器断口间的TRV波形进行分析计算后，可得到如表2所示的计算结果，表中Uc为TRV的峰值电压；t3为TRV的参考时间；Uc/t3为TRV的上升率；feq为TRV的等值频率。由表2可见，B相断路器TRV波形的峰值电压及上升率最大，A、C两相断路器TRV波形中的峰值电压及上升率相接近且略低于首开相断路器TRV波形中的峰值电压及上升率；首开相断路器TRV波形的等值频率要低于随后断开的A、C两相断路器TRV波形的等值频率。这是因为当B相断路器开断后，电路中的拓扑结构已发生了改变，从而导致首开相和随后开断的两相断路器TRV波形在峰值电压、参考时间、上升率、等值频率等参数上的不同。

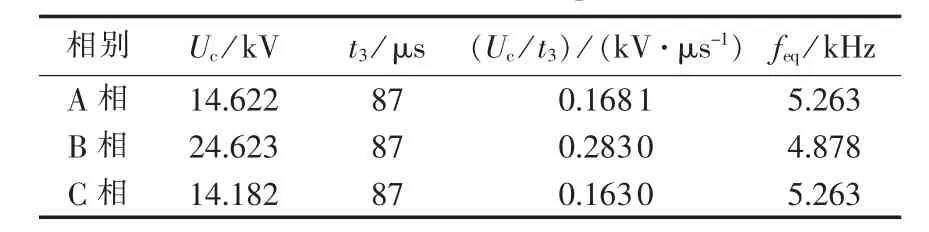
表2 三相断路器瞬态恢复电压计算结果Table 2 Calculative TRV of three-phase circuit breaker

表2 中的计算结果表明：三相断路器TRV上升率的最大值为 0.283 0 kV /μs（首开相），要低于GB 1984—2003《高压交流断路器》对额定电压为12 kV的配电型交流断路器TRV上升率的规定值0.34 kV/μs，更低于 GB/T14824—2008《高压交流发电机断路器》对由系统源提供的、额定电压为12 kV的发电机断路器TRV上升率的规定值3.5 kV/μs。这就表明在“同步发电机-断路器-变压器-系统源”的主接线形式下，当发生发电机出线端三相短路故障后，使用配电型断路器能够满足GB1984—2003《高压交流断路器》对断路器TRV的要求。即在这种情况下，普通配电型断路器可以替代发电机断路器安装在发电机出口处。

2.2 12～30 MW小容量发电机断路器TRV仿真分析

从以上分析可知，首开相断路器TRV上升率最大，最难开断。因此本节在对12～30 MW的小容量发电机断路器TRV的仿真研究中，均以首开相为例进行说明。

当发电机出线端发生三相短路故障时，在发电机容量为 15 MW、18 MW、20 MW、22 MW、30 MW 的情况下，分别对发电机断路器TRV进行仿真分析，并对TRV波形参数进行计算，计算结果如表3所示，表中S为发电机容量。

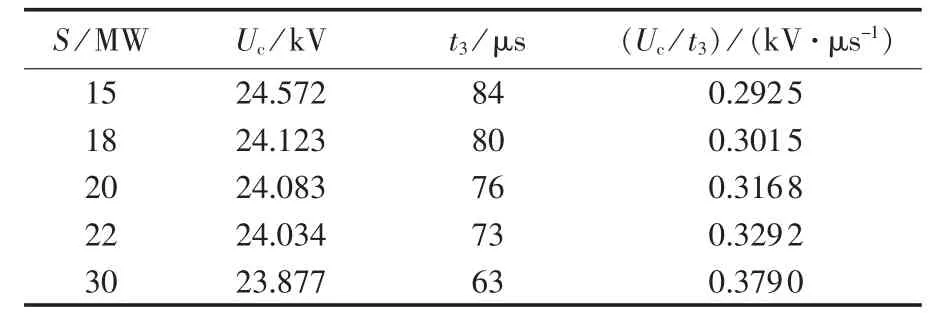
表3 不同容量的发电机断路器TRV计算结果Table 3 Calculative TRV of generator circuit breaker for different capacities

表3表明：当发电机出线端发生三相短路故障时，随着发电机容量的增大，首开相断路器断口间TRV参考时间急剧减小，TRV上升率随之增大。利用编制的MATLAB程序，绘制出首开相断路器TRV上升率随发电机容量变化的曲线，如图6所示。

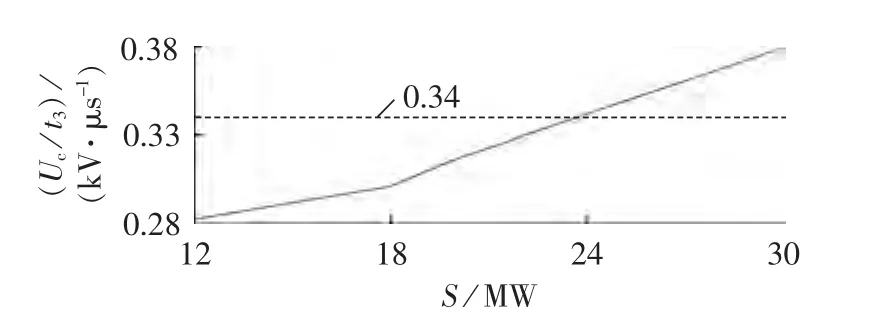
图6 TRV上升率与发电机容量之间的关系曲线Fig.6 Relationship curve between TRV rising rate and generator capacity

图6表明：随着发电机容量的增大，TRV上升率也随之增大，且发电机容量为12～18 MW时TRV上升率增大的速率要低于发电机容量为18～30 MW时的TRV上升率增大的速率；当发电机容量在24 MW以下时，TRV上升率均未超过0.34 kV/μs。即在24 MW以下的小容量发电机中，当发生发电机出线端三相短路故障后，普通配电型断路器可以替代发电机断路器安装在发电机出口处。当发电机容量在24 MW以上时，TRV上升率已超过0.34 kV/μs。即在24MW以上的小容量发电机中，当发生发电机出线端三相短路故障后，普通配电型断路器不可以替代发电机断路器安装在发电机出口处。

2.3 TRV手算公式

在实际工程中，设计人员更倾向于利用简便的公式快速计算出TRV的大小。因此为推导出首开相断路器TRV的计算公式，本文把图3所示的三相电路等效为单相电路（首开相断路器断开、其余两相断路器闭合），如图7所示。图中 Ueq、Req、Leq、Ceq分别为系统等效电源、电阻、电感和电容。

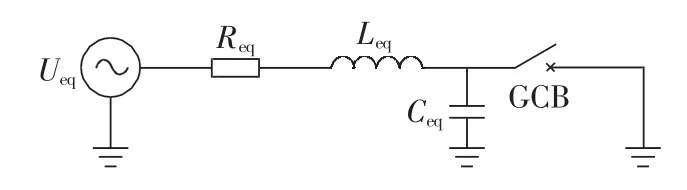
图7 断路器TRV的单相计算等值电路Fig.7 Single-phase equivalent circuit of circuit breaker for TRV calculation

当等效电路中元件参数满足式（3）所示的数学条件时，可推导出TRV的数学表达式，如式（4）所示。

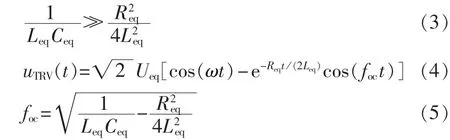
其中，uTRV（t）为 TRV 瞬时值；ω 为电源频率；foc为由电路参数确定的振荡曲线的频率。

根据式（3）所示的等效电路中各元件参数满足的数学条件，可求取TRV的峰值电压Uc及参考时间 t3分别如式（6）、式（7）所示。

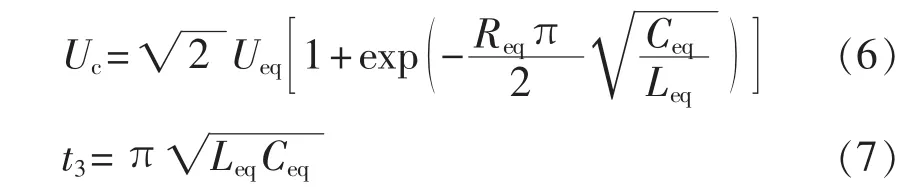
根据仿真结果，逐步修正图6中各等效参数的取值公式，如式（8）所示。

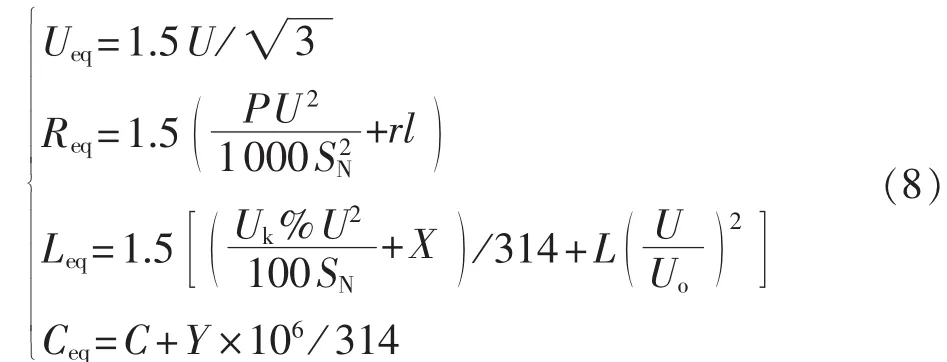
其中，U为变压器低压侧的额定电压（kV）；SN为变压器的额定容量（MV·A）；P为变压器的铜耗（kW）；Uk%为变压器的短路电压百分数；C为变压器低压绕组对地电容（μF）；L为系统源等效短路电感（H）；Uo为系统源电压（kV）；r为单位长度电缆的直流电阻（Ω/km）；l为电缆长度（km）；X 为电缆电抗（Ω）；Y为电缆容纳（S）；Ueq、Req、Leq、Ceq的单位分别为 kV、Ω、H、μF。

利用式（4）—（8），编制 MATLAB 程序，绘制出当12 MW发电机出线端发生三相短路故障时，首开相断路器的TRV波形，如图8所示。

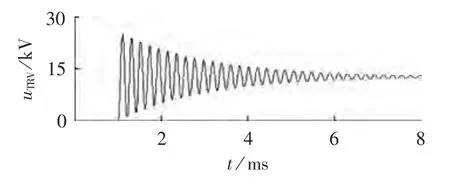
图8 MATLAB程序绘制的断路器TRV波形曲线Fig.8 Circuit breaker TRV waveform drawn by MATLAB program

程序运行结果为：TRV峰值电压为25.0545 kV，参考时间为 91 μs，TRV 上升率为 0.2753 kV/μs，等值频率为4.8169 kHz。将该结果及图8波形同图5中B相TRV波形及表2中B相断路器TRV计算数据相比较后可以看出，二者之间误差不大。即在实际工程中，可用式（4）—（8）来计算发电机出口断路器的TRV。当发电机容量为15 MW、18 MW、20 MW、22 MW、30 MW 时，用式（4）—（8）计算出的结果均与仿真结果吻合，进一步验证了式（4）—（8）TRV计算公式的正确性。

3 变压器低压侧出线端三相短路故障时断路器TRV仿真分析

3.1 12 MW发电机断路器TRV仿真分析

以12 MW发电机为例，当变压器低压侧出线端发生三相短路故障时，出现在断路器断口间的TRV波形如图9所示。

图9 断路器断口间的TRV波形Fig.9 Waveforms of TRV between open contacts of circuit breaker

对三相断路器断口间的TRV波形进行分析计算后，可得到如表4所示的计算结果。由表4可见：B相断路器TRV波形的峰值电压及上升率均最大，同时开断的A、C两相断路器TRV波形的峰值电压及上升率相接近且略低于首开相断路器TRV波形的峰值电压及上升率；首开相断路器TRV波形的等值频率要低于随后断开的A、C两相断路器TRV波形的等值频率。这是因为当B相断路器开断后，电路中的拓扑结构已改变，从而导致首开相和随后开断的两相断路器TRV波形的峰值电压、参考时间、上升率、等值频率等参数不相同。

表4 三相断路器瞬态恢复电压计算结果Table 4 Calculative TRV of three-phase circuit breaker

同样B相断路器电流最先过零使其电弧熄灭，B相是首开相，其断口间最先出现TRV；A、C两相断路器电弧电流同时过零同时开断，其断口间同时出现TRV，且出现的时间滞后B相5 ms。三相断路器断口间的 TRV经过 0.68 ms的衰减振荡后，过渡到幅值为7.21 kV的工频恢复电压。改变故障发生的时间，使A相、C相分别作为首开相，得到的仿真结果与上述情况类似。

表4 的计算结果表明：三相断路器TRV上升率最大值为 0.176kV/μs（首开相），低于 GB1984—2003《高压交流断路器》对额定电压为12 kV的普通配电型交流断路器TRV上升率的规定值0.34 kV/μs，更低于GB/T14824—2008《高压交流发电机断路器》对由发电机源提供的、额定电压为12 kV的发电机断路器TRV上升率的规定值1.6 kV/μs。这就表明在“同步发电机-断路器-变压器-系统源”的主接线形式下，当发生主变压器低压侧出线端三相短路故障后，使用普通配电型断路器能够满足GB1984—2003《高压交流断路器》对断路器瞬态恢复电压的要求。即在这种情况下，普通配电型断路器可以替代发电机断路器安装在发电机出口处。

3.2 12～30 MW小容量发电机断路器TRV的仿真分析

同样对于12～30 MW小容量发电机断路器而言，首开相断路器TRV上升率最大，最难断开。因此本节在对12～30 MW小容量发电机断路器TRV的仿真研究中，均以首开相为例进行说明。

当变压器低压侧出线端发生三相短路故障时，在发电机容量为15 MW、18 MW、20 MW、22 MW、30 MW的情况下，分别对发电机断路器TRV进行仿真分析，并对TRV波形参数进行计算，计算结果如表5所示。

表5表明：随着发电机容量的增大，首开相断路器断口间TRV参考时间逐渐减小，TRV上升率逐渐增大。这是因为不同容量的发电机，同步电抗、暂态电抗、次暂态电抗不同，从而导致TRV上升率的不同。利用编制的MATLAB程序，绘制出首开相断路器TRV上升率随发电机容量变化的曲线，见图10。

表5 不同容量的发电机的断路器瞬态恢复电压计算结果Table 5 Calculative TRV of generator circuit breaker for different capacities

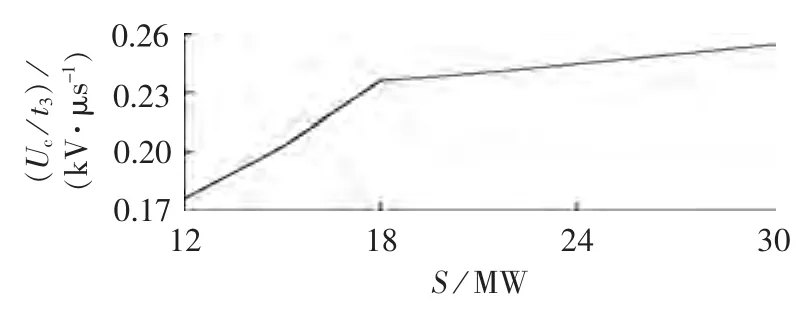
图10 TRV上升率与发电机容量之间的关系曲线Fig.10 Relationship curve between TRV rising rate and generator capacity

图10表明：随着发电机容量的增大，TRV上升率也随之增大，且发电机容量为12～18 MW时TRV上升率增大的速率要高于发电机容量为18～30 MW时的TRV上升率增大的速率。当发电机容量为12～30 MW 时，TRV 上升率最大值为 0.2542 kV/μs，没有超过 0.34 kV/μs，即在 12～30 MW 的小容量发电机中，当发生变压器低压侧出线端三相短路故障后，普通配电型断路器可以替代发电机断路器安装在发电机出口处。

3.3 TRV 手算公式

同样为满足实际工程的需要，本文也推导了在变压器低压侧出线端发生三相短路故障的情况下，用于计算首开相断路器TRV的公式。等效电路及相关数学公式分别如 2.3节中的图7及式（3）—（7）所示。

根据仿真结果，逐步修正图7中各等效参数的取值公式，如式（9）所示。

其中，U为发电机的额定电压（kV）；X′d为发电机的暂态电抗标幺值；S为发电机的额定容量（MV·A）；R为发电机定子绕组电阻（Ω）；C为发电机绕组对地电容（μF）；r为单位长度电缆的直流电阻（Ω/km）；l为电缆长度（km）；X为电缆电抗（Ω）；Y为电缆容纳（S）；Ueq、Req、Leq、Ceq的单位分别为 kV、Ω、H、μF。

利用式（3）—（7）及式（9），编制 MATLAB 程序，绘制出当发电机容量为12 MW且变压器低压侧出线端发生三相短路故障时，首开相断路器的TRV波形，如图11所示。

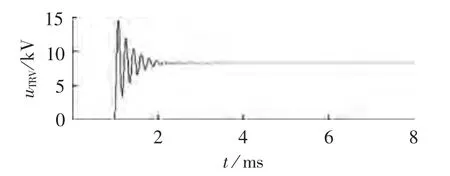
图11 MATLAB程序绘制的断路器TRV波形曲线Fig.11 Circuit breaker TRV waveform drawn by MATLAB program

程序运行结果为：TRV峰值电压为14.012 kV，参考时间为 79 μs，TRV 上升率为 0.1773 kV/μs，等值频率为5.58 kHz。将该结果及图11中波形和图9中B相TRV波形及表4中B相断路器TRV计算数据相比较后可以看出，二者之间误差不大，即在实际工程中，可以利用式（3）—（7）、（9）计算发电机断路器的TRV。当发电机容量为15 MW、18 MW、20 MW、22 MW、30 MW 时，利用式（3）—（7）、（9）计算出来的结果均与仿真结果相吻合，进一步验证了式（3）—（7）、（9）TRV 计算公式的正确性。

由式（8）、（9）及大量的仿真计算可知，系统源的短路容量、变压器的阻抗等参数对发电机断路器的TRV值有一定的影响。但大量安装小容量发电机组的新能源发电厂一般接于110 kV的交流系统，此时系统源的短路容量、变压器的阻抗等参数可以看为一个定值，故其对发电机断路器的TRV影响不大。

一个工频周期内不同的短路时刻对发电机断路器的TRV也有一定的影响。通过大量的仿真计算可知，当系统中发生三相短路故障时，系统电源电压恰好处于峰值，此时发电机断路器的TRV最大。由于系统发生短路的时刻具有随机性，因此本文选取有代表性的时刻0.237 s（此时系统电源电压处于峰值）作为系统发生三相短路故障的时刻。

4 结论

本文利用PSCAD/EMTDC电磁暂态仿真软件，计算了在发电机回路中发生断路器开断条件最恶劣的2种故障情况时，发电机断路器的TRV，并从TRV上升率的角度出发确定在何种条件下配电型断路器可以替代发电机断路器安装在发电机出口处。本文得到结论如下。

a.当发电机出线端发生三相短路故障时，首开相断路器TRV上升率最大，且TRV上升率随发电机容量的增加而增大；当发电机容量为12～24 MW时，TRV上升率均未超过0.34 kV/μs，普通配电型断路器可以替代发电机断路器安装在发电机出口处。当发电机容量为24～30 MW时，TRV上升率已经超过0.34 kV/μs，普通配电型断路器不能替代发电机断路器安装在发电机出口处。

b.当变压器低压侧出线端发生三相短路故障时，首开相断路器TRV上升率最大，并且TRV上升率随着发电机容量的增加而增大；当发电机容量为 12～30 MW 时，TRV 上升率均未超过 0.34 kV/μs，普通配电型断路器可以替代发电机断路器安装在发电机出口处。

c.为满足实际工程的需要，将实际三相电路等效为单相电路，推导出发电机断路器TRV的计算公式及等效电路中各参数的取值方法，并通过多次仿真计算验证了该公式的正确性。