电动汽车规模化接入配电网的充电优化
杨秀菊,白晓清,李佩杰,韦 化
(广西大学 广西电力系统最优化与节能技术重点实验室,广西 南宁 530004)
0 引言
在国内外,电动汽车 EVs(Electric Vehicles)将成为实现节能减排的必然选择。调查表明[1],90%的充电行为是发生在停车场、家庭车库等固定场所的慢充方式,未来这也将是我国家用EVs规模化入网的方式。配电网作为其接入端,直接与用户相连,是分配电能的主要环节,约95%的停电事故源于此,且有功损耗约占整个输配电系统的50%[2]。EVs大规模接入必将对配电网的安全、经济运行带来巨大的挑战。
当EVs作为负荷通过智能设备接入配电网时,该负荷具有可控性。电网可以通过实时信息互动,对其进行负荷调度,使其作为发电调度的补充,优化系统运行。但该负荷也具有随机性和不均衡性,无序充电可能导致配网节点电压恶化,影响用电设备的正常启动和运行,甚至可导致配变严重过载、保护动作。虽然配变扩容或新增可以满足EVs的充电需求,但会造成资源的不合理利用。此外,EVs随机充电还造成日负荷峰谷差的恶化,对电网的安全稳定运行带来很大的隐患。
目前已有不少EVs入网的研究成果。文献[3]对充电负荷进行了详细建模,采用蒙特卡洛模拟方法模拟EVs充电行为,计算各时段的充电需求。文献[4]将充电过程视为由低荷电状态(SOC)向高荷电状态扩散的动态过程,提出基于扩散理论的EVs充电负荷模型。文献[5-7]将表征充电特性的分布函数离散化,求取充电功率的期望值。文献[8]针对2个实际的配网区域进行研究,表明EVs的随机充电会大幅增加有功网损,指出通过优化充电降低网损的必要性。文献[6-7]以负荷波动最小为目标优化大型车辆集聚体的各时段充电功率,但研究未涉及网架结构。文献[9-10]的研究是在低压配电网层次,建立充电优化模型以优化每台车辆的充电行为。文献[11]考虑潮流及电压安全约束,建立了中压配网的充电优化模型,但未涉及线路重载、配变过载等问题。在模型的求解方法上,文献[6]的模型调用MATLAB中的SQP工具箱求解,文献[10]将模型转化为线性规划进行求解,文献[11]将模型转化为凸二次规划问题求解。
本文计及充电起始时间及充电时长的随机性,建立充电负荷的概率模型以期求取充电需求,使模型更符合实际情况,旨在寻找一种简便、有效的方法估计充电需求;以最小化有功网损为目标函数,在满足充电需求的条件下,计及潮流、节点电压、线路和配变容量约束,建立了配电网的充电优化问题模型,采用原-对偶内点法求解,优化以配变台区为单位的EVs集聚体的充电行为;以3个配电系统为算例,验证所提模型及方法的合理性和有效性。
文中所建模型基于以下几点假设:
a.依托智能电网技术,已经注册为可调度的EVs与电网进行实时的信息互动,能够响应电网调度的需求;
b.EVs行程前电池均到达满电量,充电过程中,充电速率连续可调至充满;
c.以城市中压配电网为研究对象,三相供电平衡,可简化计算,仅对单相配线进行研究。
1 EVs的充电负荷模型
文献[5]采用每小时充电功率的均值研究电动汽车在不同渗透率下对系统日负荷曲线的影响。文献[12]根据求取的EVs每小时消耗电能的期望值,乘以行驶的电动汽车数量得到每个调度时段电动汽车的总的电能需求。文献[13]采用蒙特卡洛模拟法和计算充电功率期望值的概率建模法计算同一情境下的充电负荷,对比了2种方法的求解精度和计算时间,表明两者计算精度大体一致,误差较小,但是前者计算耗时3312.9998 s,后者仅需0.0487 s,后者大幅提高了计算效率。
为方便研究,以Nissan Altra的锂离子电池为例,假设EVs均为该类型电池,容量为32.78 kW·h,充电时长为5 h,平均充电功率约为6.5 kW[14]。
本文针对面向居民生活负荷供电的城市配电网,EVs的充电方式为慢充,地点基本固定。行驶路程及行程结束时刻的概率密度函数PDF(Probability Distribution Function)见文献[3]的式(1)、(2)。 假设随机盲充状态下,行程结束后即开始充电,充电起始时间的PDF即行程结束时刻的PDF。
假设电池耗电量随行驶路程线性变化,则所需充电时长的表达式如下:

其中,k为充电时长;Tc为电池荷电状态从0至充满所需总时长;d为日行驶路程,其服从对数正态分布[3],其均值和标准差分别为 μ、σ;dmax为最大行驶路程。可得车辆行驶1 d后所需充电时长的PDF表达式为:
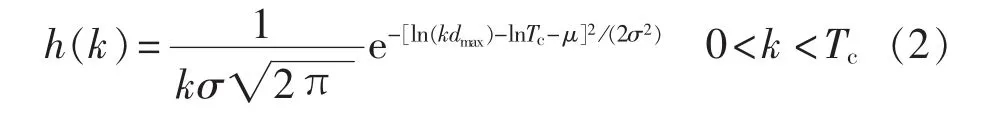
为预测各时段充电负荷,将充电起始时间及充电时长的连续分布函数以1 h为单位离散化[15]。
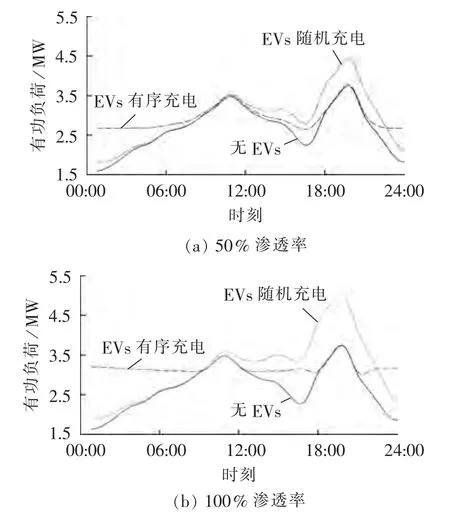
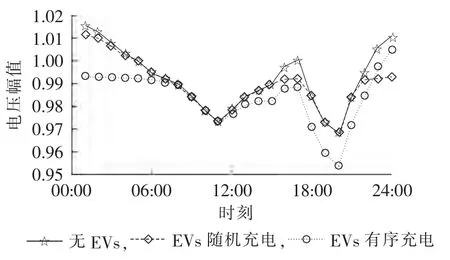
当0 其中,fp(x)为 x 时段开始充电的概率;hp(k)为充电时长为k的概率。将充电起始时刻及充电时长的连续分布函数分别以 1 h 为单位离散化[15]可得到 fp(x)及hp(k)。假设EVs电池的充电特性相同,第i个集聚体的可调度车辆数目为NEi,各辆EV在t时刻的充电功率用 PEV1(t)、PEV2(t)、…、PEVNEi(t)表示,为 NEi个独立同分布的随机变量[5,12-13]。 则 t时刻 EVs的期望充电功率为: 其中,Paver=6.5 kW为平均充电功率。 配电网的降损一直是备受关注的问题,在保证系统安全运行的前提下,通过优化调度各时段EVs充电负荷,降低系统有功网损,提高运行经济性。 其中,SL为所有支路集合;T、Δt分别为研究周期和研究时间段间隔;Ui,t、Uj,t分别为 t时刻支路的首、末端电压幅值;δij,t= δi,t- δj,t为 t时刻支路的首、末端电压相角差;Gij为互导纳的实部。 (1)等式约束条件。 a.节点功率平衡方程: 其中,jєi表示与节点 i存在相连支路的节点 j;iєSB,SB为所有节点的集合;PGi,t、QRi,t分别为 t时刻电源点的有功、无功出力;PLi,t、QLi,t分别为 t时刻负荷节点 i的有功和无功功率;Gij、Bij分别为互导纳的实部和虚部;PEi,t为 t时刻节点 i的充电功率,QEi,t为充电过程中引入的无功功率,功率因数为0.95。 b.充电能量平衡方程。 优化后的各时段充电功率之和等于该节点EVs集聚体的日充电需求。 其中,η=0.92 为充电效率[16]。 (2)不等式约束条件。 a.节点电压满足电压质量要求。 b.为避免配变长期过载运行,新增负荷需保证各节点负荷不超过其配变允许接入的最大有功负荷。 c.为避免线路过载,馈线潮流应满足线路容量约束。 d.由于各负荷节点的EVs数量有限,优化后任意时段的充电功率不得超过该节点的所有EVs同时充电的负荷,且考虑充电过程中的能量损失,在电网送能和EVs受能之间存在一个充电能量转换效率。 e.充电功率的动态爬升约束。由于电池技术本身的要求以及考虑充电对电网的冲击性,不希望各时段间充电功率大范围波动,波动范围设为最大充电功率的20%。 其中,带“-”、“_”变量为变量约束的上、下限值;Si为节点i配变的视在功率;cos ψ为功率因数,取值0.8;ρ 为配电变压器效率,取值 0.95;Pij,t为流过支路(i,j)的有功潮流;NEi为集中在配电节点i处的EVs集聚体的可调度车辆数量 随着配电网智能化的进一步发展,分区下达调度指令有望实现,将配电网的入网EVs进行分区管理,各代理商负责监控其管辖区内的可调度车辆,如图1所示。在充电接口安装智能充电装置,车辆可方便地响应调度指令,并采用一定的激励政策引导用户积极参与互动。以Agent 2为例,说明EVs充电优化调度的思想:Agent 2负责管辖监控7—18号配变的入网EVs的充电,每台配变下EVs集聚体优化后的各时段充电负荷从模型中已求出;借鉴文献[17]中的分布式优化控制策略,代理商监控这些配变下每台车辆的充电时间及充电功率,使其满足各个配变节点的各时段充电负荷。EVs用户响应代理商的调度控制命令。 图1 IEEE 33节点系统的网络拓扑图Fig.1 Topology of IEEE 33-bus system 模型考虑了不同时间断面的耦合性,属于动态潮流优化问题,求解规模大,复杂程度高,对算法的要求也愈高。基于扰动KKT(Karush-Kuhn-Tucker)条件的原-对偶内点法[18]具有较强的鲁棒性,计算速度快,对初值不敏感,且迭代次数与系统规模无关,在求解电力系统优化问题中已得到广泛应用。算法求解思路如下:引入松弛变量将不等式约束转化为等式约束,利用拉格朗日法将带约束的优化问题转化为无约束优化问题;为避免在可行域边界出现粘滞现象,引入扰动因子,保证迭代点始终位于可行域内部,推导加扰动的KKT条件;牛顿法求解KKT条件的修正方程,其高度稀疏性会导致MATLAB求解时极大耗费时间,为提高计算效率,将其化为简约修正方程[18]再求解。 假设IEEE33节点系统为一条城市配线,共929[11]户居民。选取基准功率100MV·A,基准电压12.66kV,该配线的最低电压要求为0.96 p.u.。假设外部电网有足够大的有功、无功调节能力,可将电源点作为平衡节点,电压设为 1.05 p.u.,其余为 PQ 节点。 将渗透率定义为可调度EVs数量与私家车总量的比值。 算法采用MATLAB语言编写程序,在Lenovo(2.7 GHz,4G)/PC 机上完成仿真,收敛精度设为 10-5。系统拓扑图及负荷数据见图1和表1。 表1 IEEE 33节点系统负荷Table 1 Loads of IEEE 33-bus system a.充电负荷优化结果。 50%渗透率下典型节点优化充电负荷如图2所示,可见,充电发生在负荷低谷时段,在峰荷时段几乎不发生充电行为,有效起到“填谷”的作用,避免了峰值叠加。 图2 50%渗透率下典型节点优化充电负荷Fig.2 Optimal charging loads of typical node with 50%penetration b.系统负荷分析。 50%、100%渗透率下负荷曲线分别如图3所示,由图可见,无EVs接入时,系统负荷曲线是典型的双峰曲线,在 11∶00、20∶00 出现午高峰及晚高峰,负荷波动较大;而EVs的随机接入充电,使得峰值叠加,在晚高峰尤为严重,恶化了系统负荷曲线;在有序充电情况下,充电负荷集中在谷荷时段,有效避免了峰荷的叠加。随着渗透率的增加,有序充电使负荷曲线逐渐趋于平滑,提高了系统运行的经济性。 图3 负荷曲线Fig.3 Load curves 图4 50%渗透率下系统电压Fig.4 Node voltages of system with 50%penetration 50% 渗透率下 01∶00、20∶00 系统电压(标幺值)如图4所示,在01∶00,有序充电的电压幅值反而低于随机充电。有序充电情况下,会调度较多的EVs在该时刻充电,引入了较大的充电负荷,造成整个系统节点电压下降。但该时刻系统最低电压为0.993 p.u.,仍满足系统节点电压的要求。在20∶00,有序充电情况下几乎无充电行为发生,节点电压曲线与未接入EVs时的重合。而随机充电使电压曲线大幅降低,最低值出现在系统末端 18 号节点,为 0.954 p.u.,无法满足该系统对电压质量的要求;有序充电时该节点电压为 0.968 p.u.,相比于无序充电,末端电压上升了1.4%,提高了末端节点的电压水平,满足系统电压质量要求。 50%渗透率下18号节点的电压(标幺值)如图5所示,由图可见,有序充电使得末端18号节点各时刻的电压曲线更加平缓,提高了负荷高峰时段的电压,降低低谷时段的电压,减小了电压差。随机充电大幅恶化了配网末端节点电压的特性。 图5 50%渗透率下18号节点的电压曲线Fig.5 Voltages of bus 18 with 50%penetration 表2 展示了不同渗透率情况下随机充电与有序充电的潮流结果对比(表中最低电压为标幺值)。结果表明:优化充电状态下,系统最低电压始终为0.968 p.u.,保证了该系统电压的质量要求,不会造成系统电压的恶化。而随机充电下,随渗透率的增加,电压逐渐降低,甚至不能满足系统电压要求。当100%接入时,有序充电相比于随机充电,一日内可减少电能损耗190.5 kW·h。可估算,该系统一年可节约电量约69532.5 kW·h。对于整个电网,通过优化调度充电产生的效益将非常可观。 表2 多种渗透率下随机充电与有序优化充电结果对比Table 2 Comparison between random charging and optimized charging for different penetrations 该配线的电压要求不低于 0.96 p.u.;当线路潮流超过未接入EVs情况下平均潮流的50%时,认为线路重载;节点有功负荷超过式(9)的上限时判定为配变过载。表3给出了峰荷20∶00在随机充电和优化充电下的运行状况,以节点电压越限、线路重载、配变过负荷的数量与相应总数量的比值表示。结果表明,随机充电情况下,在峰荷时段会出现短时电压越限、线路重载、配变过载,优化后则避免了上述状况发生。 表3 20∶00随机充电与有序优化充电下的系统运行状况Table 3 Comparison of system operating conditions between random charging and optimized charging at 20∶00 采用3个系统验证模型的通用性及算法的有效性,由表4中可见,随着系统规模的增大,迭代次数并没有大幅增加,算法具有良好的收敛特性,优化降损效果显著。 表4 50%渗透率下3个系统的测试情况Table 4 Test results of three systems with 50%penetration 采用原-对偶内点法求解配电网层次的家用EVs充电优化问题能有效地实现充电策略的优化计算,具有良好的收敛特性和优化效果。随着智能电网技术的进一步发展,利用本文的优化理论,还可研究配网中考虑EVs放电、无功优化、EVs与其他分布式能源的最优协调出力等问题,并可适用于研究系统负荷波动方差最小、考虑分时电价情况下的车主利益最大化等不同优化目标场景。另外,本文研究对象是中压配电网层次,认为在节点配变处有一个多辆EVs的集聚体,在后续的工作中可研究三相低压配电网层次的EVs优化充电策略,将涉及到每台车辆的优化充电调度。

2 EVs优化充电策略
2.1 充电优化模型

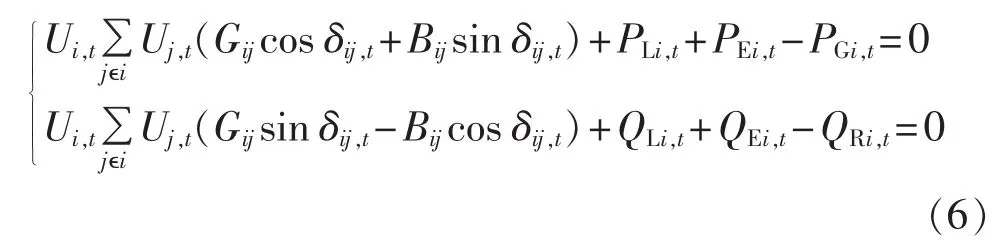

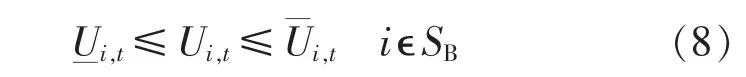

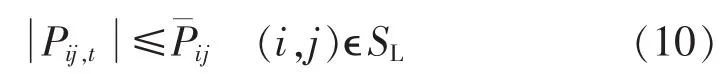


2.2 EVs充电优化调度的实现

3 原-对偶内点法
4 算例仿真

4.1 负荷分析

4.2 电压分析

4.3 潮流结果分析



5 结论与展望

