基于电流源型PWM整流器的高效电池充电系统设计

郭 强 ，刘和平 ，彭东林 ，张 毅 ，刘 庆

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.重庆理工大学 机械检测技术与装备教育部工程研究中心，重庆 400054）

0 引言

随着城市环境与石油资源问题的日益严重，人们对电动汽车相关技术领域的研究日益增加［1］。而作为高效储能装置的动力电池，已成为电动汽车主要动力源。在现有不同种类电池中，因磷酸铁锂电池具有功率、能量密度高，充、放电率大，循环寿命长以及安全性好等优点被应用于电动汽车，以替代镍氢、铅酸蓄电池［2］。

传统燃油汽车可在短时间内完成加油，然而如何高效、安全地实现电动汽车能量的补充，已成为当前研究的热点问题［3-5］。现有充电方法中，恒压（CV）、恒流（CC）和恒流-恒压（CC-CV）这3种充电策略使用最为广泛［6］。CV充电因其结构简单、成本低，在商业产品中得到广泛的应用，但充电电流相对较小，导致充电时间较长。为了缩短充电时间，提出了CC充电策略，然而由于CC充电很难准确判断电池是否充满，容易引起电池过充或欠充，造成电池性能下降。结合CV充电与CC充电的优点，形成了CC-CV充电策略。CC-CV充电策略起始采用CC充电，当电池端电压达到设定值时，即转换为CV模式进行补足充电。当采用大电流充电时，电池极化严重，端电压将较快达到转换电压值，虽然缩短了CC充电段的时间，但同时增加了CV充电时间，使总充电时间基本不变，因此，不能满足快速、高效的充电要求。

目前，大功率电动汽车电池充电器通常采用两级结构。前级采用电压型整流器实现功率因数校正与谐波抑制，而后级采用并联DC-DC变换器实现电压变换与隔离。由于该结构需要模块均流控制，导致系统控制复杂。此外，充电器接地点与车体之间为浮地状态，且SAE J1772中对电池与电网之间是否需要隔离无明确要求［7］。

电流源型整流器CSR（Current Source Rectifier）具有功率因数可调、网侧谐波电流抑制、电流直接控制、结构简单以及降压输出等特点。因此，利用三相CSR拓扑能够实现单级AC-DC降压变换，继而满足非隔离-高效-大功率电池充电器的要求。

针对上述不足，文献［5］和［8］提出一种改进CCCV充电策略，通过检测电池荷电状态（SOC）来实现2种模式的转换。然而该方法需要实时精确检测电池SOC值，为此需要引入较为复杂的SOC估计算法［9］。文献［10］基于超稀疏矩阵变换器提出了一种新颖的模糊控制策略，以实现高电能质量充电。但由于该拓扑自身结构导致损耗增加，当被应用于大电流快速充电场合时，将引起系统效率降低。文献［11］设计了用于动力电池组测试的CSR结构，并提出了基于d-q坐标变换的双闭环电流控制策略，然而，文中仅涉及CC充电策略。

本文采用三相CSR作为电池充电系统拓扑结构，在传统CC-CV充电策略基础上，提出一种基于模糊控制策略的CC、CV模式切换算法。针对2种控制模式，建立了具有电压定向延迟角修正功能的间接电流控制策略。通过对CV模式下控制环路的分析，考虑数字时间延迟对系统的影响，利用MATLAB/SISO设计工具，分别对电流内环与电压外环控制器零点位置与环路增益进行优化。最后，通过仿真与实验验证了上述方法的正确性。

1 CSR系统结构与调制策略

三相CSR主拓扑结构如图1所示。整流器通过滤波电感L、电容C组成二阶低通滤波器与电网相连，起到滤除高频开关分量的作用。开关器件Sij（i=a，b，c；j=1，2）采用 IGBT 与二极管串联结构，以提高器件电压反向阻断能力；在输出侧并联二极管VDW，直通状态时电流经VDW续流，不仅有效防止因整流器开关管故障而引起的直流侧开路，且能减小导通损耗、简化控制逻辑。此外，为了平滑输出电流，在直流侧串联电感Ldc。

假设网侧电压三相平衡且正弦化，有：

其中，Um为网侧相电压峰值；ω0为电网基波角频率。

电流空间矢量定义为：

其中包括6个有效电流矢量和3个电流零矢量，分别对应不同的开关组合状态［12］。

在不改变CSR系统开关频率的情况下，将传统矢量控制中的6分区增加至12分区，可明显缩短器件间的换流过程，从而降低开关损耗［13］。图2给出了三相电网电压与扇区分配关系，根据扇区的不同合理选择有效矢量与零矢量以及矢量间的作用顺序。

当参考矢量落在扇区1内时，三相网侧电压存在关系：ea＞0＞eb＞ec，相应的有效矢量与零矢量分别为 I1［Sa1，Sb2］、I2［Sa1，Sc2］、I0［VDW］。在扇区 1 内，一个开关周期Ts中，参考电流矢量Iref满足：

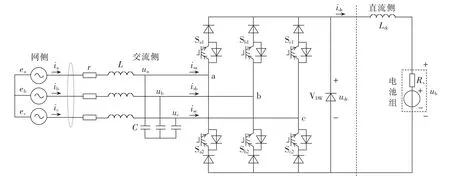
图1 三相CSR拓扑结构Fig.1 Topology of three-phase CSR

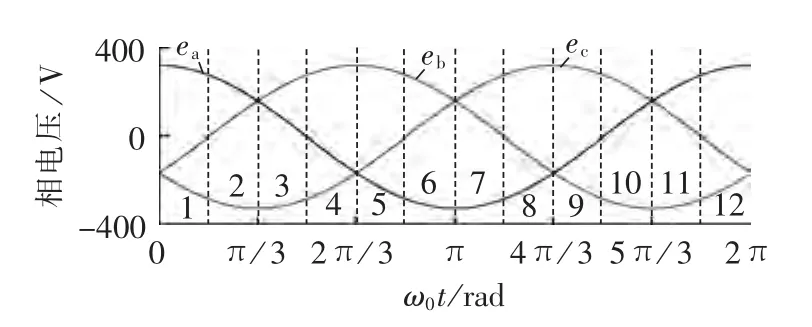
图2 电网电压与扇区的关系Fig.2 Relationship between grid voltage and sector

其中，T1、T2、T0分别为有效矢量 I1、I2及零矢量 I0的作用时间；δ为电流矢量在扇区内的相对扇区角；mc为调制因数，mcє［0，1］；Im为网侧电流峰值；idc为直流侧电流。

当 I1作用时，udc=eab；当 I2作用时，udc=eac；而当 I0作用时，忽略二极管压降，udc=0，则一个开关周期内的直流侧电压为：

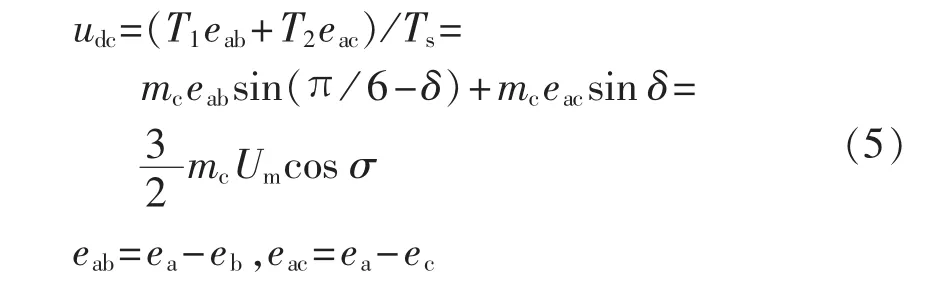
其中，cos σ为网侧功率因数。

2 2种非隔离型充电系统损耗比较

三相电压源型整流器 VSR（Voltage Source Rectifier）为升压型变换器，其输出母线电压通常高于650 V，而电动汽车动力电池组电压范围一般在48～400 V之间。为了实现与电池组之间的电压匹配，需要在整流器输出侧增加一级DC-DC降压变换器，而对于大功率非隔离充电系统，其后一级常采用交错并联Buck变换器［14-15］，如图3所示。与VSR不同，三相CSR不仅能够输出恒定的直流电流，且其输出电压在0～3Um/2范围内可调。以下从功率损耗角度对2种非隔离型充电系统进行比较分析。

图3 n相交错并联Buck变换器Fig.3 n-phase interleaved Buck converter

相同负载功率（350 V/30 A）情况下，三相CSR和三相VSR+交错并联Buck变换器（VSR-IBC）的损耗分布图如图4所示。其中，PLdc、PLac，cs、PDF，sw、PDF，con、PDS，sw、PDS，con、PS，sw、PS，con分别为三相 CSR 中直流侧电感损耗、交流滤波电感损耗、反向续流二极管开关损耗、导通损耗、串联二极管开关损耗、导通损耗、开关管开关损耗、导通损耗；PLac，vs、PVD，sw、PVD，con、PVS，sw、PVS，con分别为三相VSR中滤波电感损耗、开关管开关损耗、导通损耗、并联二极管开关损耗、导通损耗；PLB为Buck电路中的电感损耗；PBuck，sw为Buck电路中IGBT和二极管开关损耗之和；PBuck，con为 Buck电路中IGBT和二极管导通损耗之和。通过对2种非隔离充电拓扑的效率比较可看出，CSR具有更高的效率，达到97.24%；而VSR-IBC效率降低的原因主要是由于Buck电路中开关管所承受的电压应力较大，致使开关损耗显著增加，占总损耗的27%。

图4 2种拓扑结构的损耗分布和效率比较Fig.4 Loss distribution and efficiency of two topologies

对于要求更高输出功率、更高输出电流的场合，CSR直流侧电感设计将愈发困难，但通过采用三相CSR多模块并联结构，可将直流侧大电感变成多个分立小电感，从而能够减小电感的体积、提高系统效率与功率密度。

不仅如此，VSR-IBC为两级拓扑结构，在控制上较CSR复杂。综上所述，三相CSR非常适合作为非隔离动力电池快速充电系统的拓扑结构。

3 系统控制策略

三相CSR充电系统控制框图如图5所示，主要由CC-CV充电控制环节、功率因数控制环节组成。

3.1 功率因数补偿策略

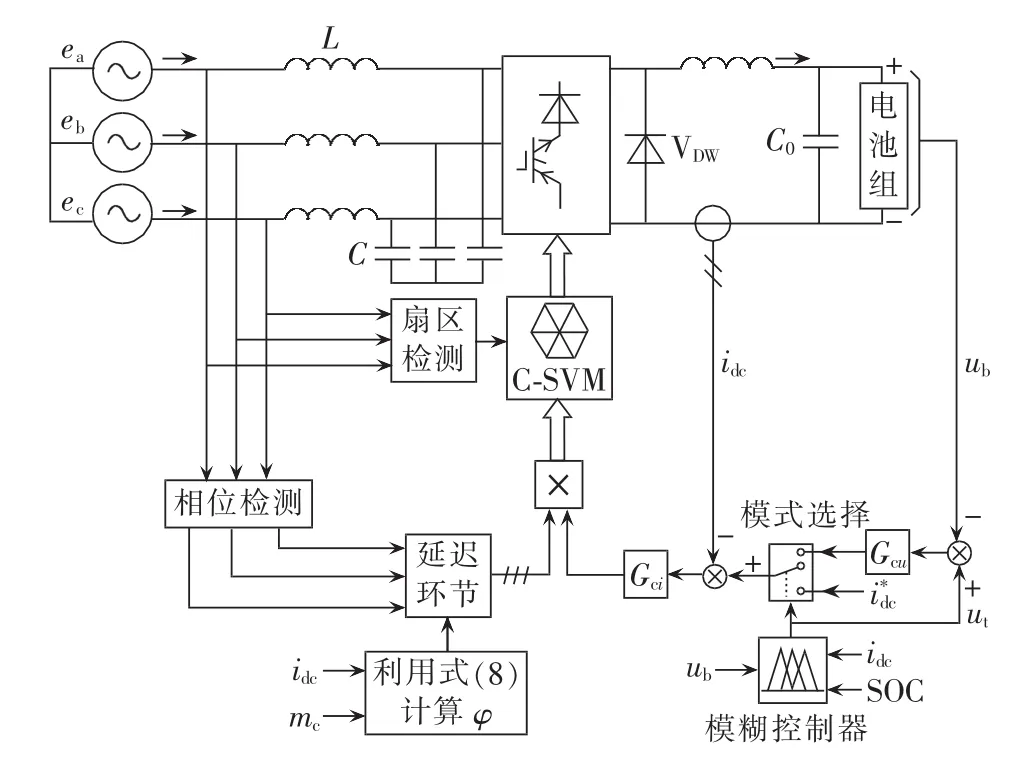
图5 三相CSR充电系统控制策略Fig.5 Control strategy of three-phase CSR charging system

直接电流控制因采用双闭环控制策略，其抗扰动性能及电流跟随性较好，但需增加交流侧电流传感器，成本相应增加；而且双闭环系统中PI控制器参数相互影响，调试复杂。当参数匹配不佳时，其输出性能并不一定优于间接电流控制策略。当CSR的主电路参数一定时，间接电流控制同样可以很好地实现网侧电流的控制，其控制方法简单、成本低，故可适用于三相CSR的控制。

为便于分析，忽略电路中的寄生电阻，三相CSR交流侧可等效为单相结构（以a相为例）［16］，如图6所示，其中交流侧电流等效为电流受控源的形式。

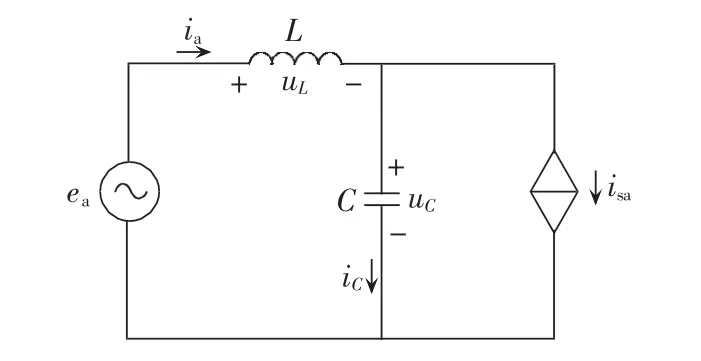
图6 三相CSR交流侧等效电路Fig.6 AC-side equivalent circuit of three-phase CSR

考虑系统中PWM开关频率远大于电网频率时，忽略交流侧电流以及电容电压的高次谐波分量，有：

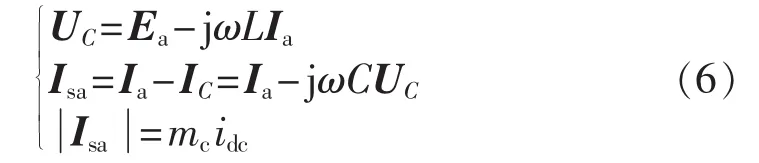
其中，UC为电容电压矢量；Ea为整流器a相电网电压矢量；Ia为网侧电流矢量；IC为电容电流矢量；Isa为交流侧电流矢量。

假设CSR充电系统处于单位功率因数运行状态，网侧电流与电网电压同相位，根据图6以及式（6），并基于相量法作出a相基波空间矢量图，见图7。

根据图7利用几何原理，得到如下等式：

图7 CSR空间矢量图（a相）Fig.7 Space vector chart of CSR（phase-a）

联立式（6）和（7）得到：

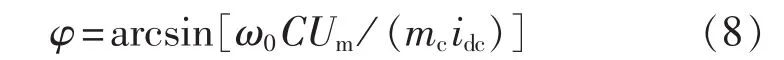
由式（8）不难看出，当系统工作在单位功率因数时，交流侧电流滞后角φ与电网频率、滤波电容C、网侧电流峰值Um成正比，与直流侧电流idc、调制因数mc成反比。当电网电压和电容C保持不变时，根据CSR系统的运行工作点（idc与mc），容易计算出滞后角φ。然后，通过对网侧电压信号进行延迟修正，即得到正确的相位指令信号，从而实现网侧单位功率因数控制。

3.2 电池CC-CV充电控制策略

对于CC-CV充电模式，其转换电压直接决定电池充电速度与循环寿命。当转换电压设置较高时，电池在恒流阶段可以充入更多电量，从而缩短总的充电时间；然而过高的转换电压将显著降低电池的循环寿命［17］。不仅如此，转换电压还与电池放电深度有关［18］，当电池放电深度越大时表明其可接受充电电流越高，故可适当提高转换电压以提高充电效率，反之亦然。因此，针对上述问题本文提出一种基于模糊控制策略的CC-CV充电模式切换算法，即依据电池内部反应机理与外部充放电特性，通过初始SOC、充电电流智能实现2种充电方式之间的转换。

选取电池初始SOC（记作SOC0）、充电电流idc作为模糊控制器的输入量，模式转换电压ut作为模糊控制器的输出量。输入量SOC0物理论域为［0，1］，定义 5 个语言值，其模糊集为｛VL，L，M，H，VH｝；输入量idc物理论域为［0 A，150 A］，定义7个语言值，其模糊集为｛VL，L，RL，M，RH，H，VH｝；输出量 ut物理论域为［24.5 V，27.3 V］，同样定义7个语言值，其模糊集描述与输入量idc一致。其中，VL表示很低；L表示低；RL表示较低；M表示中；RH表示较高；H表示高；VH表示很高。上述隶属度函数均采用梯形分布，输入输出隶属度函数见图8。同时依照经验与实验测试数据，建立模糊控制规则见表1，表中第一行为idc的语言值。控制器采用极大-极小运算规则进行模糊推理，而去模糊化采用面积中心法［19］。

输入输出关系的三维效果图如图9所示，可以看出，模糊控制器根据系统输入量SOC0与idc，通过模糊控制规则获得相应的模式转换电压，摒弃了常规充电模式中仅依据固定电压作为电池充电结束的单一化判据，从而在不影响电池寿命的前提下，实现对电池组的高效快速充电。

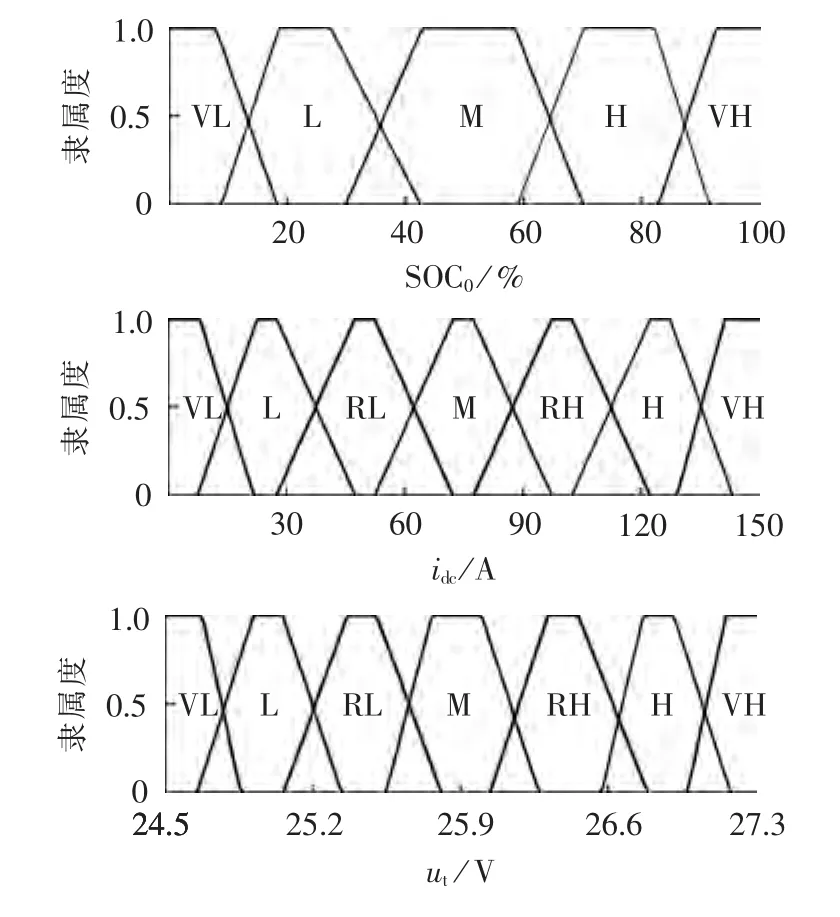
图8 输入、输出变量隶属度函数Fig.8 Membership function of input and output variables

表1 模式转换电压模糊规则表Table 1 Fuzzy rule of mode switching voltage

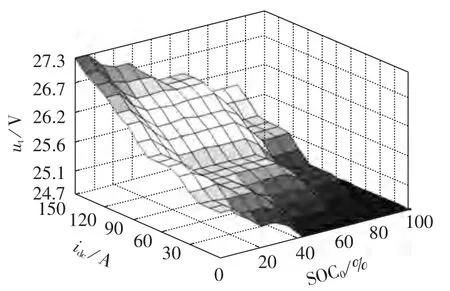
图9 模糊控制器输入、输出关系Fig.9 Relationship between input and output of fuzzy controller

3.3 CC-CV控制环路设计

CV充电模式时，系统通过控制输出电压来调节输出电流，故需要电压外环与电流内环级联控制结构［20］；而CC充电模式时，即采用单闭环控制结构。由于CC控制环路即为CV控制的电流内环，为了避免冗余，文中仅针对CV模式控制环路进行设计，控制框图见图10。其中虚线框内表示电流内环控制环路，由于控制量均为直流量，故采用PI控制器，即：

其中，KP1、KI1分别为电流内环控制器比例系数与积分系数。

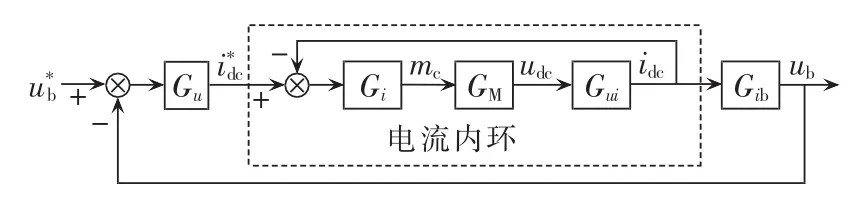
图10 CV控制模式下系统闭环控制框图Fig.10 Block diagram of close-loop control system in CV mode

当CSR工作在单位功率因数时，考虑系统数字时间延迟，结合式（5）求得传递函数 GM（s）的表达式为：

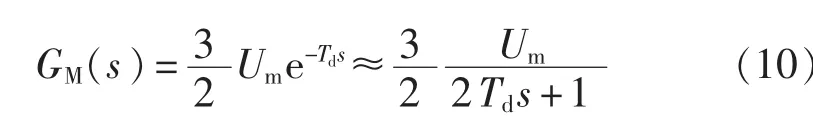
其中，Td为延迟时间。

图10 中，Gui（s）为直流侧电流idc到输出侧电压udc的传递函数，即：

其中，Rs为电池内阻；C0为直流侧电容。

联立式（9）—（11），得到电流内环开环、闭环传递函数为：

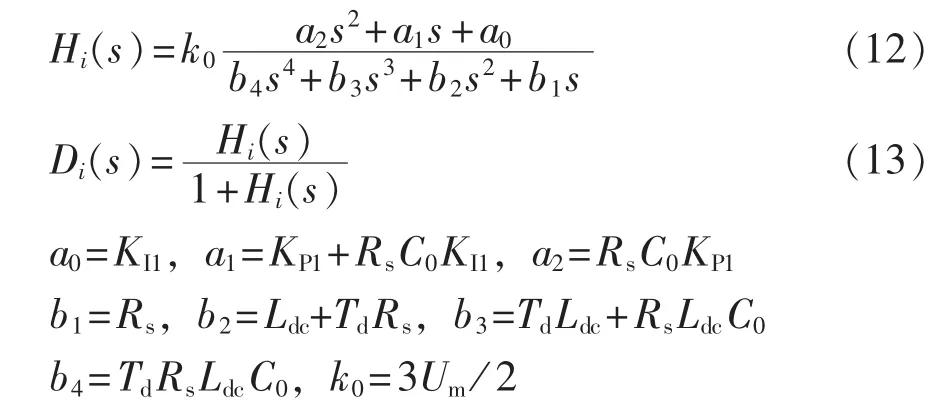
由式（12）可知，电流内环开环传递函数为四阶系统，当系统参数确定时，若使电感电流准确追踪给定值，需要合理设置控制器Gi（s）参数。利用MATLAB /SISO 设计工具，通过合理配置 Gi（s）中零点位置与比例增益，兼顾系统的动态与稳态性能，最终确定控制器参数KP1=0.3、KI1=18.1。相应得到补偿后电流内环开环、闭环Bode图，如图11所示。其中，开环传递函数的相位裕度为57.8°，截止频率为667 Hz；相应闭环传递函数的系统带宽为1060 Hz，约为开关频率的1/10。因此，设计出的电流内环能够满足系统性能的要求。

图11 电流内环开环与闭环传递函数Bode图Fig.11 Bode diagrams of open-and close-loop transfer functions of inner current loop

通常情况下，电池在充电过程中其端电压变化缓慢，同时为了避免电压外环与电流内环之间相互干扰，电压外环的带宽应远小于电流内环带宽［21］。因此，在设计电压外环时，将电流内环近似等效为一阶延时环节，即：

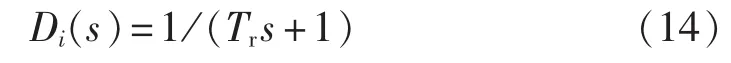
其中，Tr为电流内环等效时间常数，通过近似曲线拟合，Tr=2e-4s。

电压环路中Gib（s）为电池电压ub到直流侧电流idc的传递函数，有：

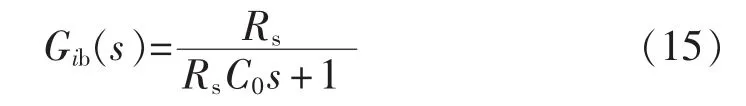
同理，电压外环控制器Gu（s）采用PI控制器，分别得到电压外环开环、闭环传递函数：

其中，KP2、KI2分别为电压外环控制器 Gu（s）的比例系数与积分系数。

同样利用MATLAB/SISO软件工具对控制器Gu（s）的参数进行设计优化。为了避免电流内环与电压外环之间相互干扰，最终确定外环控制器参数KP2=0.1、KI2=3060。由图12不难看出，此时相位裕度为82°，截止频率为106 Hz，系统带宽为 124 Hz，满足电压外环性能的设计要求。

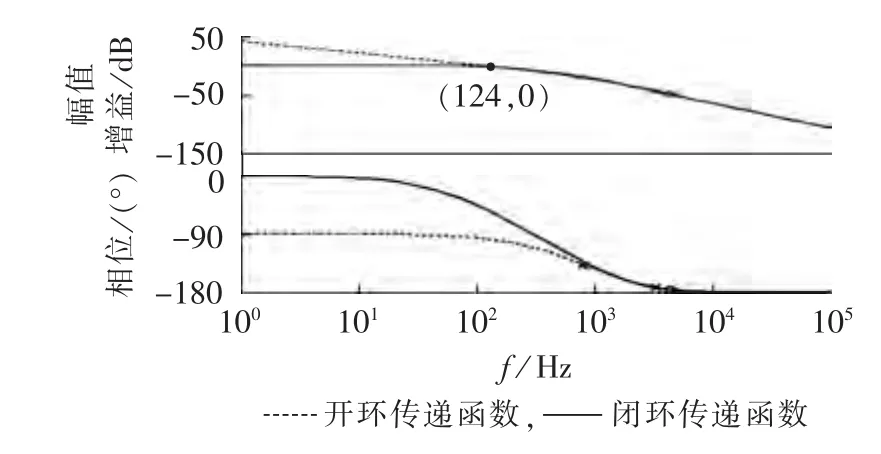
图12 电压外环开环与闭环传递函数Bode图Fig.12 Bode diagrams of open-and close-loop transfer functions of outer voltage loop

4 仿真和实验

4.1 仿真结果分析

为了验证所提出方法的正确性，借助MATLAB/Simulink软件搭建三相CSR充电系统的仿真模型。其中电路仿真参数见表2。

表2 CSR主要参数Table 2 Main parameters of CSR

三相CSR工作在恒压模式时，其仿真结果如图13所示。以a相为例，网侧输入电流与电网电压同相位，且正弦化；输出侧电流平滑，输出电压保持恒定；功率因数较高，大于0.99；网侧电流THD值为2.30%，满足IEEE519标准。

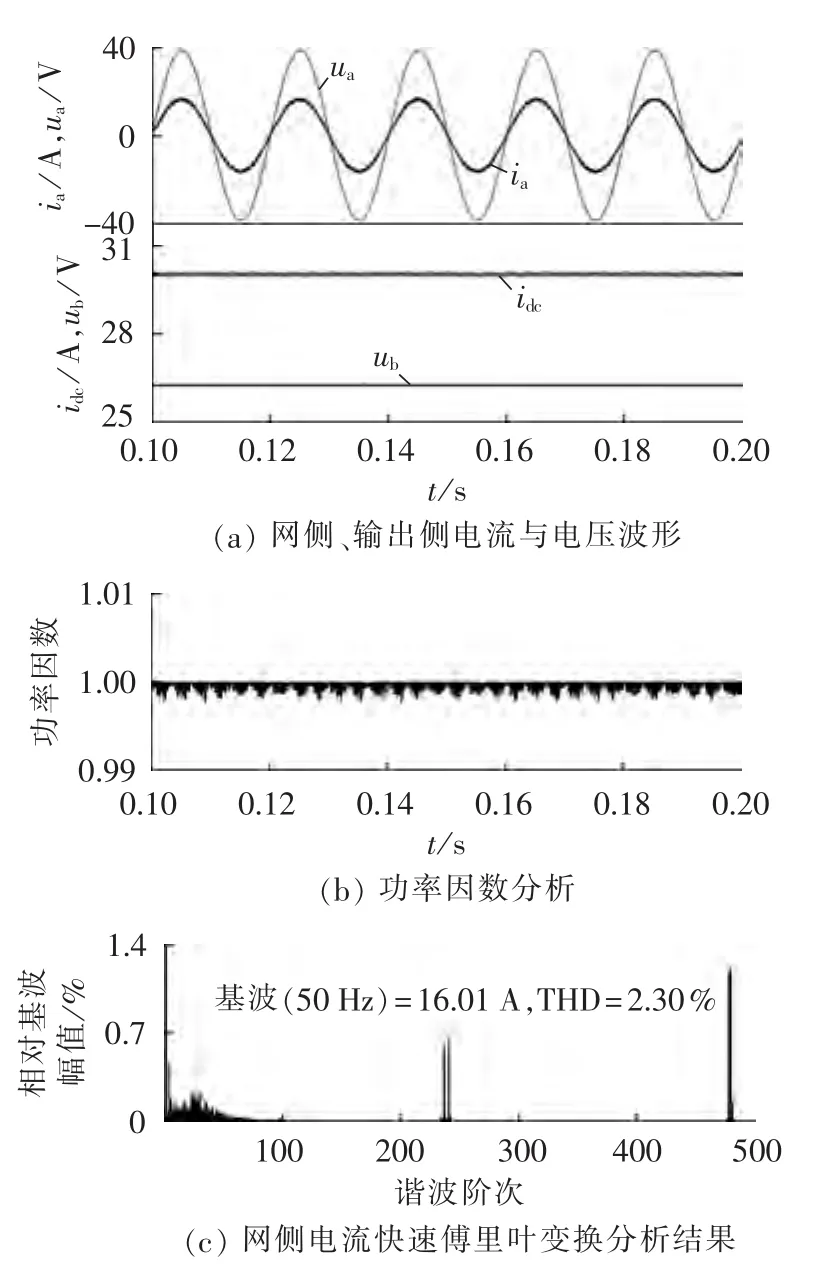
图13 恒压充电运行模式仿真结果Fig.13 Simulative results of charging operation in CV mode

4.2 实验结果分析

搭建一台三相CSR充电系统实验样机，其中，功率开关管和二极管分别采用三菱PM400HSA120和RM300HA-24F，主控芯片采用TI公司TMS320F2812。

图14给出CC、CV充电模式下，稳态运行时的网侧电流、电压，以及网侧电流的快速傅里叶变换分析结果，其中ua为电压采样后的调理信号。图14（a）为CC充电过程，此时充电电流给定值为100 A，实测电池端电压ub=24.5 V；图14（b）为CV充电过程，因电池SOC0=0，CC值为100 A，模糊控制器经推理得到此时 CV值设定为ub=26.30 V；图14（c）为CV模式时对网侧电流快速傅里叶变换分析结果，对比图13（c），可以看出网侧电流中低频谐波含量较高，主要是由实际电网电压中低次谐波分量经迭代作用造成的。实验结果表明，2种充电模式下，网侧电流均能保持单位功率因数，正弦化程度较高，且THD限制在5%以内；直流侧电流平滑、纹波较小，与仿真结果一致，从而验证本文所提出的充电系统具有良好的输入、输出性能。

图14 2种充电模式下电网电压、电流以及电流FFT分析结果Fig.14 Grid-voltage，grid-current and grid-current FFT analysis for CC and CV modes

图15给出了充电系统在整个充电过程中的电压、电流变化曲线，总充电时间为152 min。初始阶段，以100 A进行快速CC充电，当电池端电压上升到26.30 V时，系统由CC模式切换至CV模式；该模式下充电电流随时间不断减小，当电流下降为20 A时，整个充电过程结束；停充后由于电池极化现象消失，电池端电压逐渐降低并趋于稳定。

图15 充电全过程电压、电流曲线图Fig.15 Waveform of voltage and current for whole charging process

5 结论

本文采用三相CSR作为充电系统拓扑结构，在传统CC-CV充电策略基础上，依据电池电化学特性，提出一种基于模糊推理控制策略的模式切换算法。建立了具有电压定向延迟角修正功能的间接电流控制策略，采用频域法对CV模式下控制环路进行分析，并对电流内环与电压外环控制器零点位置与环路增益进行优化。通过仿真分析与实验验证，得到如下结论。

a.采用具有延迟角修正功能的间接电流控制策略，不仅改善了因LC滤波器对系统功率因数的影响，而且无需坐标变换与锁相环检测环节，降低了系统的计算量。

b.提出一种基于模糊控制策略的CC、CV充电模式切换算法，即依据电池内部反应机理与外部充放电特性，通过SOC0、充电电流智能实现2种充电方式间的转换。

c.仿真和实验结果表明，本文所提出的充电系统在CC/CV模式下，输入侧实现了单位功率因数校正、电流正弦化以及较低的电流谐波畸变率；输出侧实现了CC控制或CV控制；并且实现了CC模式和CV模式之间的智能切换，兼顾电池寿命与充电效率。