充换电服务网络动力电池配送最优路径建模方法

刘晓胜，张 芮，朱宏林，王 娟

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

电动汽车相对于传统汽车具有明显的节能减排的特点，成为21世纪最具有潜力的交通工具［1］。但续航里程是制约电动汽车发展的主要因素。动力电池作为电动汽车的动力来源，快速更换电池是解决这种问题的有效途径之一［2］。对动力电池配送车辆进行路径优化，不仅可以提高经济效益，还可以及时满足电动汽车的能量供给［3］。由此可见，合理选择满足约束条件的动力电池配送最优路径，进一步提升充换电站服务体系运行管理程度，具有非常重要的现实意义［4］。

物流配送中的路径选择优化问题是一个典型的NP-hard问题，国内外学者对其进行了深入的研究，并提出很多求解算法。这些算法可以分为精确求解算法和启发式算法两大类［5］。在精确求解算法中，计算量与问题的规模呈指数增加关系，求解耗费时间相当长，效率低［6］。启发式算法以及一些组合算法成为研究路径优化问题的主要算法［7］，但是为了保证可行解，导致遗传算法爬山能力差、禁忌搜索算法全局性差等问题。基本的启发式算法在求解大规模的路径优化问题时存在各种缺陷［8］。

蚁群算法是一种新的种群启发式算法，可以看作是一个分布式的多智能体系统。它可以在问题空间的多点同时独立进行解搜索，具有很强的鲁棒性［9］。本文根据路网的特点对蚁群算法进行改进，同时为了避免算法在搜索过程中陷入局部最优，在算法中引入惩罚因子，在保证全局最优的同时还可以提高算法的收敛速度。而且，对于城市的实际路网，当交通网络规模庞大，各服务点的服务范围内交通情况实时变化时，蚁群算法在动态环境中具有良好的灵活性［10］，能够适应不断变化的道路状况对路径选择的影响。同时，正反馈可以缩小搜索范围，保证算法朝着最优解的方向进化［11］，进一步体现了蚁群算法在求解路径优化问题时的优越性。

1 电池配送的数学模型

本文以杭州市充换电服务网为背景，从电池配送的实际问题出发，主要解决以下2个问题。

a.电动汽车在行驶过程中可能会出现电力不足，而不能到达配送站进行电力补充。这时，电动汽车车主可以向电池调配中心“报警”，电池调度中心记录有关的道路地理信息数据，然后调度载有动力电池的抢修车在最短的时间内到报警现场抢修。

b.电动汽车换电主要依赖于智能充换电服务网络，智能充换电服务网络主要由电池集中充电站、电池充换电站及电池配送站三级网络组成［12］。动力电池作为电能的载体，流动于三级服务网络之间。由于充换电站的电池基本上可以自给，因此本文主要解决从集中充电站（物流据点）用多辆汽车向配送站（客户点）送货的问题，每个需求点的位置和需求量一定，每辆配送车的载重量一定，每日的最大行驶里程一定，合理安排配送车路线，使总运距最短，从而使配送成本最小。

1.1 抢修系统的数学模型

在对路径进行选择时，人们往往更倾向于选择顺畅、宽敞的大道，这样抢修时间比较短；相反，有的路径虽然较短，但可能存在道路狭窄等问题，甚至经常发生交通拥堵，因而时间花费和燃油花费均不理想。因此，人们在选择较为合理的路径时主要考虑时间最短和距离最短。

1.1.1 路网的构建

城市交通主要由众多的道路相交、相连而构成，并组成纵横交错、错综复杂的城市交通网络图。道路拓扑结构是求解最优路径问题的基础，它描述了道路网络结点（道路交叉点）和主要道路的连通关系。提取和构建道路网络的网络拓扑结构是指：运用图论中的相关知识，交通路网被抽象成带权网络无向图G=（V，E，W）。 其中，V 为路网节点（即道路的交叉点）的有穷非空集合，V=｛V1，V2，…，Vn｝；E 为 V 中顶点之间边的有穷集，每一条边表示相邻两节点间的直达路径，假定相邻两节点间最多仅有一条边。SPє V 表示配送站（即源结点），EPє｛V-｛SP｝｝为事故地点（即目的结点），对 G 中的某一条边（Vi，Vj），相应地有一个表示该路段特性的数 di，j，若（Vi，Vj）之间连通则 di，j为实际路段长度；若（Vi，Vj）之间不连通，则 di，j=∞，在实际计算中以一个足够大的值代替。把矩阵称为权值矩阵，Dij表示路径（Vi，Vj）是综合考虑道路属性和交通情况的等效道路长度。W为E上边权值的有穷集，对于一定的城市交通网络，W反映了某一时段的交通状况和道路属性。

利用从杭州市电子地图上提取的道路网络中各路段的属性数据以及各结点的坐标信息，并利用邻接矩阵存储网络拓扑信息，得到如图1所示的道路网络拓扑结构，在不同的区域道路拥堵指数不同。

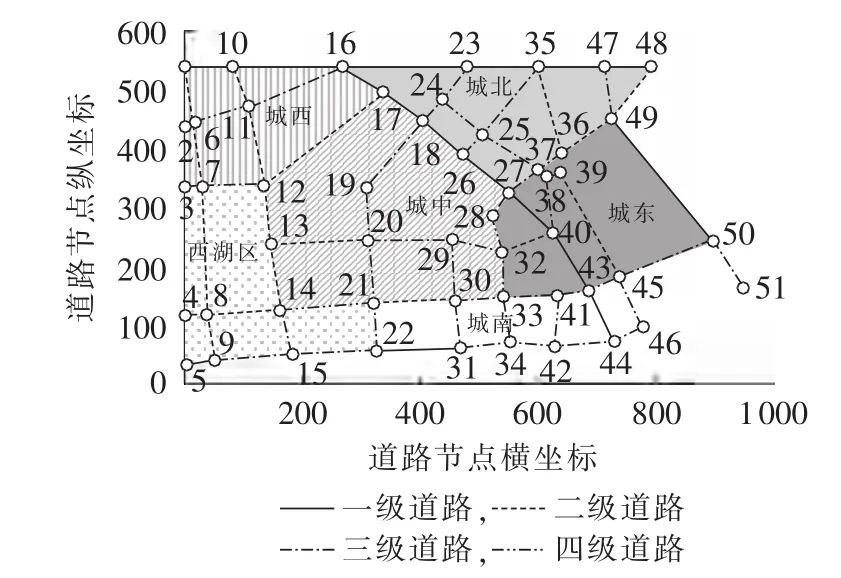
图1 杭州市道路网络拓扑图Fig.1 Road network of Hangzhou

1.1.2 模型建立

在最优路径规划中，增加2个启发因素：道路等级指数rij和表示t时刻道路（Vi，Vj）交通拥堵情况的指数yij（t）。道路等级指数rij指道路的相对重要程度，其取值如式（1）所示：

rij值越小，说明道路（Vi，Vj）越重要，人工蚂蚁在寻优过程中更倾向于选择等级较高的一级道路（快速路）。 yij（t）表示 t时刻道路（Vi，Vj）的交通拥堵情况，yij（t）越小，说明 t时刻道路（Vi，Vj）越通畅，这条路径被选的概率越大。交通拥堵指数的范围是1～10，10表示严重拥堵，1表示完全畅通。由于同一时间段不同区域的交通拥堵情况不同，不同时间段同一个区域的交通情况也不同，本文将一天的交通拥堵情况分成4个时间段和6个区域考虑，如表1［13］所示。某时间段某路段的交通拥堵指数在相应的指数范围内随机变化。在仿真中，利用MATLAB中的rand函数在该范围内随机产生交通拥堵指数的值来模拟实际道路交通情况的随时变化。

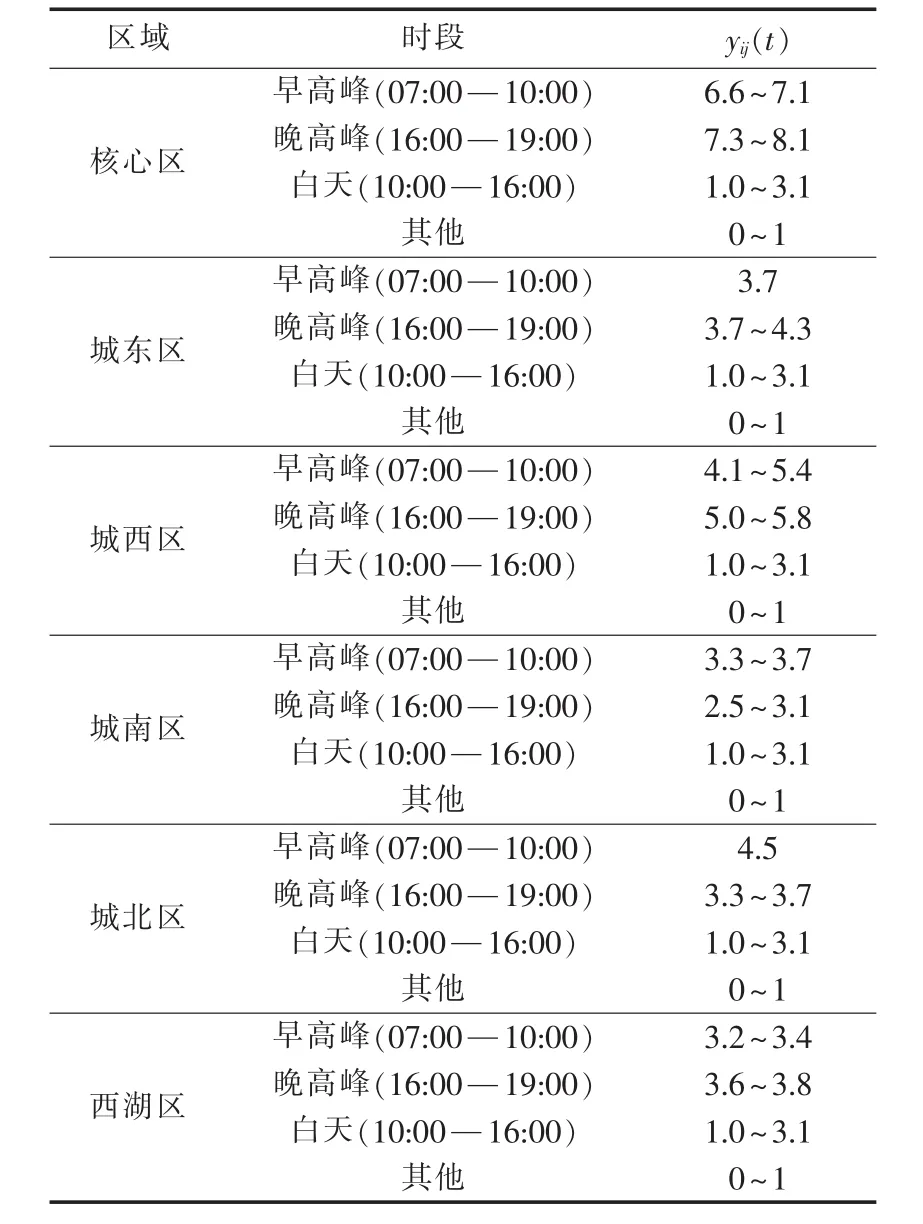
表1 杭州市不同区域不同时间段交通拥堵指数 yij（t）的范围Table 1 Range of congestion index yij（t） of Hangzhou for different regions and different periods

引入3个权重系数来衡量影响最优路径选择的各个因素相对重要程度：路径距离的权重系数W1，道路等级的权重系数W2，交通堵塞的权重系数W3，满足W1+W2+W3=1。利用层次分析法最终确定W1=0.6191、W2=0.1506、W3=0.3715。根据前面的分析，本文将时间约束、道路交通状况等添加到目标函数中，提出以实际道路长度、道路等级以及交通拥堵情况线性组合成的等效道路长度为目标函数的最优路径规划问题，来规划省时省路的最优路径。最终确定的等效道路长度Dij如式（2）所示：

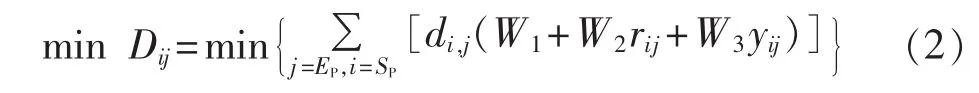
1.2 配送系统的数学模型

1.2.1 模型假设

在进行动力电池配送路径选择的数学模型构造时首先作如下假设：

a.任何配送中心（集中充电站）所对应的需求点（配送站）和任何需求点的需求量均已知；

b.每个需求点（配送站）只由一辆车服务一次，每辆车只能服务一条路线；

c.需求点相互之间以及需求点与配送中心之间距离已知；

d.配送中心拥有多辆同种载重量的车，每辆车始点和终点均为各自所属的配送中心；

e.配送成本与配送距离成正比；

f.要配送的动力电池有2种型号，质量也不同，各型号的配送比例为1∶1，配送质量取平均值；

g.配送网点有足够的资源可以供应配送，并且拥有足够的配送能力；

h.最终目标是寻找一个物流配送的路线，使配送成本最小。

1.2.2 变量定义

模型中要用到的变量定义为：K为集中充电站拥有的配送汽车数目；Qk（k=1，2，…，K）为每辆汽车的载重量；Dk（k=1，2，…，K）为每辆汽车一次配送的行驶距离；L 为配送站（需求点）数目；qi（i=1，2，…，L） 为每个配送站需要的动力电池的数目；di，j（i，j=1，2，…，L） 为配送站 i到配送站 j的距离；d0j（j=1，2，…，L） 为集中充电站到配送站的距离；nk（k=1，2，…，K）为第 k辆汽车配送的配送站数目（nk=0表示未使用第 k 辆汽车）；Rk（k=1，2，…，K）为第 k 辆汽车配送的配送站集合（当 nk≠0 时表示该配送站在第 k 辆汽车的配送线路中顺序为i；ei为客户点i对货物需求的时间窗系数，值越大表示要货的紧急程度越高，当 ei为-1时，表示没有限制到货时间；Pe为超时惩罚系数。

1.2.3 模型建立

配送车最优路径的选择条件是，在满足各个配送站需求的条件下，使整体的配送成本最小。而配送成本基本上和路程成正比，因此本文把寻找最短路径作为目标函数。但是考虑到配送过程中可能由于交通情况配送车不能按时到达配送站，这里引入时间窗系数ei和超时惩罚系数Pe，将等待时间等效成距离，也就是下文提到的超时成本。

总路程S如式（3）所示。

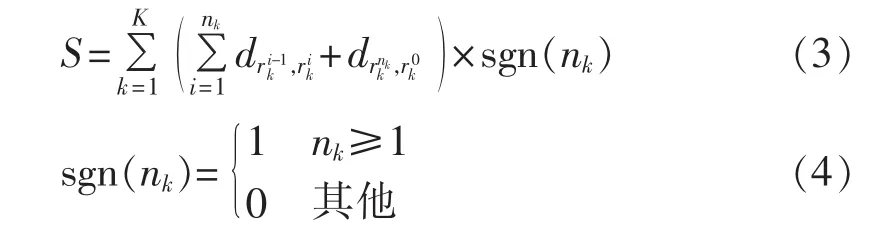
假设集中充电站在第k辆车的配送路径中排在第s位完成配送后，总的超时成本计算如式（5）所示：

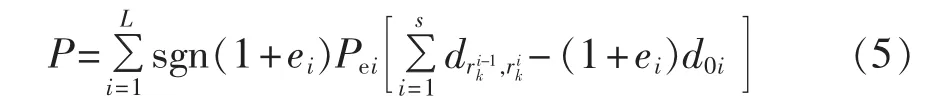
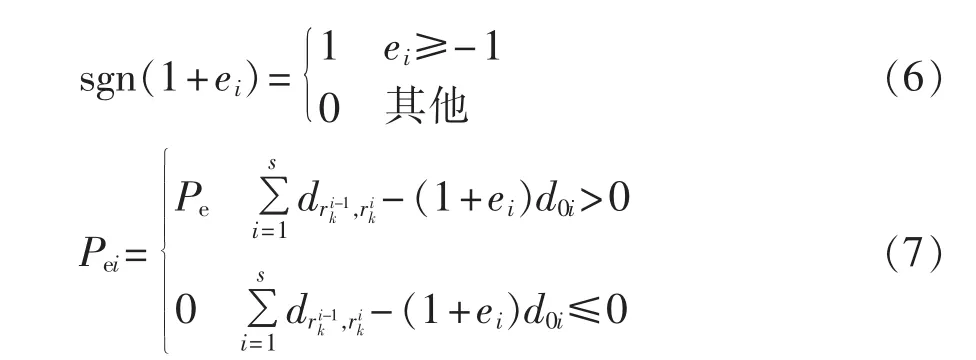
目标函数为：

约束条件为：

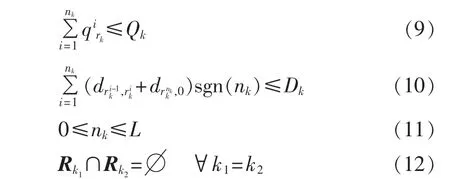
上述模型中，式（8）为目标函数；式（9）保证每条路径上各配送站的电池需求量之和不超过汽车的载重量；式（10）保证每条配送路径的路程不能超过汽车一次配送的最大行驶里程；式（12）限制每个配送站仅能由1辆汽车送货。

2 蚁群算法

2.1 基本蚁群算法

蚁群算法是人工智能算法之一，其模拟蚂蚁的觅食行为，按启发式思想，通过外激素的诱发作用逐渐收敛到问题的全局最优解［14-15］。 设：di，j（i，j=1，2，…，n）表示路网中路段（Vi，Vj）间的距离，m是蚁群中蚂蚁的数量，n为路网中的节点数；τij（t）表示t时刻在路段（Vi，Vj）上残留的信息素浓度。初始时刻，设τij（0）=C（C为常数），即各条路径上信息素浓度相等。人工蚂蚁 k（k=1，2，…，m）在寻优过程中，根据各条路径上的信息素浓度决定转移方向。这里用禁忌表tabuk来记录蚂蚁k当前所走过的节点；E表示所有节点的集合，集合随着tabuk进化过程做动态调整；Ak=｛E-tabuk｝表示蚂蚁k下一步允许选择的节点集合。表示人工蚂蚁k在t时刻由节点i转移到节点j的概率：

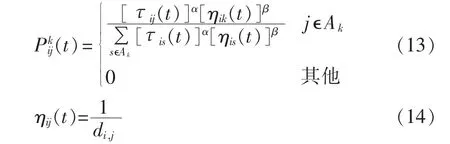
其中，ηij（t）为能见度，在最短路径问题中表示节点i转移到节点 j的启发式信息；α 表示在路径（Vi，Vj）上信息素的重要程度；β表示在路径（Vi，Vj）上启发信息的重要程度。当所有人工蚂蚁均完成对n个节点的遍历（也即1个循环结束），此时禁忌表已经填满，应清空，并将蚂蚁当前所在节点放入禁忌表tabuk中，准备下一次循环。同时，计算每一只人工蚂蚁所走过的路径长度Lk，并保存最短路径。

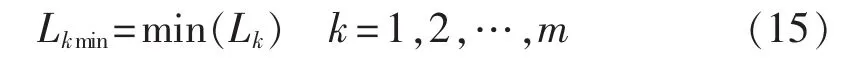
随着时间的积累，以前留下的信息素逐渐蒸发消逝，用参数1-ρ表示信息素残留程度，当所有蚂蚁均完成一次循环后，各条路径上的信息素根据式（16）作调整。

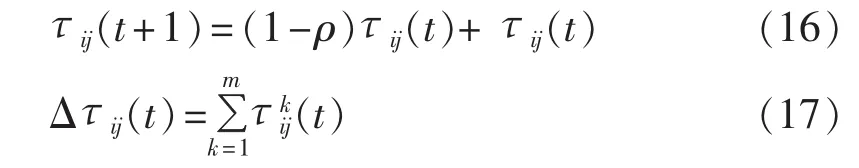
设置周游次数计数器NC，当达到设定值时结束。最短路径为：

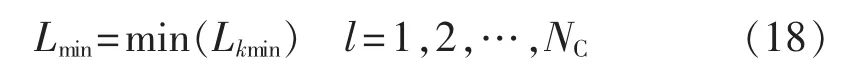
2.2 算法改进

2.2.1 基于路网的算法改进

在基本的蚁群算法中，当蚂蚁从节点i选择下一个节点j时，需要将n-1个节点与禁忌表比较，再计算n-1个节点中不在禁忌表中的转移概率，需要较长的计算时间。在实际应用中，蚂蚁一定是在一个具有拓扑关系的网络中爬行，蚂蚁从节点i选择下一个节点时，不会在所有非禁忌表中的节点间选择，而只能是选择与节点i之间存在直接路径的节点，即存在边（Vi，Vj）的节点中选择。因此，在计算转移概率时，仅需计算这部分节点的转移概率，从而大幅降低了基本蚁群算法的计算量，提高了算法的计算速度。

类似地，在对信息素初始化时，对节点间有相连关系的道路的信息素初始化为τij（0）=C（C为常数，C≠0），对没有相连关系的节点初始化为τij（0）=0。

2.2.2 全局信息素更新策略

道路网络拓扑中会存在一些“死路”，即存在边缘节点。算法对走入死路的蚂蚁进行标记，并记录与边缘节点相连的路径，如图2所示，若蚂蚁在寻找路径过程中走入节点3或者节点4，无法到达终点，称节点3、节点4为边缘节点，同时将路径L23或者路径L14称为死路。

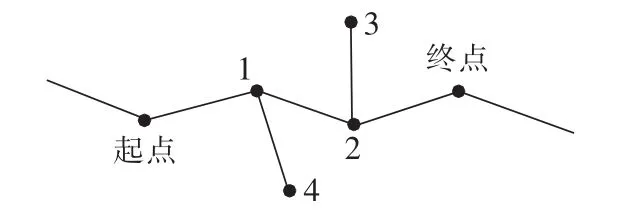
图2 死路和边缘节点说明Fig.2 Illustration of dead-end and fringe-node

为避免下一只蚂蚁在寻找路径过程中进入死路，引入惩罚系数M，范围是0～1。特别说明，这里的惩罚系数M与衰减系数ρ不一样，衰减系数是模拟人体大脑的行为，在新的信息存入大脑的同时，旧的信息会随着时间的推移而衰减，即道路网络拓扑上的所有信息素都会受到衰减系数ρ的作用。但是惩罚系数只作用于与边缘节点相连的道路上的信息素。因此，对走入死路中的蚂蚁所经过的与边缘节点相连的路径，利用τij（t）=τij（t）M，使信息素进一步衰减，减小下一次循环蚂蚁选择该条路径的概率，提高算法的效率。

2.2.3 算法流程图

综上所述，可以得到改进后的算法流程图如图3所示。

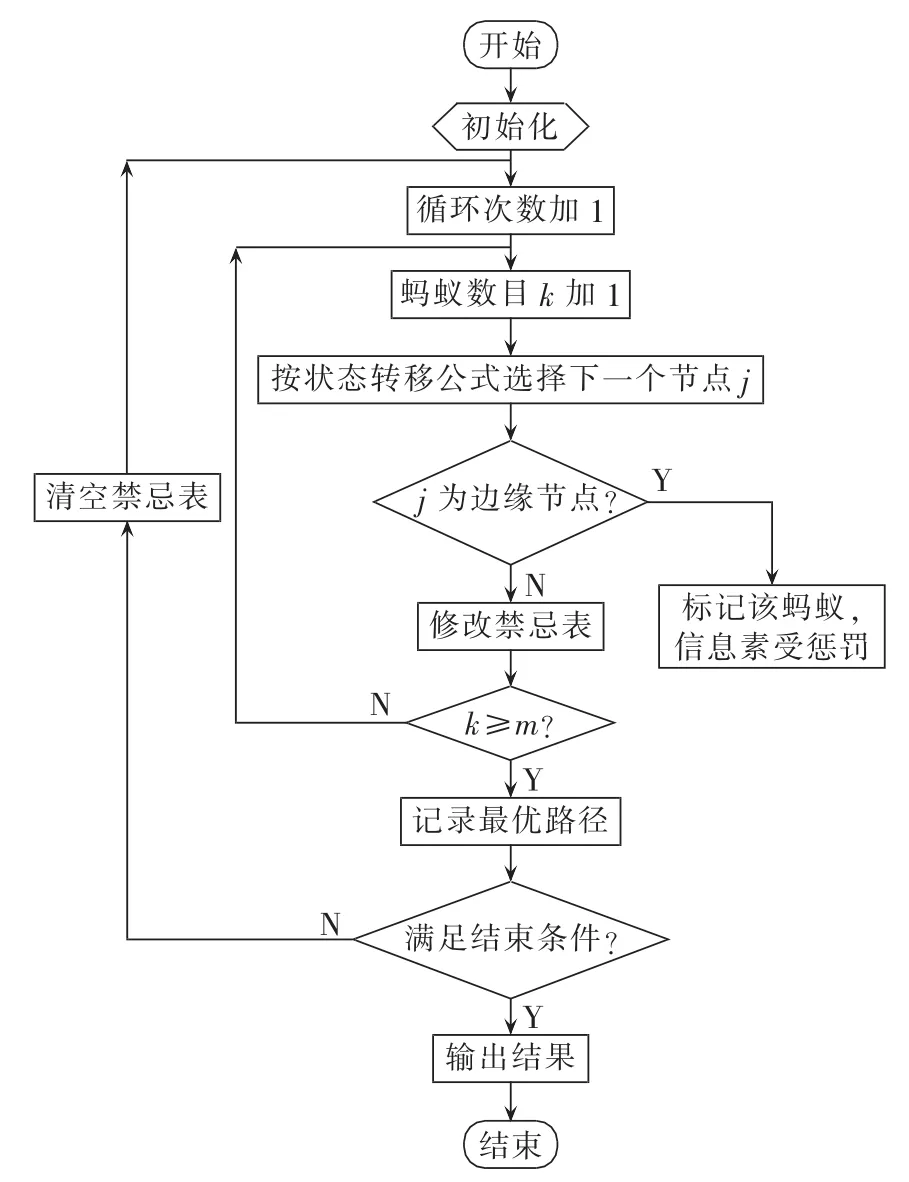
图3 改进的蚁群优化算法的流程图Fig.3 Flowchart of improved ant colony optimization algorithm

2.3 算法检验

利用图1所示道路网络拓扑，本文要求出从节点9到节点48之间的最短路径。选取：信息启发式因子 α=1.2，期望启发式因子 β=0.6，信息素挥发因子 ρ=0.5，蚂蚁数目 m=35，信息量 Q=1，迭代次数为100。仿真得到最短路径图如图4所示。

多次运用改进蚁群算法进行实验仿真，在第7次循环发现最优路径最优路径长度为 7.387 km。而应用基本蚁群算法在第31次收敛到局部最优，对应的最优路径长度为7.68 km，如图5所示。可以看出，改进的蚁群算法性能稳定，具有很好的全局收敛性能。

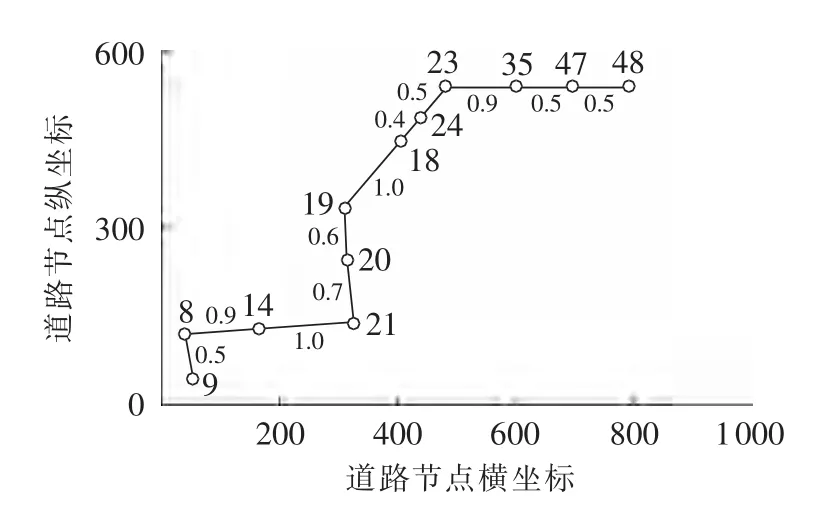
图4 最短路径仿真结果Fig.4 Simulative results of the shortest path

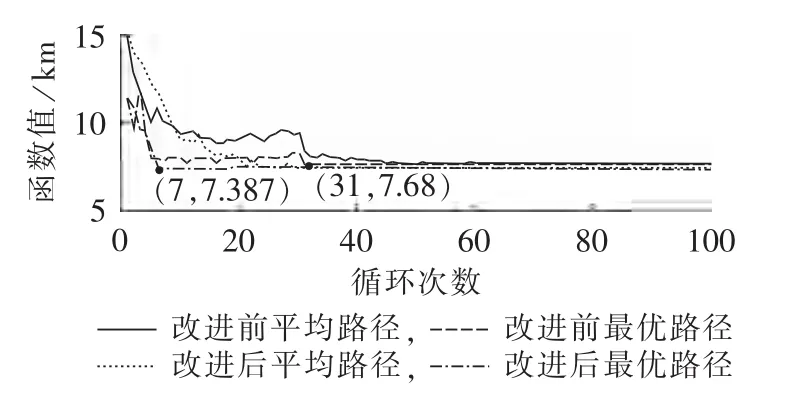
图5 传统蚁群算法与改进蚁群算法的性能比较Fig.5 Comparison of performance between traditional and improved ant colony optimization algorithms

通过以上仿真分析，可以发现本文算法在信息素更新时引入惩罚因子和在信息素初始化时加入方向引导，很大程度上减少了不必要的劣质解。信息素初始化时的差异指引着蚂蚁寻找较优解，可以有效地避免蚂蚁一开始盲目的寻优甚至误导后来的蚂蚁进行路径选择，明显加快搜索最优解的速度，提高解空间质量。同时，改进蚁群算法可以保证算法收敛到全局最优解。

3 模型求解

3.1 抢修系统模型求解

对于抢修车的动力电池配送最优路径选择，考虑道路等级、道路拥堵指数和实际道路长度等，在前面研究的基础上，假设事故点为节点1，其附近的配送站点为节点51，抢修车从配送站出发，载着动力电池到事故点对电动汽车进行换电操作。下面对抢修车的动力电池配送路径分不同的时间段进行仿真，使其更接近实际情况。由于早高峰与晚高峰的交通拥堵情况类似，白天与其他时间段类似，本文仅对早高峰（07∶00 — 10∶00）和白天（10∶00 — 16∶00）2 个时段仿真，仿真结果如图6、图7所示。

在早高峰时段，城中的拥堵指数是 6.6～7.1，处于中度拥堵状态；城东的拥堵指数是3.7，处于基本畅通状态；城西的拥堵指数是 4.1～5.4，处于轻度拥堵状态；城南的拥堵指数是 3.3～3.7，处于基本畅通状态；城北的拥堵指数为4.5，处于轻度拥堵状态；西湖风景区的拥堵指数为3.2～3.4，处于基本畅通状态。城区整体的拥堵指数较高，选择比较畅通的道路成为关键。仿真结果表明，最优路径的选择避开了较为拥堵的城中，除了事故地点城西比较拥堵外，最终选择的路段交通拥堵指数在3.7～4.5之间，处于基本畅通阶段。同时，在满足道路基本畅通的前提下，实验还较多地选择了快速路，避免选择支路，具体选择结果如表2所示。

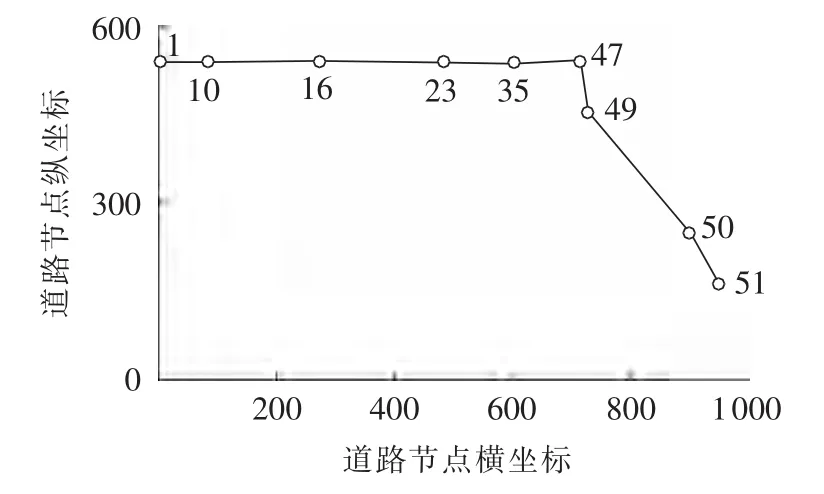
图6 早高峰07∶00—10∶00某时刻抢修车最优配送路径Fig.6 An optimal path of recovery vehicle during morning peak from 07∶00 to 10∶00

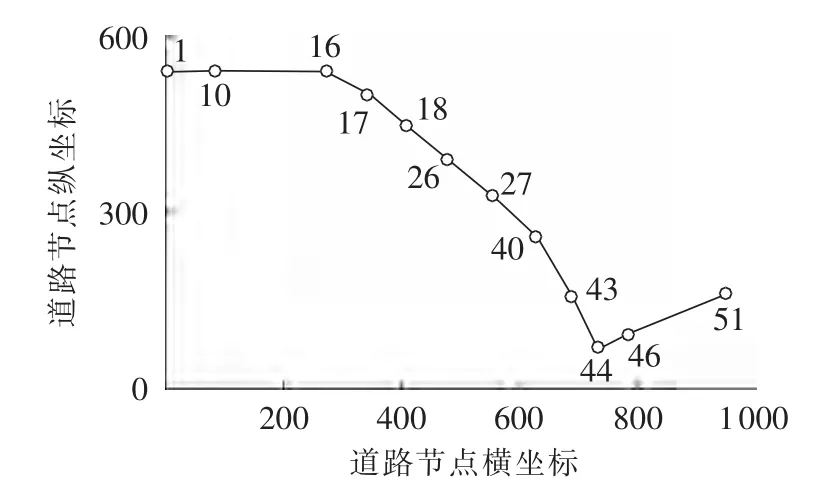
图7 白天10∶00—16∶00某时刻抢修车最优配送路径Fig.7 An optimal path of recovery vehicle during daytime from 10∶00 to 16∶00

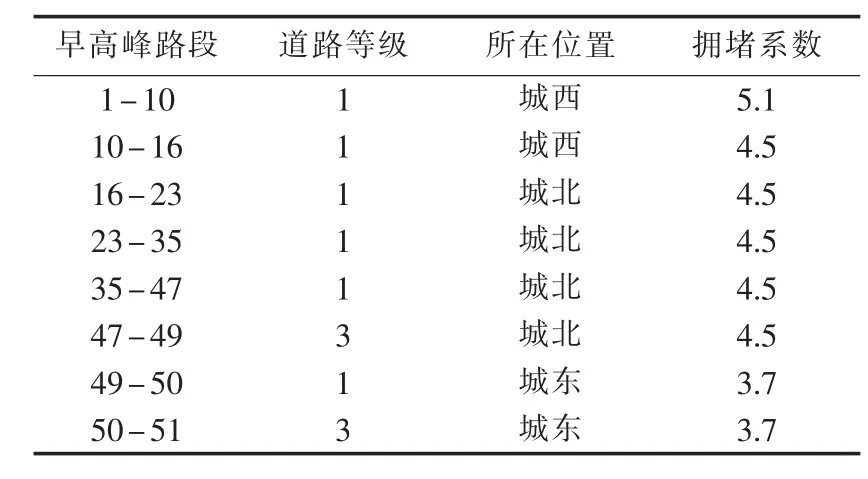
表2 早高峰07∶00—10∶00抢修车最优配送路径分析Table 2 Analysis of optimal path of recovery vehicle for morning peak from 07∶00 to 10∶00

10∶00— 16∶00 时段全城区的拥堵指数是 1.0 ～3.1，道路处于畅通或基本畅通状态。此时，决定选择最优路径的因素主要是道路的实际长度及道路等级。仿真结果表明，最优路径主要选择快速路，同时考虑路网实际分布状况和实际道路长度，选择次干路的道路，避免选择支路。选择结果如表3所示。

3.2 配送系统模型求解

杭州市区集中充电站、配送站的分布以及各配送站的电池需求量如图8所示。

配送车的载重为10 t，每日的最大行驶里程为100 km，路网抽象成完全连通图，并利用蚁群算法进行仿真。选取：信息启发式因子α=1，期望启发式因子 β=4，信息素挥发因子 ρ=0.5，蚂蚁数目 m=35，信息量Q=100，迭代次数为200，仿真得到电池配送路径图如图9所示。

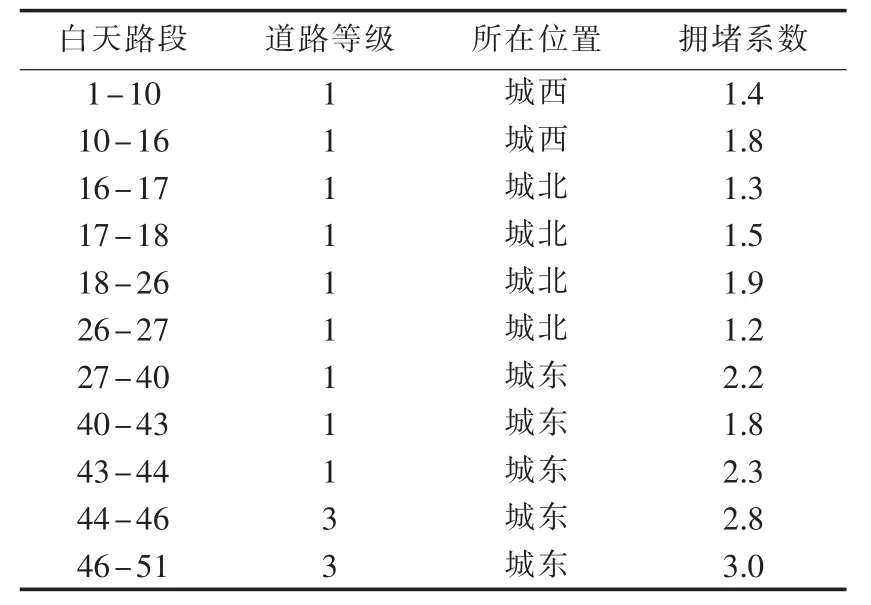
表3 白天10∶00—16∶00抢修车最优配送路径分析Table 3 Analysis of optimal path of recovery vehicle for daytime from 10∶00 to 16∶00

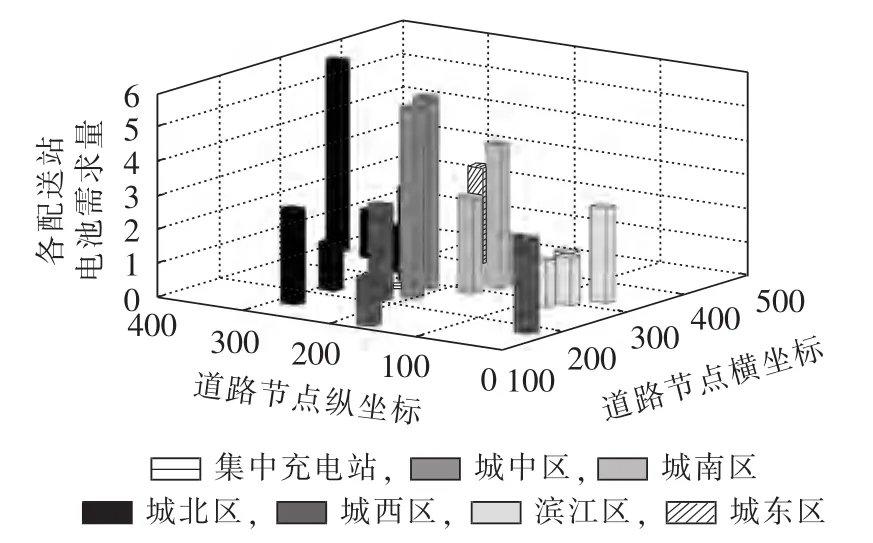
图8 杭州市配送站每日电池需求量Fig.8 Daily battery demand of distribution stations in Hangzhou

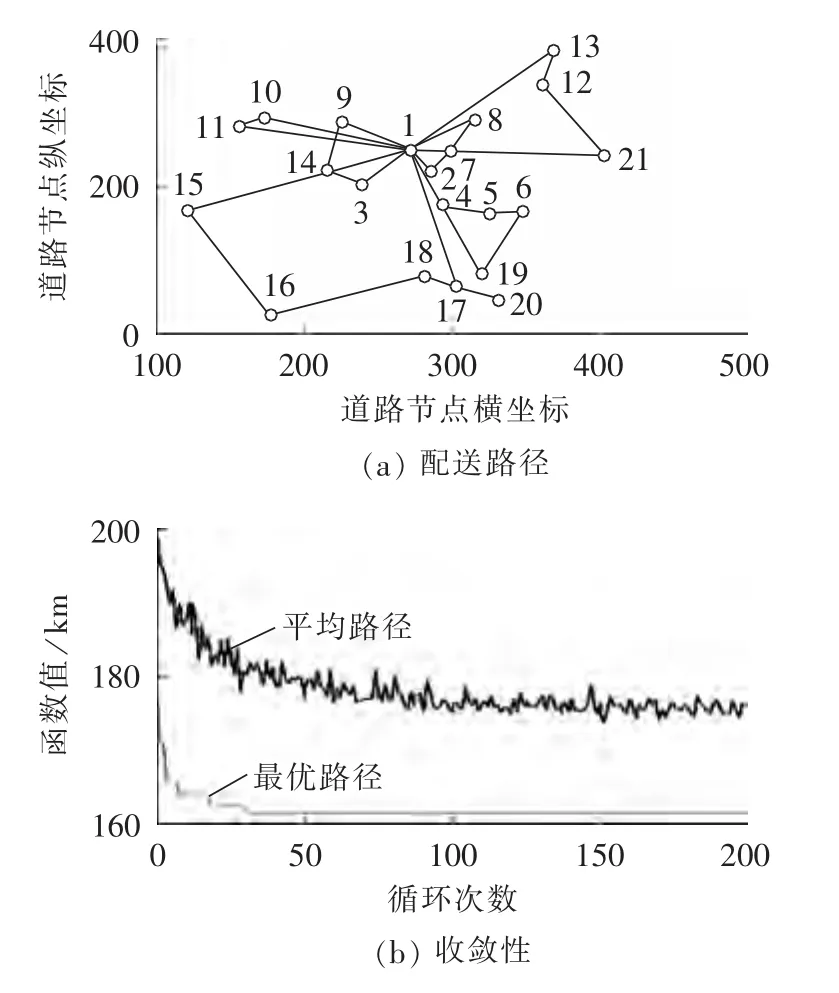
图9 配送车的配送路径及算法收敛情况Fig.9 Delivery paths of delivery vehicles and convergence of algorithm

由图9可以看出，选取载重为10 t的配送车辆，需要6辆，总的行驶里程为161.429 km。各车辆的配送路径分别为

4 结论

本文以杭州市充换电服务网络为背景，从电池配送的实际问题出发，分别建立电动汽车抢修路径规划和电池配送路径规划的数学模型。在抢修系统的数学模型中，以配送网络中实际道路的路径长度、交通堵塞系数和道路等级等效成的加权道路长度最小为目标函数，规划省时省路的最优路径；在配送系统的数学模型中，考虑车辆在道路上的等待时间，并考虑配送车的行驶里程限制和最大载重量限制，以配送成本最小为目标函数。然后根据路网的特点，对蚁群算法的相邻节点选择策略、信息素初始化策略以及信息素更新策略进行改进，提高算法的收敛速度。同时，为了避免下一次循环蚂蚁进入死路，引入惩罚因子，避免算法陷入局部最优。

仿真结果表明，改进的蚁群算法能够适应动态变化的路网结构，有效而快速地求得电池配送路径的最优解。本文的研究内容对电动汽车的发展具有很好的理论价值。