基于Blackman自卷积窗及三谱线插值修正的介质损失角计算方法

王永强，谢 军，律方成

（华北电力大学 输变电设备安全防御河北省重点实验室，河北 保定 071003）

0 引言

介质损失角是衡量电气设备绝缘性能的一个重要参数［1］，对介质损失角进行精确监测与计算能为电气设备故障诊断提供可靠依据，为电力系统安全稳定运行提供重要保障［2-3］。

正常情况下，介质损失角为一个很小的值，约为0.001～0.02rad［4］，实际测量中其真值常容易被误差所湮没。基于谐波分析理论（快速傅里叶变换（FFT）及其改进算法）的介质损失角计算方法由于算法易于实现、受直流及谐波分量的干扰小而成为了介质损失角计算的典型方法［5-10］，但由于电力系统频率常常发生波动，难以保证对待分析信号准确做到同步采样，使FFT存在频谱泄漏以及栅栏效应，其计算结果尤其是相位结果误差很大，难以直接用于介质损失角的计算［11］。基于 Blackman 窗［6］、Rife-Vencent窗［7］、Hanning 窗［8］、Kaiser 窗［9］、Nuttall 窗［10］等 加 窗插值FFT介质损失角计算方法相继被提出，通常这些方法是在信号加窗后利用目前应用较广的双谱线插值算法减小频谱泄漏及栅栏效应的影响，使介质损失角仿真计算结果绝对误差小于10-5rad［6-8］。

然而，采用传统加窗方法进行介质损失角计算时，计算量相对较大，且非同步采样时，传统窗函数抑制频谱泄漏的能力是有限的；仅采用双谱线插值会丢失与准确频谱相关的重要信息，甚至可能由于长程频谱泄漏的影响造成插值方向选择错误［12］，增大计算误差。为减少频谱泄漏对基波分析结果的影响，并提高插值法计算精度，进一步减小介质损失角的计算误差，本文提出了一种基于Blackman自卷积窗BSCW（Blackman Self-Convolution Window）及三谱线插值修正的介质损失角计算方法。在频率波动、介质损失角真值变化、谐波比例变化、白噪声影响等不同情况下，通过仿真实验，对比分析了运用本文所提方法、加Blackman自卷积窗结合双谱线插值法、加Blackman窗结合双谱线插值法这3种介质损失角计算方法的计算结果，同时讨论了采样频率对本文算法结果的影响；搭建介质损失角模拟测量实验平台，通过模拟实验验证本文所提方法的计算结果准确性。仿真与模拟实验结果表明，运用本文所提方法能够有效抑制频谱泄漏以及栅栏效应，介质损失角计算结果精度有较大提高。

1 Blackman自卷积窗及其频率特性

1.1 Blackman 自卷积窗定义

文献［13］对矩形窗进行自卷积运算构造矩形自卷积窗从而提升了窗函数旁瓣性能。由于原始矩形窗旁瓣性能较差，进行自卷积运算旁瓣性能提升有限，为了进一步提高旁瓣性能，参照文献［13］方法，本文采用旁瓣性能较好且结构相对简单的Blackman窗进行自卷积运算，构造Blackman自卷积窗。

长度为N的Blackman窗wB（n）可表示为：

其中，n=0，1，…，N-1。

由自卷积性质，长度为N的Blackman窗进行P阶自卷积后，所得新序列长度为NP-（P-1），在该卷积序列末尾补零，可得P阶Blackman自卷积窗wBP（n），即：

长度为N的Blackman窗序列经P阶自卷积并补零后，所得P阶Blackman自卷积窗长度NP=NP。

1.2 Blackman自卷积窗频率特性

根据离散傅里叶变换，长度为N的Blackman窗的频谱函数为：

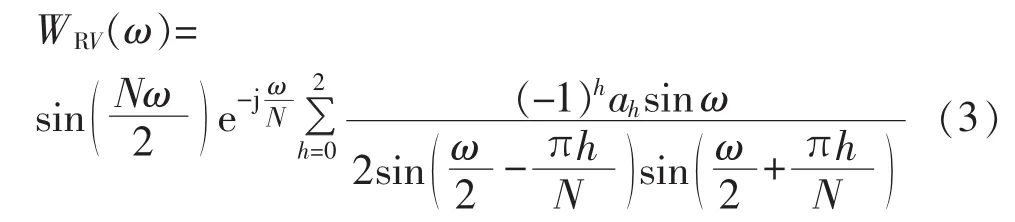
其中，ω为归一化角频率；ah为Blackman窗各项系数，a0=0.42，a1=0.5，a2=0.08。

由卷积定理，信号在时域内卷积等于其在频域内乘积，故P阶Blackman自卷积窗频谱函数为：

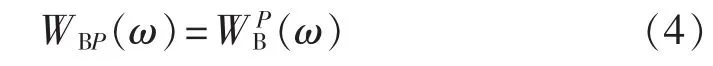
根据1.1节中的分析，长度为N的Blackman窗P阶自卷积后，新窗的长度为NP=NP，对式（4）离散化，即 ω=2 kπ/NP（k=0，1，…，NP-1）。 P 阶Blackman自卷积窗离散频谱函数为：

当 k=（3+τ）NP/N（τ=0，1，…，N-4）时，上式成立。

由式（6），当τ=0时，k为中心频点右侧首个过零点，此时k=3P，故中心频点与右侧首个频率过零点之间的距离为6Pπ/NP，由离散傅里叶变换基本性质，频率分布关于中心频点对称。故主瓣宽度为：

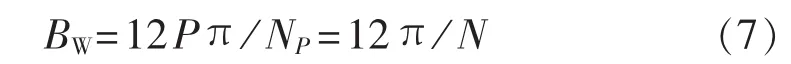
由式（7）可知，P阶Blackman自卷积窗的主瓣宽度和原Blackman窗主瓣宽度相等。

由式（6），τ=1时，k为中心频点右侧第2个过零点，故 k=（3+0.5）NP/N=3.5P 时，具有最大旁瓣值，则Blackman自卷积窗的旁瓣峰值电平B（单位为dB）为：

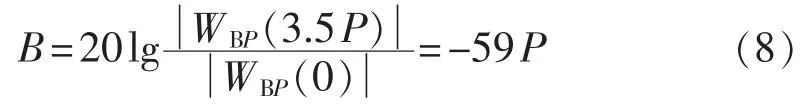
Blackman自卷积窗的旁瓣衰减速率V（dB/倍频程）定义为倍频程的旁瓣值之比的分贝数：

由式（8）、（9）知，随着卷积阶数的提高，旁瓣峰值迅速减小，旁瓣衰减速率迅速增大。P=4时，旁瓣峰值电平达-236dB，旁瓣衰减速率为72dB/倍频程。由此可见，Blackman自卷积窗具有非常良好的旁瓣性能，能够有效抑制频谱泄漏效应。

2 三谱线插值理论

待测信号经采样频率为fs的数据采集系统后，被长度为NP的P阶Blackman自卷积窗截断为序列xW（n），对此序列进行离散傅里叶变换，考虑到本文所提Blackman自卷积窗优越的旁瓣性能，负频率分量的频谱泄漏影响作用可忽略不计［13］，忽略其余谐波产生的频谱泄漏影响，基波频谱函数为：

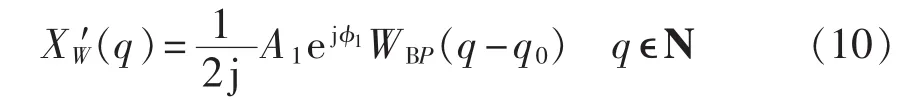
其中，A1为基波幅值；φ1为基波相位；q0为基波谱线在离散谱线中的位置，并有q0=fs/f0，f0为基波频率。

非同步采样时，q0为非整数，其不与任一离散谱线q重合，会有一定频率偏移量。直接通过某离散谱线q计算基波各参量尤其是初相位会有较大误差。常用的双谱线插值法是利用q0附近两幅值较大谱线进行插值计算得到频率偏移量近似值［6-8］。然而，最大幅值谱线及其左右紧邻谱线往往均具有较大幅值，且这些谱线均主要是由基波频谱泄漏产生的，含有丰富的基波相关信息，只用两幅值较大谱线进行插值运算势必会造成基波信息量的丢失［14］；且仅用两幅值较大谱线插值运算，当这两谱线幅值几乎相等时，由于负频率分量长程泄漏作用可能会使插值方向选择发生错误，严重影响校正精度［12］。 文献［14］提出利用最大幅值谱线及其左右紧邻谱线这3根幅值较大谱线用于插值计算即三谱线插值频谱校正方法避免上述影响，提高频谱校正精度。

设幅值最大谱线为q2，则其左右幅值较大谱线分别为q1和q2，且有q1=q2-1、q3=q2+1。对应的谱线幅值分别为由于 q0-q2є［-0.5，0.5］，引入参数 λ，并令 λ=q0-q2，则 λє［-0.5，0.5］。

由于 f（λ）=-f（-λ），即 β=f（λ）为奇函数，故其反函数λ=f-1（β）仅有奇次幂项，可由最小二乘法对λ=f-1（β）进行拟合，进而由 β 求得［15］。 考虑到算法计算精度与复杂程度，逼近次数一般不超过7次［14］，对于4阶Blackman自卷积窗，其三谱线插值多项式拟合函数为：

由于幅值最大谱线最接近基波准确谱线，且噪声对其影响效果最小，用其值进行修正，结果精度较高，故应用q2谱线进行修正。由λ＝q0-q2，有：

分别对电流与电压信号进行分析，可求得电流与电压基波信号的相位角分别为φi1、φu1，则介质损失角为：

3 介质损失角仿真计算与结果分析

3.1 仿真模型

容性设备可采用电容串联电阻或电容并联电阻这2种等效电路进行模拟，如图1所示。

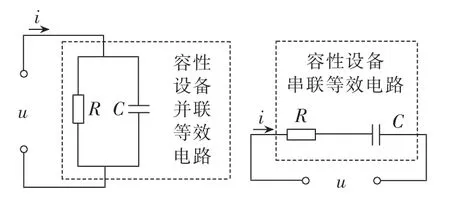
图1 容性设备等效电路Fig.1 Equivalent circuit of capacitive equipment

设R、C分别为等效电路电阻及电容值，则并联等效电路及串联等效电路介质损失角计算公式分别如式（15）、（16）所示。

本节采用串联等效电路等效容性设备，其中电容值 C=591.02 pF，电阻值 R=22.67 kΩ，基波频率为50 Hz时，介质损失角为0.004209 rad。电压信号由基波、3次谐波和5次谐波组成，其表达式为：因此，流过该容性设备的电流信号表达式为：i（t）=u（t） /Z，Z 为该容性设备等效电路阻抗值。

为了验证本文所提介质损失角测量算法效果，采用了加Blackman自卷积窗结合三谱线插值法、加Blackman自卷积窗结合双谱线插值法、加Blackman窗结合双谱线插值法这3种基于FFT的介质损失角计算方法，仿真分析在不同情况下介质损失角的计算结果。双谱线插值法采用文献［6］中方法。其中，Blackman自卷积窗由原始长度为64的Blackman窗构建4阶自卷积窗得到，即自卷积窗长度为256，信号采样长度为256，采样频率为2.25 kHz；对于普通Blackman窗，窗函数长度为512，信号采样长度为512，采样频率为 2.25 kHz。

3.2 基波频率波动对介质损失角计算结果的影响

电力系统基波频率波动情况时有发生，为了验证基波频率波动对本文算法结果的影响，结合3.1节中仿真模型，基波频率在49.6～50.4Hz范围变化时，3种介质损失角计算方法计算结果如表1所示。

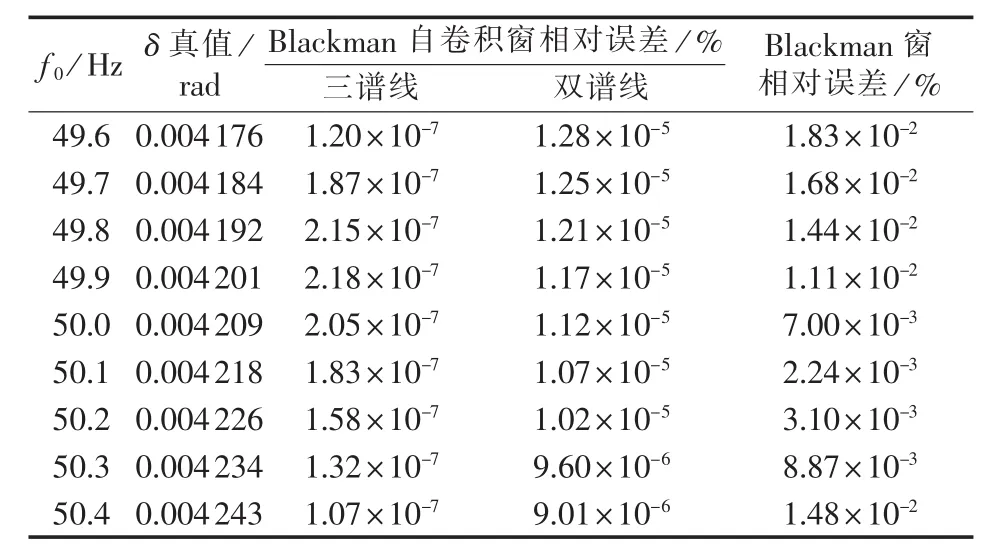
表1 基波频率波动对介质损失角计算结果的影响Table 1 Influence of fundamental frequency on DLA calculation

由表1可知，系统基波频率波动时，相比普通Blackman窗，Blackman自卷积窗的介质损失角计算误差更小；三谱线插值比双谱线插值计算精度提高了大约2个数量级；基于本文方法的介质损失角计算精度明显提高，在正常频率波动范围（49.8～50.2 Hz）内，只需较少采样数据和较小采样频率就可实现介质损失角的高精度计算，且相对误差小于2.5×10-7%。

3.3 介质损失角真值变化对计算结果的影响

介质损失角通常是一个很小的值，其真值越小，测量结果越容易被误差所湮没。为了分析介质损失角真值变化对本文算法的影响，通过仿真模型中电阻值R的改变实现介质损失角真值的变化。基波频率为50.1 Hz时，不同介质损失角真值下，3种计算方法的介质损失角计算结果如表2所示。

由表2可知，3种介质损失角计算方法均能有效跟踪介质损失角真值的变化；介质损失角真值相同时，加普通Blackman窗的双谱线插值法计算介质损失角误差最大，基于本文方法的介质损失角计算精度最高；介质损失角真值在 0.001～0.02 rad 范围内时，利用本文方法计算的介质损失角相对误差小于1×10-6%。

3.4 谐波比例变化对介质损失角计算结果影响

由于频谱泄漏的作用，谐波会对基波的计算结果产生影响，谐波比例变化将直接影响到介质损失角的测量结果。在基波频率为49.9 Hz时，3次谐波注入比例从0变化至10%时，各方法介质损失角计算结果如表3所示。

表2 介质损失角真值对测量结果的影响Table 2 Influence of DLA true value on DLA calculation

表3 谐波比例对介质损耗角计算结果的影响Table 3 Influence of harmonic ratio on DLA calculation

由表3结果可知，当3次谐波注入比例发生变化时，采用相同插值方法，基于Blackman自卷积窗的介质损失角计算精度明显高于普通Blackman窗；加Blackman自卷积窗时，三谱线插值算法的计算精度比双谱线插值法的计算精度高大约2个数量级。基于Blackman自卷积窗及三谱线插值法的介质损失角计算方法能有效克服谐波比例变化对计算结果的影响。

3.5 白噪声对介质损失角计算结果的影响

电气设备介质损失角及其正切测试现场有大量的电磁噪声。在白噪声环境下，介质损失角真值易被噪声所湮没。基波频率设置为50 Hz，不同信噪比下，各方法介质损失角的绝对误差e如图2所示。

图2 白噪声对介质损失角计算结果的影响Fig.2 Influence of white noise on DLA calculation

对比分析3种方法的计算结果可知，白噪声对本文算法的影响最小，采用本文介绍算法，可有效避免噪声对介质损失角计算精度的影响。当信噪比大于60 dB时，本文方法介质损失角计算结果绝对误差小于10-5rad，其准确度比采用双谱线Blackman自卷积窗介质损失角计算方法高1～2个数量级。

3.6 采样频率变化对本文算法介质损失角计算结果影响

为了研究采样频率对本文算法精度的影响，基波频率设置为 49.8 Hz，改变采样频率，运用 3.1 节中介绍的仿真模型对本文算法进行仿真计算，其结果如表4所示。

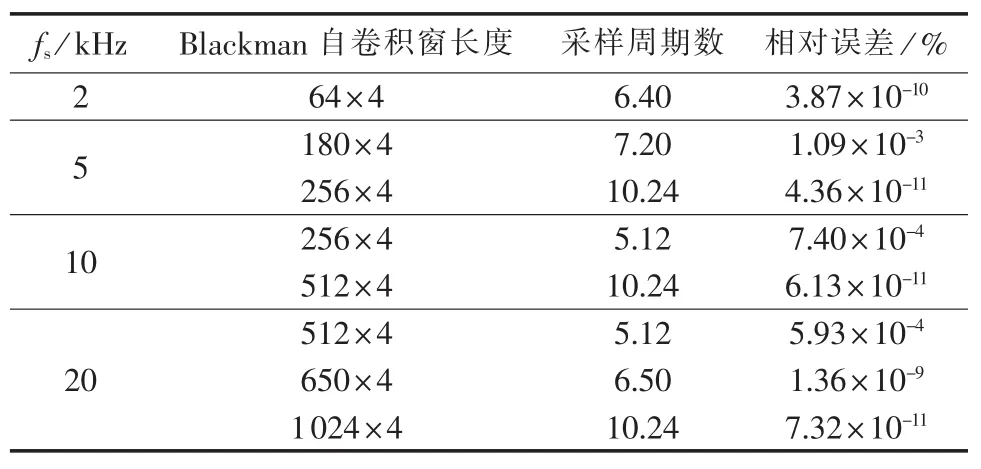
表4 采样频率变化对介质损失角计算结果的影响Table 4 Influence of sampling frequency on DLA calculation

表4 结果表明，采样数据过短时，介质损失角计算结果误差会有所增加，这主要是因为采样数据较短时，负频率部分频谱泄漏效应对基波的影响会加大，影响文中三谱线校正插值公式的适用条件，适当增加采样数据的长度可保证基波频点距离ω=0较远，可有效避免负频率部分频谱泄漏影响［12］，保证介质损失角的计算精度。因此采样频率变化时，本文算法能满足介质损失角计算精度的要求。

4 实验室模拟实验验证

由于现场实际容性设备介质损失角受温度、湿度等因素的综合影响，且西林电桥易受现场电磁场等干扰，难以直接得出介质损失角准确值，无法验证本文算法的计算结果精度。为了进一步验证本文所提算法的准确性和有效性，本文在实验室进行了介质损失角模拟测量实验，实验接线图如图3所示。

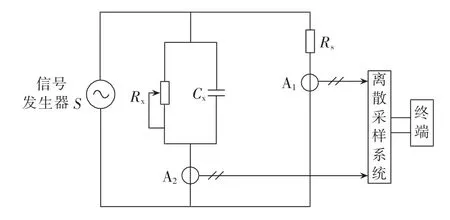
图3 实验接线Fig.3 Schematic diagram of experimental wiring

信号发生器用于产生固定频率的正弦交流信号；采用并联等效电路模拟容性设备［16］，其中，Rs为采样电阻，等效电容Cx为4个标称值为22 μF的电容并联而成，电阻Rx是1～15 kΩ的可变电阻，通过调节图3中的旋钮实现电阻的变化，进而模拟容性设备不同介质损失角真值。A1、A2为BCT-2型穿心式微电流传感器，该传感器基于Rogowski线圈原理，同时采用零磁通补偿技术减小误差，使测量电流在工频附近时，相角误差可以忽略。其中A1同采样电阻配合，用于测定试品两端电压信号，A2用于测定试品泄漏电流信号；电压信号、电流信号经PCI-9812数据采集卡采集并保存送入计算机进行计算；经信号发生器产生的电源信号为50.1Hz，采样精度为12位，采样频率设置为1 MHz，为非同步采样。

为了便于验证本文介绍介质损失角计算方法计算结果的准确性，实验前用DMM4050型高精度数字万用表测出 Cx、Rx的实际值，由式（15）计算出介质损失角实际值。

运用本文算法对信号进行分析并计算出介质损失角。表5为不同介质损失角真值下，运用本文方法的介质损失角测量结果。

表5 模拟实验介质损失角测量结果Table 5 Measured DLAs by analogue experiment

由表5结果，考虑到实验干扰、采样精度等对结果影响后，运用本文方法得到的介质损失角计算结果仍然保持较高精度，验证了本文方法的有效性与准确性。

5 结论

本文研究了Blackman自卷积窗的频率特性，给出了Blackman自卷积窗旁瓣峰值电平及旁瓣衰减速率与自卷积阶数的关系；在分析加窗信号离散频谱基础上，提出基于三谱线插值的FFT修正方法。结合上述分析，提出了一种基于Blackman自卷积窗和三谱线插值法的介质损失角测量方法。在不同情况下，对比分析了本文所提算法与加普通Blackman窗及Blackman自卷积窗的双谱线插值法的介质损失角计算结果，给出了采样频率对本文算法结果的影响关系，并通过模拟实验验证了本文所提方法计算结果的有效性与准确性。本文结论如下：

a.Blackman自卷积窗旁瓣性能优越，能有效抑制频谱泄漏，提高介质损失角计算精度；

b.相比双谱线插值法，三谱线插值法可进一步提高介质损失角计算精度，且加同样Blackman自卷积窗时，精度高约2个数量级；

c.本文方法计算结果精度高，为容性设备介质损失角在线监测提供了一种潜在的高精度算法。