智能电网用空间电能集能转换器
邹 亮 ,黄金鑫 ,刘梦琦 ,赵 彤 ,张 黎
(1.山东大学 电气工程学院,山东 济南 250061;2.国网技术学院,山东 济南 250002)
0 引言
智能电网是未来电力工业的发展方向[1],其对传感和测量技术提出了更高要求,这也导致无线传感器在智能电网中占据了重要地位。但是无线传感器能量的供给问题却未得到有效解决[2-3],为此尝试采用的增加电池能量密度、新的能量传输方法[4]等,因安全性及能耗大等缺点而搁置。而收集周围环境中的能量[5-9](太阳能、振动能、热能、电磁能等)并转换为电能的自供能技术可以有效解决无线传感器网络的能量供给问题。
由于变电站特殊的空间布局及环境要求,基于太阳能的自供能技术受到限制;出于绝缘和安全考虑,振动能量收集装置也不可直接外挂于电气设备上;而众多新型自供能技术(如热能自供能和声能自供能)因其能量源太微弱无法达到要求。因此,针对变电站的特殊电磁环境,科研人员开始研究基于空间电磁能的无线传感器自供能技术[10]。
现代化高压变电站或输电线路周围蕴含丰富的电磁能量。实测数据表明,500 kV高压变电站内的工频电场强度可达18 kV/m,变电站内的电场能量非常丰富[10]。因此,为将高压变电站中的电场能转换为可以为无线传感器网络供能的电能,本文采用电容式集能转换器来实现该功能。电容式集能转换器主要包括2个部分:集能拓扑和调理电路。集能拓扑的作用是实现能量由空间强电场能到可供无线传感器网络供能电能之间的转换。调理电路的作用是将收集到的无规则脉冲电流或脉动电压进行调理,使经调理电路处理过的电能可直接为无线传感器所使用。本文的研究正是基于两者展开的。
1 电容集能拓扑性能分析
外电场条件下的电能转换能力是由电容集能拓扑决定的。电容集能拓扑的典型结构为平板型,但其只对垂直其轴线方向的电场集能效果较好。在变电站复杂电场环境下,球型集能拓扑更适于跟踪收集各方向的电场分量,并且球型拓扑近似封闭的金属面还为内置电路提供了电磁屏蔽,可避免尖端放电现象[11],本节将对其进行数学建模。
1.1 集能拓扑数学建模
由于自供能装置收集工频电场能量时,主要工作在低频电场下,且电容集能拓扑的尺寸远小于波长,因此可用准静态场的方法来分析。设球壳半径为R,电势为 u,空间任意一点 P(r,θ,φ)电势满足拉普拉斯方程Δ2u=0,其中,θ为P点与球心的连线与z轴的夹角,φ为P点与球心的连线映射在xy平面上所形成的线段与x轴的夹角。在球坐标系下,因φ满足旋转对称性,u与φ无关,故拉普拉斯方程在球坐标系下的展开式[12]可简化为:

采用分离变量法,设 u(r,θ)=X(r)Y(θ),X 和 Y分别为关于r和θ的函数,代入并整理得:

其中,n(n+1)为分离变量法时产生的常数,满足在有限区域内电势处处有限且有解。 令 x=cos θ、y(x)=Y(θ),方程(2)变为:
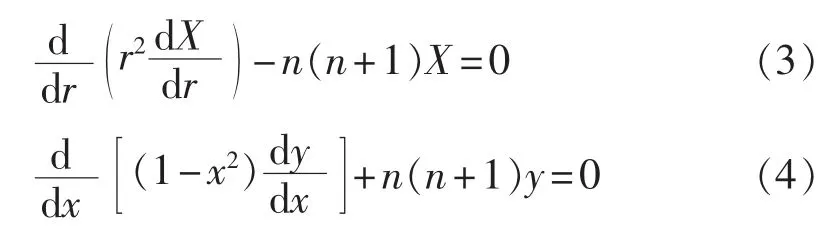
方程(3)为欧拉方程,其通解为:

其中,A和B为待定常数,可通过边界条件求取。
方程(4)的解是一个勒让德多项式:

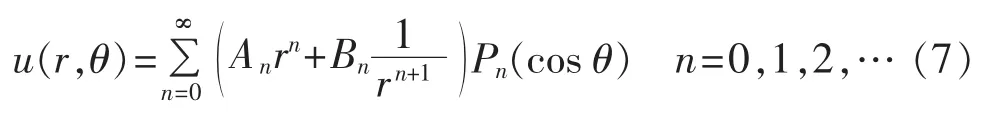
则电势的通解可表示为:下面在2种边界条件情况下求解球型拓扑电容以及输出电压的表达式。
a.设球型拓扑的上、下金属半球的电位分别为U和-U,外加电场为0,无穷远处电势为0,根据这3条边界条件可确定式(7)中的待定系数分别为:

球型拓扑表面电场强度为:
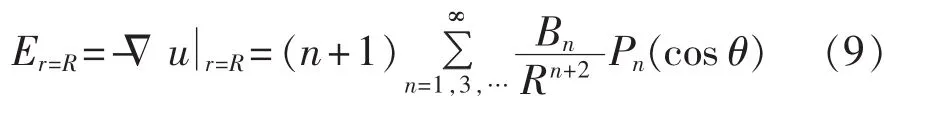
球型拓扑极板上的电荷为:
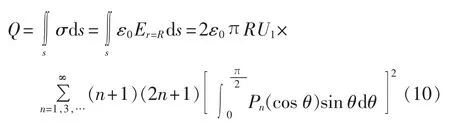
则球型拓扑的电容为:
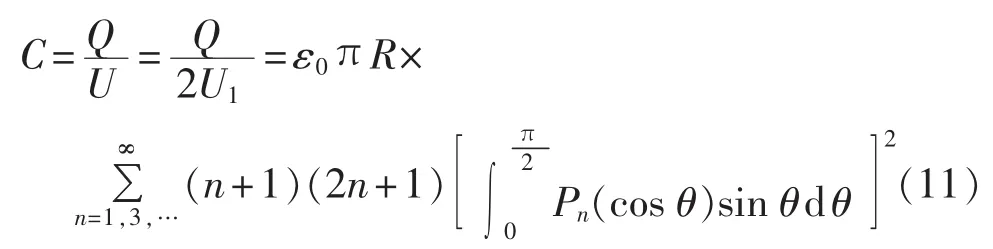
其中,ε0为真空介电常数。
b.当外加电场E0为均匀电场时,边界条件为Er=∞=E0,则:

常数D可通过适当的零电势参考点选择而取值为0,再利用勒让德多项式的正交关系可得:
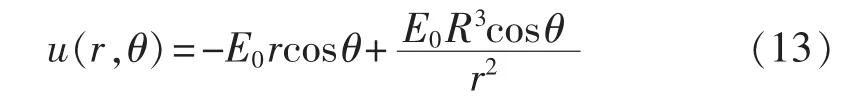
式(13)中等号右侧第1项是原来匀强电场产生的电势,第2项是因导体球受到电场的作用而类似极化为一个偶极矩为E0R3的偶极子所产生的电势。
同理,球壳电极上的电荷量为:

则球型拓扑输出电压的数学表达式为:

式(15)可推广到外界均匀场强E0与集能拓扑z轴成一定角度δ的普遍形式。当外电场与集能拓扑z轴垂直时,由对称性可知上下两半球极板等电势,即无输出电压,因此球型集能拓扑对垂直于z轴的电场分量无收集作用。最终,球型集能拓扑的输出电压与球壳半径和外电场的关系为:
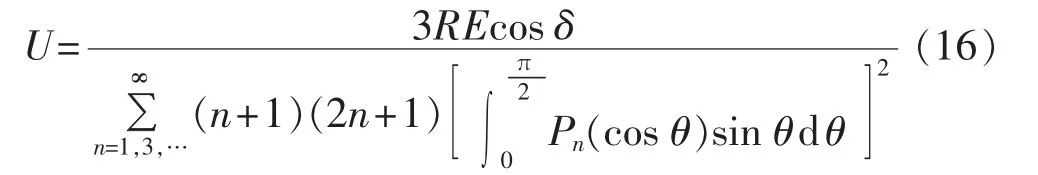
其中,δ为任意方向的均匀场强与集能拓扑z轴的夹角。
由式(16)可看出,球型集能拓扑的输出电压由球半径和外界场强的大小及方向共同决定。以集能拓扑输出电压最大为优化目标时,应综合考虑球半径和外界电场因素;当外界电场一定时,球半径越大,输出电压越大,优化约束条件则变为集能拓扑的体积限制。
在实际应用中,采用球冠型集能拓扑结构,该种结构上极板保持弧形,下极板设计为平板形状,这主要是由于球型结构接地连接的不稳定以及弧形下极板电势近于地表电势。如图1所示的球冠型集能拓扑可保持球型拓扑适应复杂电场环境的优点,其电容和电势表达式的推导过程与上述类似,不再赘述。

图1 球冠型集能拓扑结构Fig.1 Structure of sphericalcap energy scavenging topology
1.2 集能拓扑空载实验
本文采用的自供能系统实验平台主要由电场发生单元、轻型高压试验变压器、示波器以及分压器等单元组成,通过该实验平台可以验证集能拓扑的实际特性。其中电场发生单元由面积为1 m2的两平行金属极板组成,用高度为1 m的绝缘支柱支撑,通过轻型高压试验变压器连接50 Hz交流电网。因为本节主要针对集能拓扑的能量收集效果以及参数变化对集能效果的影响,所以空载实验在较低电压下进行。
制作拓扑和结构参数各不相同的集能单元试样。将不同拓扑结构和参数的试样置于电场发生单元中,以示波器观察其空载波形。调节变压器,使电场发生单元两端电压的峰值在50~300 V之间变化,观察集能拓扑两端的电压变化趋势。假设电场方向与集能拓扑中轴线夹角为δ,在平板和球冠半径以及高度相同且δ=0°时,球冠型拓扑的集能电压更高,如图2(a)所示,图中输入和输出电压均为电压峰峰值。针对球冠型集能拓扑,改变其半径R和高度d,观察集能电压的变化,如图2(b)、(c)所示,可知增大球冠的半径R和高度d均能增大集能拓扑的输出电压。为研究电场方向变化对集能拓扑集能效果的影响,实验中保持半径R和高度d不变,改变δ,观察集能拓扑的输出电压特性。由于实验中的测量误差以及电场发生单元的电场畸变,当增大δ时,平板型集能拓扑的集能效果有一定的降低,如图2(d)所示,但球冠型拓扑没有变化。
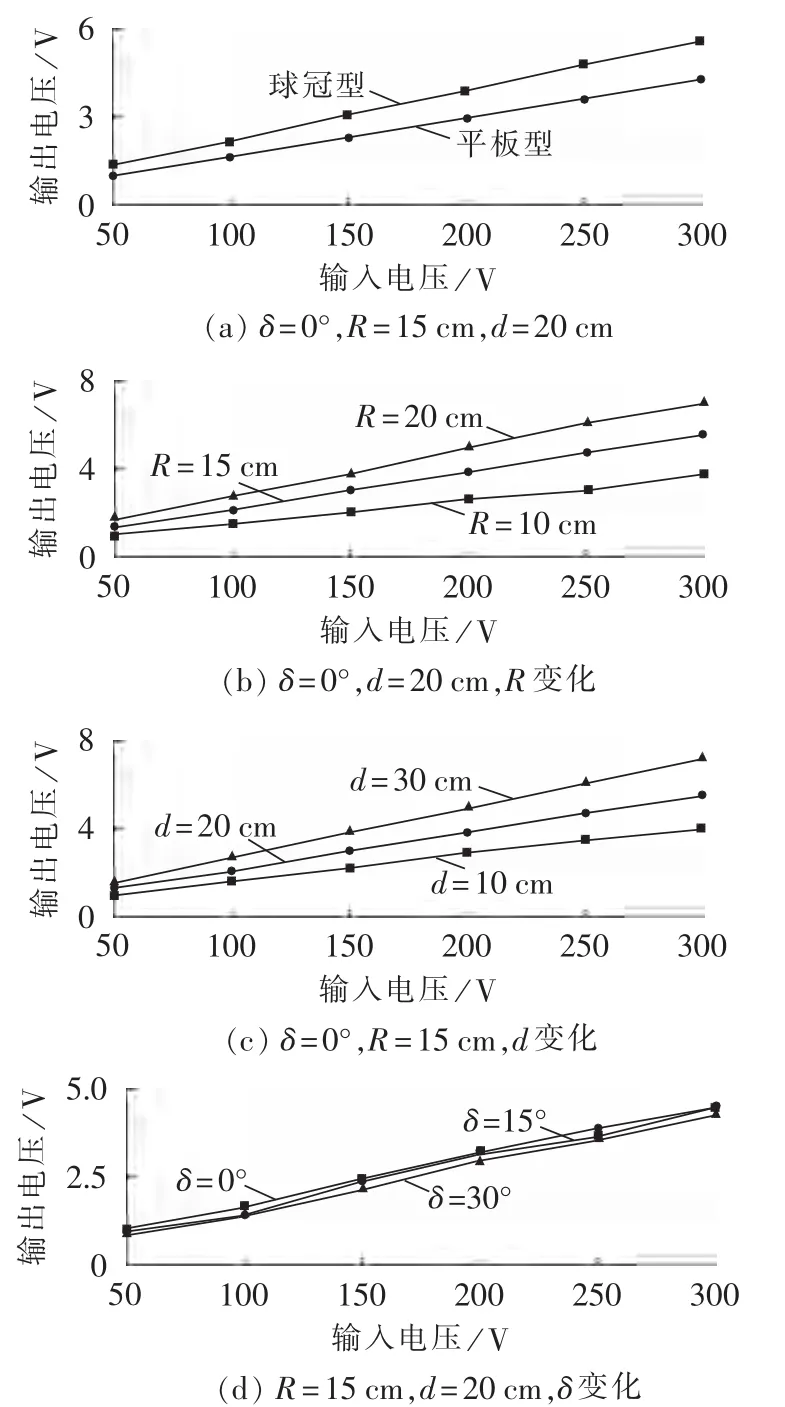
图2 2种集能拓扑的输出特性对比Fig.2 Comparison of output characteristics between two energy scavenging topology types
为更直观地对比2种拓扑的集能效果,本文选择对比平板型拓扑与球冠型拓扑的2个基本性能指标:转换器的输出电压U与电容储能Wc。转化器输出电压U可直观反映集能效果;电容储能Wc直接决定了拓扑的集能上限。当电场方向与集能拓扑中轴线夹角δ=0°时,取半径R同为15 cm的平板型和球冠型转换器,极板高度d调节为20 cm,调节变压器,使电场发生单元的输出电压为300 V,2种拓扑的实验结果如表1所示。
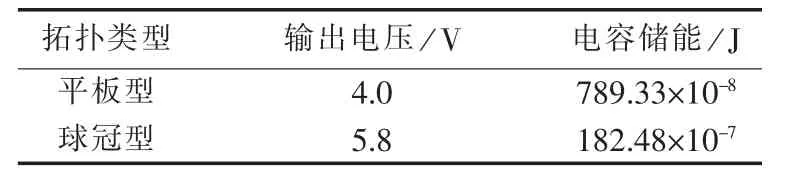
表1 2种集能拓扑参数对比Table 1 Comparison of parameters between two energy scavenging topology types
实验与仿真结果表明,在相同半径和高度的条件下,球冠型拓扑的集能效果要优于平板型拓扑。球冠型拓扑的半径、高度以及电场的强度对集能效果影响显著,且近似成正比关系。由于测量误差、电场发生单元的电场畸变以及实验中集能拓扑角度变化限制等,实验中δ在30°以下变化时,角度变化因素对球冠型拓扑的集能效果影响不明显。
2 调理单元拓扑设计与仿真
因外部电场的不断变化以及传感器负载在发射和休眠工作状态的转换所导致的等效阻抗的变化都将引起电路输出电压及功率的波动,加之集能拓扑能量收集的断续性和波动性,必须设计可实现整流、斩波、存储和稳压等功能为一体的调理电路。调理电路的主体是稳压子系统、整流子系统和存储子系统。
2.1 调理单元拓扑设计
图3所示为满足无线传感器功能要求所设计的调理电路拓扑。该拓扑中,先采用简单的单相整流桥将集能拓扑两端电压转换为近似的直流,其后接存储电容将收集的能量暂时存储起来,同时该能量也可为后端控制电路提供工作电压。为达到稳压目的,调理拓扑中采用了Buck电路。当外电场变化或负载变化时,由Rx和Ry组成的反馈回路可将输出电压波动经补偿网络传递给PWM器,后者通过调制的脉宽信号控制开关VT的开通时间,最终达到稳压的目的。

图3 调理电路拓扑Fig.3 Topology of conditioning circuit
2.2 调理拓扑主电路数学模型
为研究调理拓扑主电路的输出电压特性,经桥式整流和电容滤波后,后续电路可近似等效为DC/DC变换电路。为获得调理电路直流稳态时的输出电压特性,本文应用开关周期平均值法[13-14],建立了调理电路的大信号模型:

其中,us(t)为电容 Cs两端的电压;uo(t)为输出电压;i(t)为电感电流;〈x(t)〉Ts表示一个开关周期 Ts中,变量 x(t)的平均值;d(t)为开关占空比。
设电路稳定在某一静态工作点,则其稳态时的占空比 d(t)=D,电感电流为 I、输出电压为 Us、输出电压的稳态值为Uo。根据电感电压的伏秒平衡原理和电容电荷的平衡原理[14],电感电压的平均值和电容电流的平均值都等于零。将占空比以及各变量的稳态值分别代入上述大信号模型,可推导得到各稳态量之间的关系式:

其中,Us、Uo分别为电路处在静态工作点(电路处在直流工作状态下)时的输出电压和稳态电压。
经整理:

由调理电路的大信号建模,可得到直流稳态时各变量之间的关系。从式(19)可看出,输出电压的直流稳态值与输入电压和占空比的大小有关。占空比越大,输出直流稳态电压值也越大,通过合理调节高频开关的占空比,可使得电路输出电压在数值上满足无线智能传感器的供能要求。
当负载和输入电压变化时,输出电压将会产生较大波动,因此,为研究扰动对电路输出电压的影响,有必要建立调理电路的动态小信号模型。如果电感电流、输入电压、输出电压和占空比在直流工作点附近作小扰动,并以的扰动量,将扰动量代入式(17)中,消去直流项并忽略二阶交流项,可得如下的交流小信号模型:

对上式进行拉普拉斯变换并整理可得:

2.3 外电场变化下的调理主电路特性
因外部电场可能不断变化,集能拓扑两端的电压会随外电场的变化而波动,输入电压的大幅波动将会使得调理主电路产生丰富的非线性现象,即各种类型的分岔和混沌[15],这将直接影响调理主电路的稳定性和可靠性。
根据式(17),分别单独列写VT导通和关断时的状态方程,并对状态方程进行拉普拉斯变换,可分别得到VT导通和关断时的方程为:

根据式(22)和(23),搭建调理主电路的 MATLAB/Simulink仿真模型如图4所示。在该仿真模型中,设定主电路参数为:Us=20 V(等效输入电压),L=1mH,C=500 μF,R=1 kΩ,T=10 μs,Rx=15 kΩ,Ry=15 kΩ,仿真输出为I-U关系曲线。

图4 Simulink仿真模型Fig.4 Simulation model by Simulink
通过仿真发现,调理主电路的有效输入电压范围为5~30 V,当等效输入电压Us低于5 V或超过30 V时,电路工作在不稳定的周期状态,容易产生混沌,影响主电路工作的稳定性。因此,为保证调理主电路输出电压的稳定性,一方面优化集能拓扑结构以尽量降低外电场变化对集能电压的影响,另一方面调理电路应增加稳压反馈回路,负反馈调节电压的稳定性,同时实验中可采用集成控制芯片以增大电路稳定运行下的输入电压范围。
2.4 仿真分析
反馈补偿网络是稳压调理电路的核心,本文采用超前-滞后补偿网络。图5所示的闭环系统框图是图3稳压调理电路的简化表示。其中,Gc(s)为补偿网络的传递函数,Gm(s)为 PWM 器的传递函数,H(s)表示反馈分压网络的传递函数,可用α表示。
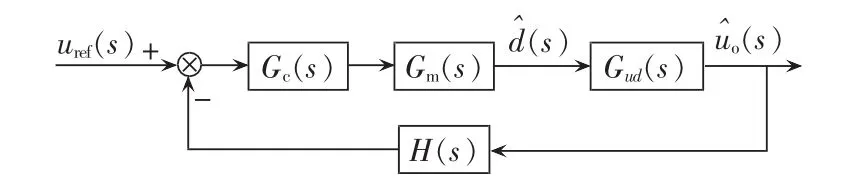
图5 调理电路闭环系统框图Fig.5 Block diagram of close-loop system of conditioning circuit
图5所示闭环系统的原始回路增益函数Go(s)可表示为式(24),其中,Um表示PWM器的锯齿波幅值。
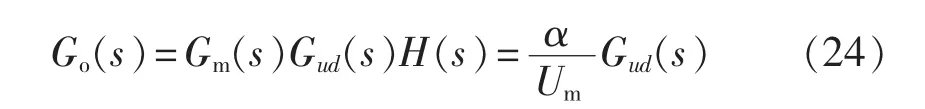
设PWM器的锯齿波幅值Um为2.5 V,反馈分压网络的传递函数α为1,将调理主电路参数代入式(24)便得调理电路的原始回路增益。结合传递函数幅频特性的波特图,设计得到调理电路补偿网络的传递函数 Gc(s):
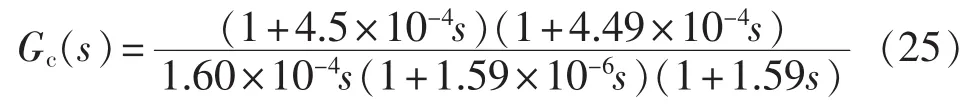
根据主电路参数以及求得的补偿网络的传递函数 Gc(s),并按照图3搭建仿真电路。 设电路在 0.5~0.52 s期间,输出电阻由 1 kΩ 突变为 100 Ω,模拟无线传感器作为负载时,由休眠转至信号发射的状态。调理电路输出电压仿真结果如图6所示。
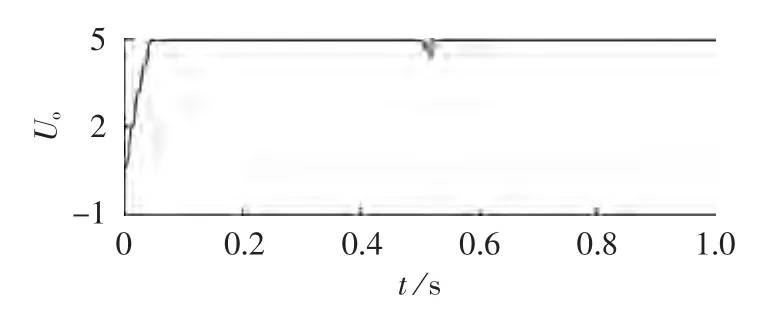
图6 调理电路输出电压的仿真结果Fig.6 Simulative results of output voltage of conditioning circuit
在 0.5~0.52 s期间,负载迅速减小,输出功率瞬间增大,从图6中可以看出,调理单元输出电压在负载突然增加时,会有短时间跌落,随后又很快恢复到原来的电压水平。仿真结果表明,该调理单元具有良好的稳压特性。
3 实验研究
为对包含调理电路以及电容集能拓扑的完整的自供能系统进行研究,搭建自供能实验平台。由于在外电场强度变化较大时,球冠型集能拓扑的输出电压特性优于平板型,因此实验中主要研究球冠型集能拓扑与调理电路配合的工作性能。
实验中稳压调理电路的开关选择型号为IRF540的N型场效应管。它具有极低的导通电阻36 mΩ,导通电压为1.7V,上升沿时间和下降沿时间分别为97ns和52ns,当开关频率低于1kHz时,功率低于100mW,适合低功耗应用。控制芯片采用TI公司生产的低功耗集成电压型PWM控制器TL5001CP,其工作的输入电压较宽,在3.6~40 V之间。待机工作电流为1 mA,正常供电电流约为1.4 mA,总体功耗较低,适合于低功耗场合应用。由于开关的控制端与输入端不共地,因此还需光耦对驱动信号进行隔离。选用TLP250低功耗光耦芯片,内部集成有GaAlAs发光二极管和光敏检测器,功耗约为100 mW。
本实验中稳压调理电路输入端采用的是高20cm、半径15 cm的球冠型集能拓扑,输出端为一个超级电容器,该电容的额定电压为2.7 V,大小为5 F,其主要作用是收集集能拓扑收集到的电能。实验时,首先需要将稳压电路中的储能电容充电至2.5 V,为稳压电路提供初始能量,以确保稳压电路中的开关及其控制电路在初始状态下动作。实验中,若输出端的电容无法获得转换器收集到的能量,则电路中开关及其控制电路在耗尽电容中的初始能量之后将停止动作。当稳压电路输出端的电容充电至2.5 V时,其储能为15.6 J。开关及其控制电路功耗以300 mW计算,则开关及其控制电路耗尽初始能量约耗时1 min。如果在施加工频电场之后,稳压电路中电容两极板电压可以维持在一个较为稳定的数值,则说明该自供能系统的“自持性”可以满足。
依上所述,将稳压电路中的超级电容充电至2.5V后,施加工频电场,电场强度为10 kV/m,5 min后测量电容两极板间电压波形,如图7(a)所示。
由图7(a)可知,稳压电路中的电容在初始充电至2.5 V后,两极板间电压稳定在2.6 V左右,高于初始值,因此该自供能装置可以实现电场能的收集。图7(b)所示为外施工频电场强度由5 kV/m逐渐增加至10 kV/m时稳压电路中储能电容的电压波形,从图中可以看出,调理单元输出电压稳定且具有良好的稳压效果;图7(c)所示为外施工频电场强度由10 kV/m逐渐减小至5 kV/m时,储能电容的电压输出波形,电容电压随外电场场强的降低而减小,但最终稳定在2.6 V。

图7 储能电容电压和外电场强度波形Fig.7 Waveforms of storage capacitor voltage and external electric field intensity
但当外电场强度继续降低,由5 kV/m降低至3 kV/m时,储能电容的电压将无法维持在2.6 V,而是随外电场强度的降低而减小,如图7(d)所示。这是由于随着外施工频电场强度的降低,自供能装置收集到的能量也随之减少,由于调理单元的正常运行需要一定的能量,当自供能装置收集到的能量小于调理单元运行所需的能量时,储能电容将无法得到充足的电能,因此电容的电压降随着外电场强度的降低而下降。
4 结论
本文主要对空间电能集能转换器进行了理论和实验研究。针对平板型集能拓扑的集能缺点提出球型集能拓扑,并对其进行数学建模,确定了球型拓扑集能效果的影响因素。考虑实际变电站应用,对球型拓扑进行结构上的改进,提出球冠型拓扑结构。对稳压调理电路进行系统建模,包括大信号和动态小信号模型,并借此分析调理电路的工作特性和补偿网络的参数选择。考虑到外电场不断变化,仿真分析了调理主电路在外电场变化下的运行特性。最后,搭建了电容式集能转换器实验平台,在实验模拟的工频均匀电场下验证自供能系统的整体运行性能。
空间电能集能转换器如要投入实际应用面临的最主要问题是解决集能转换器容性内阻抗过大的问题,解决方法主要有2种:一种方法是增大转换器两极板间的介电常数ε,比如采用油纸绝缘等;另一种方法是增加集能转换器的表面积。但这2种方法也会相应带来高压变电站内现场安装的困难与安全隐患。

