基于无源性控制的变压器低频加热电源
朱小帆,查晓明,秦 亮,黄 坡
(武汉大学 电气工程学院,湖北 武汉 430072)
0 引言
变压器作为电力系统运行的核心器件之一,其良好的绝缘性能是电力系统安全运行的重要保障。当变压器长期暴露在空气中时,变压器油容易受潮,而变压器的绝缘材料具有一定的亲水性,易导致变压器绝缘性能下降,时刻威胁着变压器的安全运行。因此,变压器的干燥十分必要。传统的加热干燥方法,如涡流加热法、热风干燥法、真空干燥法,存在操作复杂、暴露在空气中绝缘易氧化、加热效果不均匀、加热干燥时间较长等缺点[1]。为此设计了一种基于无源性控制的低频加热电源LFHS(Low-Frequency Heating Source)。LFHS通过输出低频电流来降低负载变压器中感抗的影响,可以在电压远低于负载变压器额定电压的情况下使电流达到负载变压器的额定电流,保证良好的加热效果。由于直接利用负载变压器的线圈绕组加热,LFHS避免了加热不均匀、暴露在空气中绝缘易氧化的缺点,且操作简单。LFHS利用交-直-交变换原理,为了提高电压等级,整流侧由1个隔离变压器和2个级联的不控整流桥构成,逆变侧主拓扑采用中性点箝位NPC(Neutral Point Clamped)三电平结构,此结构具有输出功率大、开关损耗小、谐波含量少的特点。
NPC三电平结构的弱点在于其直流电容电压容易产生不均衡,可以从改变硬件拓扑和优化控制算法2种途径保证直流电容电压均衡,改变硬件拓扑会使结构变得复杂、成本增加,相对而言优化控制算法更容易实现;在参考电压上叠加适当的零序电压分量可以达到保持直流电容电压均衡[2-9]的目的。文献[4]从机理上研究了注入零序分量的类型,文献[9]中优化了注入零序分量的计算方法,提出了一种简单实用的零序分量预估-校验-修正算法。本文通过中点电流计算公式,求得所需零序分量直接代入无源性控制模型,同时求解所需参考电压的正序分量和零序分量,更易于工程实现。
无源性控制理论是研究非线性系统稳定性的重要工具,它是一种能量整形的方法,通过配置系统的能量和注入非线性阻尼,迫使系统总能量跟踪期望的能量函数,并使系统的状态变量渐近收敛至设定值,达到要求的性能[10-13]。它的物理意义在于表明系统的能量由初始时刻到目前时刻的增长量总是小于等于外部注入的能量总和。这是一种全局定义且全局稳定的控制方法,无奇异点,控制器的设计简单,鲁棒性强[14-18]。本文基于无源性控制理论,设计无源性控制比率,确保了对指令电流的渐近跟踪;通过给定指令电流,实现了LFHS对低频电流的控制。仿真结果表明,此控制算法能够在输出低频电流的同时实现直流电压的均衡控制,且稳态特性好、动态响应速度快、算法实现简单、鲁棒性强。380 V、700 kV·A的工程实际应用表明该LFHS起到很好的加热作用。
1 LFHS的电路分析
1.1 主电路拓扑
LFHS的主电路拓扑如图1所示,其输入侧接入市电380 V,输入电源分为2路,一路直接接入不控整流桥,另一路通过隔离变压器和不控整流桥,旨在建立较高的直流电压udc,经过变换后接入负载变压器,二极管箝位三电平逆变器中的开关器件IGBT的导通与关断均通过正弦脉宽调制SPWM(Sine Pulse Width Modulation)控制。LFHS的主要任务是在保证直流电压均衡的前提下,输出用于负载变压器加热的低频电流。

图1 LFHS主电路拓扑Fig.1 Main circuit topology of LFHS
为了便于分析,假设udc为一恒定的直流电压;C1、C2为直流分压电容,C1=C2=C;udc1、udc2分别为 C1、C2上的直流电压;ia、ib、ic分别为 a、b、c 三相的输出电流;ula、ulb、ulc为接入负载变压器的三相电压;o 为电压中位点;io为中线总电流;VT1、VT2、VT3、VT4为 a 相桥臂上的4个IGBT;VD1、VD2为a相桥臂的箝位二极管;Ra、Rb、Rc分别为 a、b、c 相的等效串联损耗电阻;Lla、Llb、Llc分别为 a、b、c 相联接电抗器。
1.2 数学模型
令 NPC 逆变器的开关函数为 Sx(x=a,b,c),以 a相为例:

同理可得Sb、Sc,根据图1所示拓扑结构,基于基尔霍夫电压定律可以得到如式(2)所示方程:

由于开关函数Sx为断续函数,无法进行无源性控制,为了方便分析,根据PWM的控制原理,在一个控制周期内开关状态输出的平均效果与参考电压等效,由此可得式(2)所示的状态平均模型:
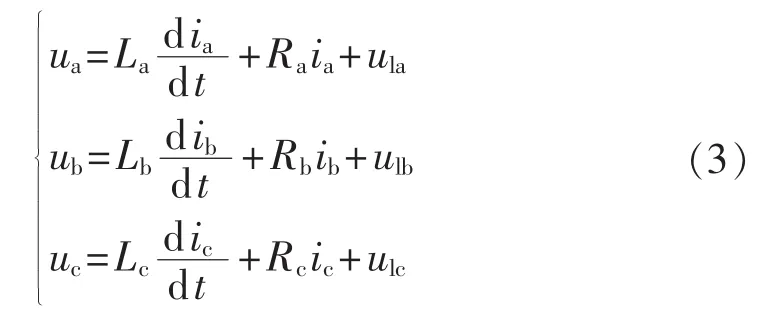
其中,ua、ub、uc为逆变器控制的三相参考电压。
2 LFHS的无源性控制
2.1 直流电容电压均衡控制
对于NPC三电平逆变器的拓扑,由于器件参数不同等原因,在能量交换的暂态过程中直流侧电容电压不能保持均衡,即中点电位发生偏移。中点电位偏移会导致NPC三电平逆变器的输出产生谐波,影响负载性能,失衡严重时甚至会导致逆变器本身器件损坏,造成事故。直流电压均衡即为:

由基尔霍夫电流定律可知:

如果直流电容电压存在偏差,对方程(5)在一个控制周期Tc内积分,可以求得中点电流的控制量为:

令三相正序参考电压为:

其中,M为调制比。在三相正序参考电压上叠加零序电压分量u0,可以得到实际的参考电压为:

控制NPC三电平逆变器的直流电压均衡等效为控制中线电流io=0,而只有当NPC三电平逆变器的开关状态处于中点箝位状态即Sx=0时,才会有中线电流io≠0,故中线电流可以表达为:
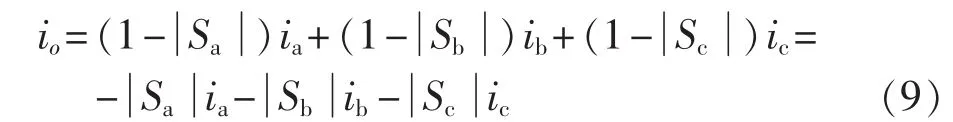
根据PWM的控制原理,在一个控制周期内开关状态输出的平均效果与参考电压等效,令符号函数为:

根据式(9)和式(10)可以得到一个控制周期内的平均中线电流iop为:
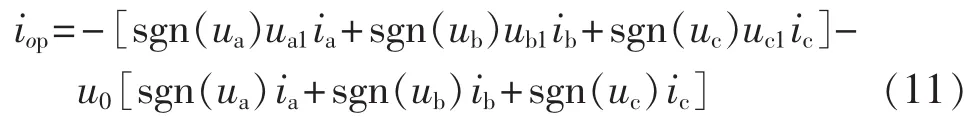
若保持直流电压均衡则必须满足iop=0,由此可以求得需要叠加的零序电压u0:
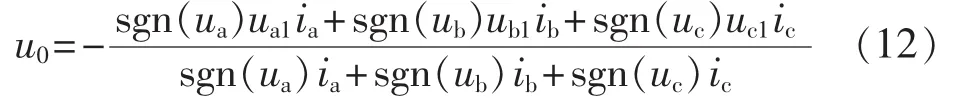
约束条件为:

其中,umax=max(ua,ub,uc);umin=min(ua,ub,uc)。
2.2 无源性控制

其中,A=diag[LaLbLc]为一正定对角阵;对称正定矩阵 R=diag[RaRbRc],反映了系统的耗散特性;F=[ua-ula,ub-ulb,uc-ulc]T为系统与外部交换的能量。
设置反馈阻尼为:
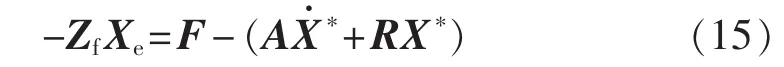
其中,Zf=diag[zfi](i=1,2,3)为阻尼系数矩阵,且zfi>0。 式(15)代入式(14)可得:

对于误差方程(14),选择能量存储函数为:

对方程(17)等号两边求导,并联立式(16)可得:
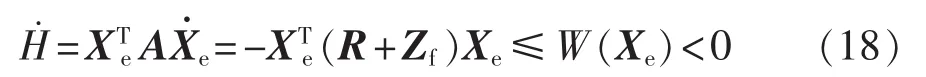
其中,W(Xe)=-β‖Xe‖2,β>0,‖Xe‖为Xe的Euclidean范数。由上式可知,误差方程在Xe=[0 0 0]T处渐近稳定,确保对控制目标X*的渐近跟踪。
将式(8)代入式(15),并联立式(12)可得:

由于负载变压器为三相对称固定参数负载,所以可以通过上式求解得到逆变侧控制的正序参考电压ua1、ub1、uc1和所需要注入的零序电压u0。由此可得LFHS逆变侧的无源性控制框图如图2所示。
由上述推导可知由式(14)表示的误差系统为欠驱动系统,在理想情况下,可以在保证直流电压均衡即Δu*dc12=0的同时实现对任意的渐近跟踪。

图2 LFHS无源性控制框图Fig.2 Block diagram of passivity control for LFHS
3 仿真与工程试验
3.1 仿真研究
为了验证此控制算法的有效性,基于PSCAD/EMTDC软件仿真平台,根据实际装置元件参数构建了输入电压为380 V、装置容量为750 kV·A的LFHS无源性控制仿真模型。LFHS不控整流桥1联接的隔离变压器变比为 1∶1.28,容量为 0.5 MV·A,直流母线的2个串联电容均为20000 μF,由于负载为变压器,装置输出的联接电抗器为1 μH,等效损耗串联电阻为0.001 Ω。负载变压器高压侧电压等级为110 kV,容量为 30 MV·A,正序漏抗为 0.1 p.u.,空心电抗为 0.2 p.u.。
根据设计要求,在不超过装置自身容量和负载限制的情况下,LFHS装置指令低频电流的大小可以随时变化;输出电流指定频率的范围设置为0.2~1 Hz,设置频率上限是为了防止由于输出电流受到负载变压器感抗影响过大而无法达到指令电流值,设置频率下限的目的是防止负载变压器磁饱和。所以将仿真流程设置为:0~0.3 s为装置启动过程;0.3~2 s LFHS的指令电流大小(指令电流均指电流有效值)为50 A、频率为1 Hz;2~4 s增加LFHS的指令电流至80 A,降低频率至 0.5 Hz;4~6 s提高 LFHS的指令电流至95 A,降低频率至 0.2 Hz。
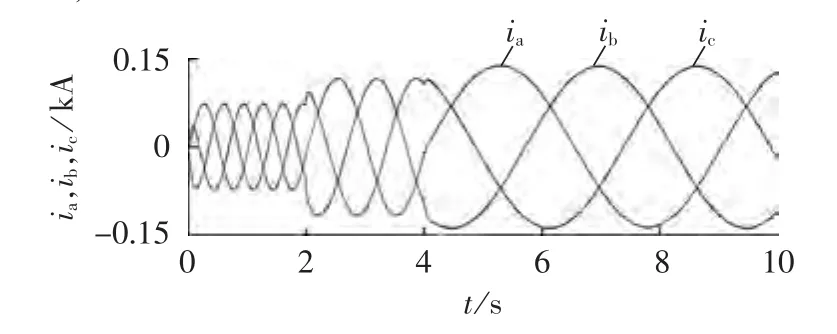
图3 无源性控制下三相电流Fig.3 Three-phase current under passivity control
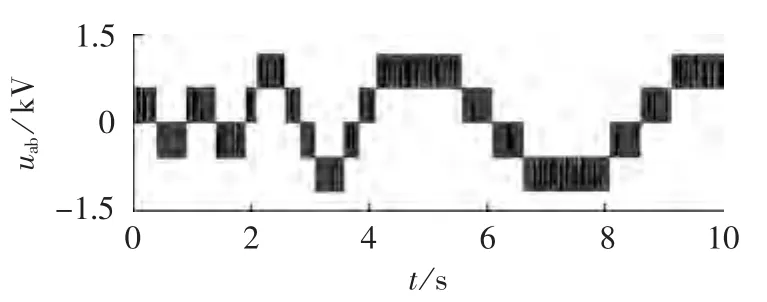
图4 无源性控制下线电压uabFig.4 Line voltage uabunder passivity control
图3所示为无源性控制下LFHS三相输出电流的波形,图4所示为无源性控制下LFHS输出的a相与b相间线电压uab。由图3和图4可知,在无源性控制下,改变LFHS指令电流的频率和大小,LFHS都能够快速响应,准确跟踪指令电流。
图5为无源性控制下2个直流电容电压udc1和udc2的波形。 在 0.3~2 s内,udc1和 udc2波动范围为600~601 V,直流电容电压均衡控制效果良好;在2~4 s内,图5中圆圈处可以看出直流电容电压udc1和udc2波动范围下降至 595~596 V;在 4~10 s内,udc1和udc2波动范围为594~597 V。原因为仿真中的直流电源为非理想电源,由0.5 MV·A的隔离变压器和2个不控整流桥构成,但是直流电容电压的均衡控制效果仍然良好,直流电容电压偏差低于0.5%。
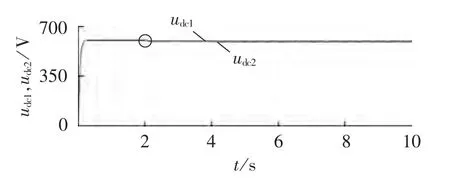
图5 无源性控制下udc1和udc2Fig.5 udc1and udc2under passivity control
由仿真结果可以看出,在LFHS指令电流的大小和频率发生变化时,LFHS通过无源性控制能够快速准确地跟踪指令电流的变化,而且可以很好地维持直流电压均衡,保证输出电流的大小和频率满足指令要求。
3.2 工程试验
基于无源性控制的LFHS装置在110 kV主变成功试验。装置参数为:输入电压为380 V,装置容量为750 kV·A;装置的电源由1.5 MW的备用电源车提供;隔离变压器变比为 1∶1.28,容量为 500 kV·A;上下2组直流电容均为采用10000 μF/400 V的直流电解电容四串八并,等效容值为C=20000 μF;由于负载为变压器,所以没有额外再加联接电抗器,负载变压器为型号SF10-31500/110的110 kV主变,将负载变压器的低压侧短路,LFHS输出接入负载变压器的高压侧。IGBT的型号为FZ800R12KE3。
控制器的实现由可编程逻辑控制器PLC(Programmable Logic Controller)、数字信号处理器 DSP(Digital Signal Processor)、现场可编程门阵列 FPGA(Field Programmable Gate Array)和复杂可编程逻辑器件CPLD(Complex Programmable Logic Device)4个部分组成。PLC可靠性高,抗干扰能力强,用于开关量逻辑控制以及人机界面数据交换。DSP指令执行速度快,具有快速中断响应与处理能力,用于有效值计算以及装置系统级的保护,包括交流过压、交流欠压、输出过流、输出速断和TV断线保护等。FPGA具有体系结构和逻辑单元灵活、集成度高以及适用范围宽等特点,用于基于无源性控制理论的无功电流控制和直流电压稳定控制,以及利用功率单元相互作用的直流电压均衡控制。CPLD放在功率单元驱动板上,在产生精确的死区时间的同时,实现功率单元直流电压的采样和保护(直流电容电压偏差保护参考值为30 V)、IGBT温度的采样和过热保护等。
LFHS的实际装置由隔离变压器、开关柜、功率柜和控制柜组成。硬件控制器框图如图6所示,其中人机界面与DSP采用RS-485通信,DSP与FPGA通过DSP的公共数据线、公共地址线、读写使能线、地址片选线及FPGA的IO口交换数据,FPGA与CPLD通过2根光纤实现命令下发和数据交换,并通过3根光纤发送PWM信号,CPLD生成的开关控制信号通过M57962控制功率单元中IGBT的通断。

图6 LFHS硬件控制器框图Fig.6 Block diagram of hardware controller of LFHS
图7所示为LFHS指令电流大小为60 A、电流频率为0.5 Hz时,a相输出电流波形及2个直流电容电压波形。图8所示为LFHS指令电流大小为110A、电流频率为0.2 Hz时,a相输出电流波形及2个直流电容电压波形。图9所示为LFHS指令电流大小为110 A、电流频率为0.2 Hz时,ab相线电压波形。
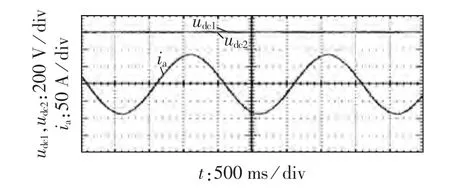
图7 输出电流和直流电容电压波形(f=0.5 Hz)Fig.7 Waveforms of output current and DC capacitor voltage(f=0.5 Hz)

图8 输出电流和直流电容电压波形(f=0.2 Hz)Fig.8 Waveforms of output current and DC capacitor voltage(f=0.2 Hz)

图9 ab 相线电压波形(f=0.2 Hz)Fig.9 Waveform of uab(f=0.2 Hz)
由图7—9可以看出,LFHS的工作频率为0.5 Hz和0.2 Hz时,在无源性控制下,输出电流可以很好地跟踪指令电流,电流波形输出基本正弦;由于LFHS是一个容量为5 MW的备用电源车,在LFHS的指令电流增大时,直流电容电压产生了一个较小的下降。由LFHS的人机界面记录了指令电流分别为60 A和110 A时直流电容电压的10组数据如表1所示。
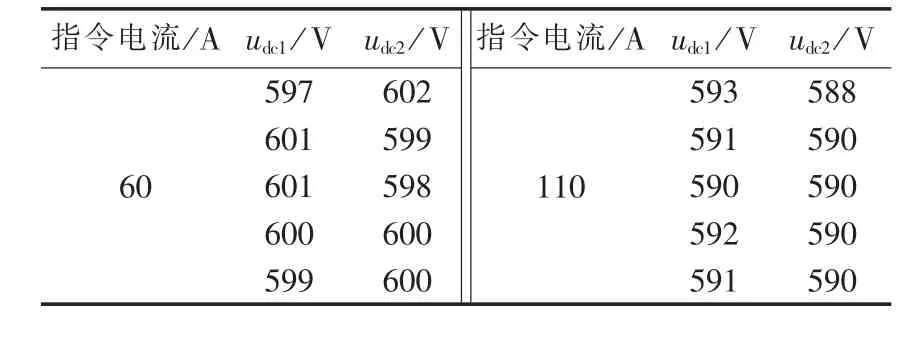
表1 人机界面显示直流电容电压Table1 DC capacitor voltages displayed on man-machine interface
由表1可以看出,当指令电流为60 A时直流电容电压的波动范围为597~602 V,最大偏差电压为5 V;当指令电流为110 A时直流电容电压的波动范围为588~593 V,最大偏差电压仍为5 V,由此可以说明总的直流电压虽然有所下降,但是直流电容电压仍然保持良好的均衡效果。在没有投入直流电容电压均衡控制环节的情况下,LFHS的直流电容电压偏差会随着输出电流增大而变大,当输出电流为27 A时,触发了直流电容压差保护30 V,从而导致装置封锁IGBT控制脉冲。
由于负载变压器已经脱离电网,而且没有温度采样接口,无法精确监测绕组温度和油温,故采用红外成像仪监测负载变压器的油温,并每隔1 h记录负载变压器的最高局部油温。在低频加热电源输出电流大小为110 A时温度记录如表2所示。
LFHS 现场工作试验时间为 10∶00—21∶00,环境温度最高11°C,最低3°C。由表2的数据可以看出:在加热开始阶段,温度上升较慢;加热1 h后,温升速度大概保持7°C/h;9 h后油温基本稳定保持在67°C左右。导致温升速度7°C/h与最终稳定温度为67°C的主要原因为环境温度较低,夜间环境温度下降至3°C,如果能辅以保温措施,将能够取得更好的加热效果。由此可以看出无源性控制算法可以使LFHS在保证直流电容电压均衡的条件下输出完好的低频加热电流,为负载变压器加热。
4 结论
本文针对目前变压器加热干燥存在的受热不均、绝缘受损等问题设计了一种新型的LFHS,并提出了应用于LFHS的无源性控制方法。通过理论推导、仿真实验证明了该控制算法的可行性,并经过实际工程应用验证基于无源性控制的LFHS能够达到在保证直流电容电压保持均衡的条件下,快速跟踪指令低频电流,为变压器加热方法提供了新的思路和参考。

