中考题中也有“皮克公式”的身影

袁少卿

回到家，我就激动的把今天上课的收获告诉了当数学教师的爸爸.爸爸笑着说：“掌握公式还不够，要掌握获得知识的过程和方法，让我来考考你.”他找到了2013年常州市的中考卷的倒数第三题，我惊讶道：“皮克公式在这也会有用武之地？”

（2013·常州）用水平线和竖起线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S，该多边形各边上的格点个数和为 ，内部的格点个数为b，则S= +b﹣1（史称“皮克公式”）.

小明认真研究了“皮克公式”，并受此启发对正三角形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：

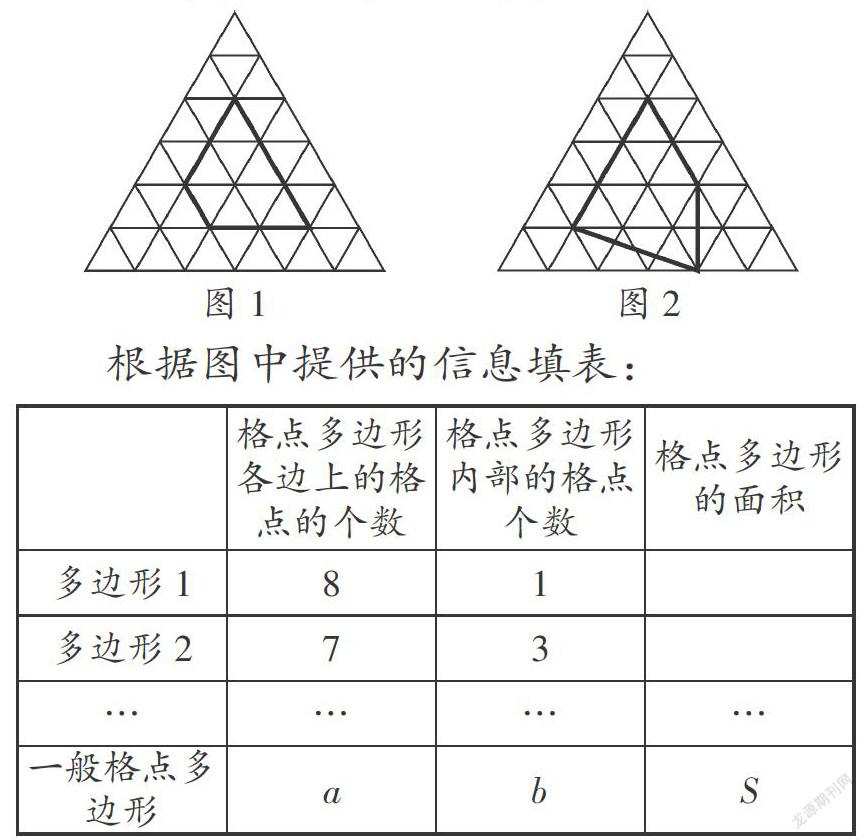
读完题，我非常有信心能把这题解出来.与原来背景唯一不同的就是将正方形网格换成了正三角形网格.很轻松的，第一行应该填8，第二行应该填11.我笑眯眯地朝着老爸说：“老爸，这题也太简单了，下面只要我去寻找规律就行了，真的没什么技术含量.”老爸笑而不语.我又开始埋头苦干起来，果然局势突变，我试图多次，很难以从仅有的两组数据达成统一的共识.我不想动脑筋的老毛病又犯了，开始找借口为自己脱身，翘着嘴向老爸求情：“爹地，看在我才是初一学生的份上，这题等我长大些再做吧.”老爸双手一摊，说道：“你再想想今天你是通过怎样的过程知晓皮克公式的？”老师上课的一幕幕又在眼前浮现，“哦哦哦哦，我应该创作更多的图，获取更多的数据.内部格点个数为0的情形，一个小正三角形不就是吗？此时 =3， b=0， S=1，两个小正三角形拼成的平行四边形也对啊！此时 =4， b=0， S=2，三个拼成的梯形情形： =5， b=0， S=3，四个拼成的正三角形还符合啊！我再记下来，这样的数据多多益善啊！此时 =6， b=0， S=4.这也太明显了，S= -2嘛！欣喜之情很快褪去，当内部格点个数为1时，S≠ -2，此时S= ，让我再画几个情形看看，果然依然符合.下面我又画了几种特殊情形，发现当内部格点个数为2时，S= +2，当内部格点个数为3时，S= +4，规律逐渐明朗， 后面加的数都是偶数，而且都是2×（内部格点数—1），所以结论是S= +2（b-1）.老爸打开答案，我手舞足蹈，“对喽对喽”声此起彼伏.

嘿嘿，同学们，我会做中考大题了，相信你也一定行的！

（指导老师：王正海）