认识线和角

生活中许多美妙的图形，是由线和角构成的.在《平面图形的认识（一）》这一章中通过丰富的实例，认识了线段、射线、直线、角等简单的平面图形，了解平面上两条直线的平行与垂直关系，这些都是进一步研究其他图形性质的基础.

一、线段、射线、直线

1、线段、射线、直线的区别与联系

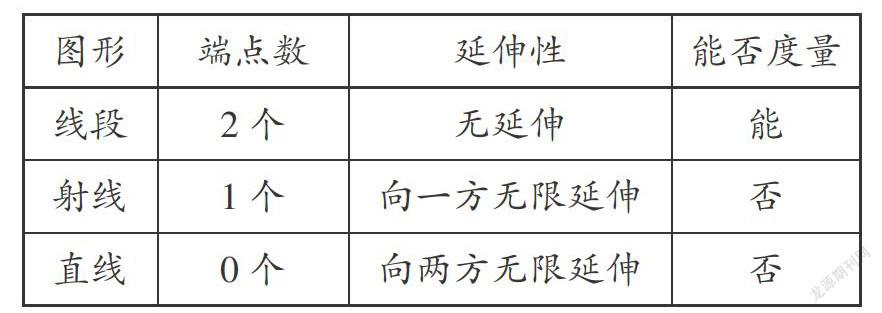
线段、射线、直线的区别在于有无延伸性和有无端点，线段向一方无限延长形成射线，向两方无限延长形成直线.在用符号表示线段、射线、直线时，一般应在字母前面注明“线段”、“射线”、“直线”.

2、线段的大小比较

（1）叠合法：先把两条线段的一个端点重合，使另一个端点在同一侧，从而确定两条线段的长短，这是从“形”的方面进行比较.

（2）度量法：先分别量出每条线段的长度，再根据度量的结果确定两条线段的大小，这是从“数”的方面进行比较.

3、线段的中点

把一条线段分成相等的两条线段的点叫做线段的中点.

如图，因为C是线段AB的中点，所以AC=BC= AB或AB=2AC=2BC.

二、角

1、角的定义和表示方法

角可以从静态和动态两种方式给出定义.

（1）角的静态定义：角是由有公共端点的两条射线组成的图形；

（2）角的动态定义：角也可以看成是一条射线绕着它的端点旋转到另一个位置所成的图形.起始位置为始边，终止位置为终边.

在对角进行表示的时候，应注意：

（1）用三个大写字母表示角时，顶点字母一定要写在中间的位置；

（2）用一个大写字母表示角时，这个顶点处只能有一个角；

（3）用数字或希腊字母表示角时，要在角内靠近顶点处画上弧线，并注上数字或希腊字母.

2、角的大小比较

与线段的大小比较类似，比较两个角的大小有叠合法和度量法.

（1）叠合法：将两个角的顶点和一边叠合在一起，另一边放在重合边的同侧，观察这两条边的位置关系；

（2）度量法：用量角器量出要比较的角的度数直接比较大小.角的度量单位是度、分、秒，相互之间的换算是六十进制，类似于时、分、秒的换算.

角的大小决定于角的两条边张开的角度，与边的长短并没有关系，例如，用一个放大5倍的放大镜看一个30°的角，这个角在放大镜下仍然是30°.

3、角的平分线

从角的顶点引一条射线，把这个角分成两个相等的角，这条射线就是这个角的角平分线.

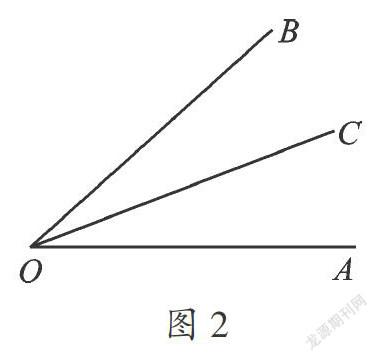
角平分线的性质与线段的中点的性质类似，如图，因为OC平分∠AOB，所以∠AOC=∠BOC= ∠AOB，∠AOB=2∠AOC=2∠BOC.

三、两个角之间的特殊关系

1、 余角、补角

（1）定义：如果两个角的和是一个直角，那么这两个角互为余角；如果两个角的和是一个平角，那么这两个角互为补角.

需要注意的是：互余、互补指的是两个角在数量上的特殊关系，与它们所处的位置无关.只有锐角才有余角，互余的两个角都是锐角，互补的两个角都小于180°.

（2）性质：同角（等角）的余角相等；同角（等角）的补角相等.

2、对顶角

（1）定义：如果两个角有公共顶点，而且一个角的两边分别是另一个角的两边的反向延长线，这样的两个角叫做对顶角.

对顶角的概念揭示的是两个角位置上的特殊关系，在相交的两条直线中，相对的两个角是对顶角.

（2）性质：对顶角相等.

根据对顶角特殊的位置关系，利用“同角的补角相等”可以推出“对顶角相等”的数量关系.

四、两条直线之间特殊的位置关系

1、平行

（1）平行线的概念

在同一平面内，不相交的两条直线叫做平行线.

同一平面内，两条直线的位置关系有两种：相交和平行（不相交）.注意：①在“同一平面内”是前提条件；②平行线指的是两条直线，如果两条射线或两条线段平行，实际上是指它们所在的直线平行.

（2）平行线的基本性质

过直线外一点有且只有一条直线与这条直线平行.

“有且只有”说明了平行线的存在性和唯一性，同时过直线上一点不能作直线与这条直线平行.

2、垂直

（1）垂线的概念

如果两条直线相交成直角，那么这两条直线互相垂直，互相垂直的两条直线的交点叫做垂足.当两条直线互相垂直时，其中一条直线叫做另一条直线的垂线.

在同一平面内，两条直线只有相交与平行两种位置关系，“垂直”是相交的一种特殊情形.

（2）垂线的性质

①过一点有且只有一条直线与已知直线垂直.

它同样说明了垂线的存在性与唯一性.与平行线的性质不同的是，这一点的位置可以在直线上也可以在直线外.

②垂线段最短.

直线外一点到这条直线的垂线段的长度，叫做点到直线的距离.

在学习中，应注意区分垂线、垂线段、点到直线的距离.垂线是直线，垂线段是线段，它们都是图形；点到直线的距离是用垂线段的长度来定义的，它是一个数量.