设计过渡性问题应把握“六性”
荀步章
许多教师常常会向学生提出许多琐碎的问题,学生只能一个一个琐碎地回答。如果教师能对问题进行有效整合,设计一个合适的“过渡性问题”,不仅可以使学生顺利进入问题研究,还可以使其思维既深刻又顺畅。因此,教师要精心设计“过渡性问题”,让儿童更快地通过智力发展的各个阶段,更深刻地理解数学本质。
一、 把握层次性
【片段】“射线的认识”教学片段
师:我们来玩一玩激光棒,对着窗外射,会射到哪里?
生:有可能射到外面房子上,也有可能射到山上。
师:假设外面什么物体也没有,会出现什么情形?
生:光线会无限长,没有止境。
师:请同学们闭上眼睛想一想,在你心目中这条无限长的光线是什么样的。
师:(想了一会儿后)谁能用自己的话说一说你刚才想象的“无限长”是什么样的?给同学们描述一下。
生:我想象无限长就到了地球的对面,到了外国。
师:同学们评价一下他说的算不算无限长呢?
生:不算,只能说是非常长,按他说在很远的地方还有物体,还有小红点。
生:我认为无限长是永远都不会停下来。
生:我认为无限长就是永无止境地延伸下去。
……
【分析】要让儿童建立“无限长”的表象,十分困难,只能借助想象,“无限长”看不见,摸不着,但能想象。通过常见的激光棒发光,分层探究“激光棒的光会射到哪里”“什么物体也没有会怎样”“无限长的光线是什么样的”,把学生引进想象的殿堂,展开想象的翅膀,点燃思维火花,经历对“无限长”的空间思考。数学教学的实质是学生与数学知识发生联系的过程,使静态的书本知识内化为动态的学生数学思维。通过“过渡性问题”,让学生真正去“想数学”“经历数学”,提升对问题的理解,真正建立起“无限长”的空间观念。
二、把握“旧知性”
【片段】“小数乘整数”教学片段
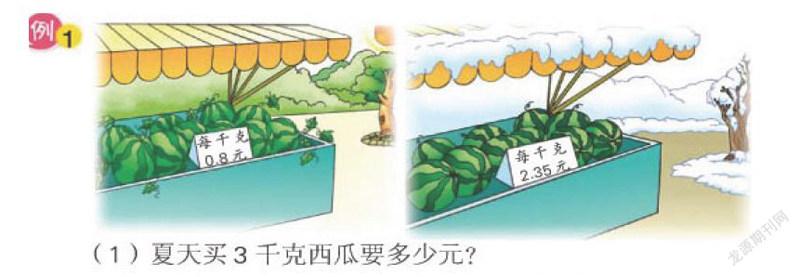
师出示挂图如下,引导学生展开讨论。
生:要求3千克西瓜多少元?用0.8×3,这个还没学过。
师:0.8×3到底等于多少?我们能联系已经学过的知识想一想、算一算吗?
生:0.8×3就是3个0.8相加,0.8+0.8+0.8=2.4(元)。
生:0.8元=8角,8×3=24(角),24角=2.4元。
师:同学们真了不起,想出了这么好的办法来解决这个新问题。你们在不知不觉中把新问题转化成了旧知识。
师:把新知转化成旧知,这种方法就叫转化,在今后学习数学时经常会用到这种方法。如果要求冬天买3千克西瓜要花多少钱,怎么列式?
生:2.35×3。
师:同学们也大胆地算一算,等于多少呢?
……

【分析】要解决“0.8×3”,教师创设了一个买西瓜的情境,让学生“联系已经学过的知识想一想、算一算”,借助旧知解决问题,让学生对转化的数学思想有了初步的了解,“转化”在今后解决新问题的过程中经常使用。设计买东西的情境,把数学问题与生活实际产生联系,旧知能够帮助儿童解决新问题,积累了基本的生活经验。因此,设计“过渡性问题”要充分关注学生已有的生活经验,更要提升他们的生活经验,经验只是载体,需要在实践中体验,经历数学思考过程。
三、把握图像性
【片段】“真分数、假分数的认识”教学片段
课堂练习时,师出示图1。
师:图1中阴影部分用什么分数表示?
生:用表示,把单位“1”平均分成4份,表示其中的5份。
生:不对,应该用表示。
生:阴影部分一共涂了5份呀!
生:单位“1”是两个圆,下面有一个大括弧。
师:究竟是,还是?再看一看图2,比较图1和图2有何区别?
生:图1有一个大括弧,图2没有。
生:图1中的大括弧表示把两个圆合起来看作单位“1”。
生:图2只是把一个圆看作单位“1”。
生:图1阴影部分表示成,图2阴影部分表示成。
【分析】学生误认为把每个圆看作单位“1”,这就构成了认知难点。为突破这一难点,借助直观图像,引导观察图1和图2,发现差异,让学生自然调整思考方向。把“过渡性问题”图像化,使学生思维走向纵深,更加清晰理解分数的本质,把单位“1”平均分成若干份,“表示这样的”而不是“取其中的”一份或几份,又一次强化了真分数和假分数之间的内在联系。在活动过程中丰富了儿童的感性认知,克服了前概念对后继学习的影响。
四、把握差异性
【片段】“解决问题的策略——列举”教学片段
师出示教材中一道习题:一张靶纸共三圈,投中内圈得10环,投中中圈得8环,投中外圈得6环。小华投中两次,可能得到多少环?
师:这个问题的关键之处是什么?
生:投中。
师:投中两次有哪些可能?
生:两次环数相同和两次环数不同。
师:你们能把所有可能的情况不重复、不遗漏地列举出来吗?
生:两次环数相同的有:10+10=20(环),8+8=16(环),6+6=12(环);投中两次环数不同的有:10+8=18(环),10+6=16(环),8+6=14(环)。
生:6种可能性,得到20、18、16、14、12环五种不同结果。
师:如果改一个字,小华投了两次,可能得到多少环?
师:这个问题的关键之处是什么?
生:投了。
师:投了两次有哪些可能?
生:投中两次,投中一次,两次都没中。
生:投中两次又分两次环数相同和两次环数不同。
生:投中两次与刚才一样;投中一次分别得到10、8、6环三种情况;两次都不中得0环;一共有20、18、16、14、12、10、8、6、0环九种不同结果。
【分析】从“投中两次”到“投了两次”一字之差,问题的复杂性随之增加,对儿童的挑战难度也在加大,策略运用的价值逐步体现。教材中的问题表述、语言提示方式、探究思路等方面,让儿童发现差异,比较差异,实现同化与顺应。从儿童的真实理解出发,有效介入“过渡性问题”,把问题解决的重点、儿童认知的难点化解,这是每一位教师的教学追求。
五、把握探索性
【片段】“圆的周长”教学片段
师出示正方形和圆形。
师:给你一把直尺,来测量这两个图的周长,你愿意测量哪一个?为什么?
生:我愿意测量正方形。因为正方形的边是直的,好测量,圆的边线是弯的,不太好量。
师:如果老师想为难你们,就用直尺量出圆的周长,敢挑战吗?(师出示一个荧光圈)
师:这个荧光圈的周长怎样测量?
生:可以把接头拔下来,拉直了,然后量一量。(师实物演示过程)
师:真不错,已经想到把弯曲的荧光圈转化成直直的线段了。
师(出示一个飞镖盘):这个飞镖盘,不能拉直,怎么办?
生:可以用线绕一圈,然后量出线的长度,就是飞镖盘的周长。
生:把飞镖盘在直尺上滚一圈,看一看滚多远,就是它的周长。
师:这些办法有一个共同特点,就是“化曲为直”。
师(出示一幅摩天轮图片):测量这个摩天轮,用刚才剪、滚、绕的方法适合吗?怎么办?
师(再次出示正方形和圆形):正方形的周长与边长有关,圆的周长可能与什么有关?
生:圆的直径。
生:圆的半径。
师(课件演示,引导观察):三个直径不同的车轮,同时向前滚动一周,你发现了什么?
生:直径越大,圆的周长就越大,直径越小,圆的周长就越小。
生:半径越大,圆的周长就越大,半径越小,圆的周长就越小。
师:我们都知道,正方形的周长是边长的4倍,猜想一下,圆的周长是直径的多少倍?
……
【分析】教师把圆形和正方形对比起来探究,在图形感知上,正方形的边线是直直的,每一条边都很容易测量,而圆形边线是弯弯的,不容易测量。在测量方式上,正方形周长可以根据一条边的长度进行计算,圆形不容易直接测量,需要想办法“化曲为直”,在探索圆与正方形周长的本质时,必须让学生经历“化曲为直”的思考过程。在关系研究上,先让学生猜想,再逐步去掉不合理的答案,范围由大到小,研究由粗到细,慢慢触摸“本质”。让学生发现规律,提出猜想,感受多样化的解决策略,在合作与交流中创生,寻求突破。
六、把握操作性
【片段】“认识体积”教学片段
教师请一位学生用眼罩把眼睛蒙起来,双手侧平举。教师在这位学生的左手挂一件大块塑料泡沫,右手挂一件小铁块。
师:请同学们不要提醒,让蒙眼的同学猜一猜,哪只手所挂物体体积大一些?
生:右手这边体积大一些。(摘掉眼罩,这位学生很惊讶)
师:你们有什么发现?
生:左手挂的物体体积很大,但重量很轻。
生:右手挂的物体体积很小,但重量比左手的重。
生:物体体积大的重量不一定重。
生:重量重的物体体积也可能很小。
师:体积是一个物体所占空间的大小,与它的重量不能混淆。那么,体积大的物体,它的表面积是不是就大呢?
师: 我们再来做一个实验,观察这两块橡皮泥,你有什么发现?
生:这两块橡皮泥一样大。
师:你指的是什么一样大?
生:体积。
师:现在老师把这块橡皮泥压扁,做成一块薄饼,你们有什么发现?
生:它的面积变大了。
师:你为什么不说它的体积变大了?
生:橡皮泥虽然形状变化了,表面积也变大了,但它的体积没有发生改变。
师:是呀!物体的表面积大,不表示它的体积也一定大,比如这两块橡皮泥,这块压扁的表面积很大,但它的体积和这块橡皮泥的体积是一样大的。
【分析】体积是比较抽象的概念,学生可能会和已有经验中的重量或面积发生混淆。教师通过两个操作示范,让儿童进一步体会体积的本质,通过掂重量对不同物体比体积,观察不同形状比体积,使儿童对体积的认识不断加深,体会到物体的体积不能简单片面地看重量与形状。“过渡性问题”的创设不仅仅是告诉儿童数学知识,更需要儿童亲身经历,在操作过程中感悟数学的魅力,积累基本的认知经验,发展儿童的数学素养。
学习通常是由一系列的片段组成的,一个学习片段,将其作用发挥到最佳,才能反映先前学到的知识,也可超出所学知识。“过渡性问题”的创设要因材施教,能够充分调动儿童的主动性,激发他们参与学习和深层的思考。儿童新知的获得是旧知的一种替代,也是对先前知识的提炼,在“过渡性问题”的缓冲中顺利达标。
(江苏省宝应县实验小学 225800)

