“三角形稳定性”的本质及其变教为学的方法

翟琬平 郜舒竹

“三角形的稳定性”在小学阶段属于“认识三角形”中的一个内容。在人教版教科书中，这一内容安排在四年级下册。这一内容的教学通常是通过“拉一拉”的活动，引导学生得到“三角形拉不动，具有稳定性；四边形可以拉动，不具有稳定性”的结论。这样的教学其实并没有反映出“稳定”的数学意义。

一、“三角形稳定性”的本质

“稳定”的本义是“不易倾倒”，英译为“stability”，比如照相机三脚架能够稳定地立在地面上，其数学原理是三点能够确定一个平面。这一含义并不是三角形稳定性中“稳定”的含义。三角形稳定性中的“稳定”英译为“rigidity”或“rigid”，其本义是“坚固”，表达的是“不易变形”的意思，与“柔韧（flexibility）”或者“易变形”相对。在力学中被看作物体在外力的作用下其形状和大小绝对不变，[1]在几何学中表达的是图形的形状和大小不变。

1979年，L. Asimow和B. Roth在《American Mathematical Society》杂志上发表的一篇题为“图形的稳定性（The Rigidity of Graphs）”的文章，其中对怎样的图形具有稳定性作出了详细解说：我们将一个图形看作是由顶点和边组成的集合，如果这个图形中的每两条连续的边，起始于点P，终止于点Q，且这两条边的长度保持不变（如图1所示），那么就说这个图形是稳定的。[2]也就是说，由一个顶点和两条边组成的角，由于边可随意旋转，角的大小也就可以任意改变。如用第三条边固定PQ的长度，那么角的大小就被固定了。构成的三角形的三个角都被固定后，其形状、大小自然不会再改变。而其他多边形，由于角度可以变化，其形状也随之变化，因此，这个图形就不稳定。

那么，如图2所示，在任意△ABC中，保证三边长度不变，三个顶点分别被三边固定，形状和大小不能改变，符合图形稳定的标准，所以三角形是稳定的。

在A. García的一篇关于二维图形稳定性的文章中，对如何判定图形是否具有稳定性进行了进一步阐释：若图形具有稳定性，它必须由Laman图组成。Laman图是指：在平面内，一类最小的具有稳定性的图形，其边和顶点的关系是，若有n个顶点，则必须有2n-3条边。若n≥3，图形的每两条边都要相连。[3]通过计算可以得出三角形的顶点与边的个数及结构都符合Laman图的定义，所以三角形是稳定的。四边形若要稳定，要有4×2-3=5条线段，为使每两条边都相连，需要在其对角线处加一条边，变成两个三角形。同理，五边形、六边形均需要添加边的条数才可以稳定（如图3所示）。

二、与相关知识的联系

“三角形的稳定性”在人教版教科书中位于四年级下册第三单元第二课，是学生学习了三角形的相关概念后的第一个内容。在学习之前，学生已经对角、三角形、四边形和图形的运动（主要是旋转）有了初步认识，在四年级上册中了解到平行四边形易变形，为突出三角形不易变形做铺垫。但在四年级上册介绍梯形的时候，用梯子、隔离墩这些看似十分稳定的实物为例引入梯形的概念，易使学生产生梯形同样具有稳定性的误解，在教学中教师应当注意到这一点。

“三角形的稳定性”不仅是三角形的特性之一，其本质更与初中将要学习的全等三角形有着紧密的联系。虽然小学生无需掌握全等三角形的知识，但作为教师，要明确二者之间的关系，并将全等三角形的知识渗透在教学过程之中。据史料记载，第一个应用全等三角形的人是古希腊时期的泰勒斯。他证明了第一个全等三角形的判定定理：若一个三角形有两角、一边分别与另一个三角形的对应角和对应边相等，则这两个三角形全等。[4]三百年后，欧几里得在其著作《原本》中对三角形的全等进行了整理，其中，公理4为“彼此重合的物体是全等的”；命题4、8、26提出了全等三角形的三种判定方法，即角边角、边边边、角角边。[5]其中“边边边”的判定方法与三角形的稳定性其实就是一码事，即如果三角形的三条边的长度固定不变，那么三角形的形状和大小也随之确定。

三角形的稳定性在建筑学中的应用众所周知。除此之外，在外交战略中也大有用处。利用三角稳定原理处理外交事务的基本思路是：如果要建立和维持稳定，则要努力构建三角关系。如果要打破稳定、防止稳定，则要主动破坏或制止建立三角关系。[6]

三、教学设计

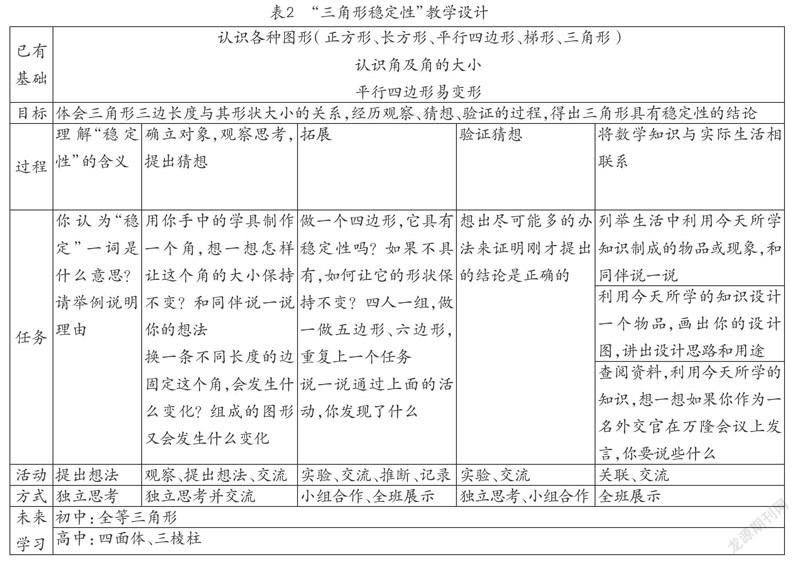
“三角形的稳定性”是三角形所具有的客观属性，属于规律性知识。学习目标可以确定为“了解三角形三条边的长度确定，三角形的形状、大小不变”。为了达到这样的目的，可以设计如下的学习任务和学习活动，让学生经历“观察、猜想、验证、应用”的学习活动，在活动中逐步认识三角形的稳定性。

第一是理解“稳定性”的概念。人教版教科书中缺少对稳定性的解释，且上文提到四年级上册中有从看似稳定的物品中抽象出梯形的内容，学生很难将“稳定”与“形状不变”联系起来。所以第一个活动设计为：你认为“稳定”一词是什么意思，请举例说明。帮助学生理解固定不变即稳定。期间可以引导学生思考：“图形的稳定指的是什么？”让学生认识到图形的稳定指的是形状、大小不变，为之后的探究做铺垫。这一环节，学生需要根据自身经验，提出想法（Inferring），从实际生活中抽象出稳定的概念。

第二是通过操作，理解角的对边固定角的大小，进而了解三角形三边的长度确定三角形的形状、大小，提出猜想。在《Mathematics for Junior High School》一书中用角的全等引入三角形的全等，[7]且上文中图形稳定性定义中的“两条连续的边”可以看作一个角。受此启发，探索、发现三角形稳定性的过程可以由角来引入，提出与“用你手中的学具制作一个角，想一想怎样让这个角的大小保持不变？这样做会出现一个怎样的新图形？”类似的问题，帮助学生确立观察对象，由固定角的大小引出三角形。再通过如“换一条不同长度的边固定这个角，会发生什么变化？组成的图形又会发生什么变化？”“四人一组，说一说通过上面的活动，你发现了什么？”这样的任务让学生在操作中体验三角形三边的长度与其形状大小的关系，与第一个环节中“稳定”的概念相联系，通过组内交流，提出三角形具有稳定性的猜想。

此外，上文提到四边形、五边形、六边形的形状和大小均需要添加辅助线，变成几个三角形后才能保持不变，布置诸如“用你手中的学具做一个四边形，它的形状会任意改变吗？如果会，如何让它的形状保持不变？做一做五边形、六边形，重复上一个任务”的任务，让学生体验需将多边形分割成若干个三角形才能稳定，进一步体会三角形具有稳定性。第二环节，学生需要经历的活动是观察（Observing）学具的变化，发现三角形边与角、边与形的关系；提出想法（Inferring）并相互交流（Communicating）。

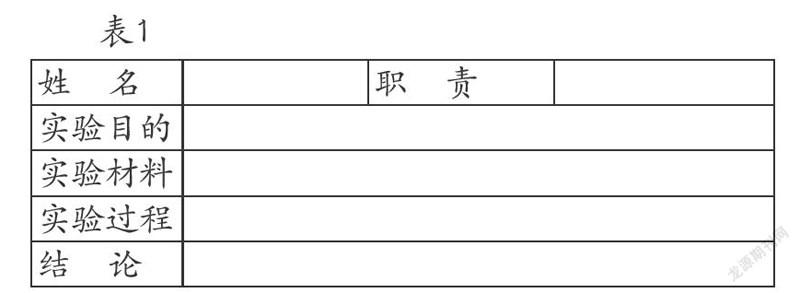
第三是验证猜想，得出使三角形稳定的条件，回应学习目标。通过完成上一环节的任务，学生已经认识到如果三角形三边的长度确定，这个三角形就唯一确定。本环节就要充分给学生时间去验证自己的结论。由于三角形稳定性的本质与全等三角形的判定密切相关，学生在初中还要进一步学习全等三角形的判定定理，在这一环节中应尽可能地鼓励学生发现更多的使得三角形稳定的条件，为升入中学后的学习打下基础。学生经历的活动是通过实验（Experimenting），整合信息，验证猜想，并记录（Recording）实验过程、观察发现的结论（记录单见表1）。与全班同学进行交流（Communicating），最终基于观察、经验、思考作出判断（Judgment）。教师在组织学生进行小组合作的时候，应明确要求和纪律，帮助小组长分好工，让每个小组成员都有作出贡献的机会。

结论

第四是对三角形稳定性的应用。由于每个学生的学习能力不同，在应用环节应进行分层设计，使不同程度的学生都能得到发展。针对学习能力较弱的学生，设计诸如“列举生活中利用三角形稳定性制成的物品”的活动。针对中等水平的学生，设计类似“利用三角形的稳定性设计一个物品，画出你的设计图，讲出设计思路和用途”的开放性活动。针对程度较好的学生，利用三角形稳定性的本质与外交策略的联系，将其他学科的知识融入其中，设计更加开放的活动。例如，今年恰逢万隆会议举办60周年，这个会议在历史上有重要的地位，让学生分小组查阅资料，利用今天所学的知识，想一想作为一名外交官在万隆会议上发言，将如何分析我国的外交策略？这个任务也可聚焦为分析中美俄三大国关系。作业的层次可以全部由学生自主选择，也可以由教师根据学生本节课的整体接受程度和资源配备情况来确定其中的两个任务，再由学生选择一个完成。这一环节学生经历的活动因任务的不同而不同，最好能作为作业让学生利用课余时间完成，再利用一节课的时间进行汇报。

以上设计可以用表格（见表2）清晰地呈现出来。

在三角形稳定性教学中，教师要使学习活动既符合学生的认知规律又符合数学本质，并且让学生的观察、操作等学习活动与数学知识之间建立关联，从而使学生正确掌握三角形的稳定性的概念。综观本节课的设计，将更多的时间留给了学生，让学生经历发现的过程。通过本节课的学习，使学生在知识方面，理解了三角形三条边的长度确定，三角形的形状、大小不变，并对全等三角形的判定定理有了初步认识。在个人能力方面，小组合作时既有分工又有共同探究，提高学生的沟通、协作能力。最后环节学生可以根据自己的学习程度和意愿自由选择作业，尊重、信任学生，锻炼自主能力；选择“外交官”作业的学生要查阅资料、深入思考，提出自己的见解，锻炼了学生进行批判性思维的能力。

需要指出的是，任何知识的教学方法不可能是唯一确定的。教师需要针对自己所教学生的实际情况，选择或者设计最适合学生学习的方法。

参考文献：

[1] 王同亿，主编译.英汉辞海下册[S].北京：国防工业出版社，2000.

[2] L. Asimow ， B.Roth. The Rigidity of Graphs[J]. American Mathematical Society，1979.

[3] A. García ， J. Tejel. Augmenting the Rigidity of a Graph in R2[J]. Springer Science and Business Media， 2009（3）.

[4] 徐传胜.全等三角形判定的历史追溯[J].中学生数理化，2014（7-8）.

[5] 欧几里得著.兰纪正，朱恩宽，译.几何原本[M].西安：陕西科学技术出版社，2003.

[6] 吴殿廷，等.三角稳定原理与中国的外交策略[J]. 北京师范大学学报（自然科学版），2015（2）.

[7] Anderson R. D. Mathematics for Junior High School（Volume 2）[M]. Yale University Press， 1960.

（首都师范大学初等教育学院 100048）