初中数学课堂有效提问的探索与思考

熊方亮

摘要：问题是开启学生思维，促进学习有效学习的重要手段。综观当前课堂教学现状，课堂提问华而不实，流于形式，效果不佳，难以充分调动学生，促进学生综合发展。因此，在初中数学课堂教学中，教师要不断思考与探索，优选有效方法，做到有效提问，从而构建高效灵动课堂。对此，笔者结合自身教学实践，对初中数学课堂有效提问提出了自己的几点建议，以作抛砖引玉。

关键词：初中数学；课堂提问；有效性

中图分类号：G633.6文献标识码：A 文章编号：1992-7711（2015）15-060-2

一、关注实际，有效提问

课堂提问是服务于教学内容与教学目标的，在进行问题设计时，教师要关注实际，灵活有效提问，以明确学习目标，启迪学生积极思维，培养学生问题意识。

首先，要注意问题的指向性，明确提问目标。教师要充分关注学生实际情况，从学生已有知识经验出发，围绕教学目标，紧扣教学内容，灵活提问。

比如，学习苏科版七年级上《合并同类项》后，在进行课后小结时，教师不应按照常规提问：“同学们，我们今天探讨了什么内容？你学到了什么？”这样的问题范围太广，目标性过大，有的学生思维如脱缰野马，一放不可收拾，有的学生却无从回答。倘若教师规定或限定范围，将问题空间与目标合理缩小，更有助于启迪孩子思维，唤醒学生知识与经验。

如判断下列各组中的两项是不是同类项？为什么？①02x2y与2x2y；②4abc与4ac；③2m2n与2mn2；④-125与12；然后提问：同类项的分类需要注意什么事项？这样，问题更有指向性，更能诱导学生快速思考。学生口答后总结三条注意事项：①两个相同：字母相同，相同字母的指数相等；②两个无关：与系数无关，与字母顺序无关；③所有的常数项都是同类项。

其次，要注意提问的思维性，激活学生思维潜能。在课堂教学中，有些教师单纯为活跃气氛，或看低学生能力，而提出大量欠缺思维性的问题，学生看似配合答问，但没有得到思维发展。

因此，在初中数学教学中，课堂提问要有思维深度，紧扣知识重难点或疑点，并考虑学生实际与现实生活，巧设开放性、适宜的、新颖的、有坡度的问题与情境，驱动学生思考，使其以原有知识与经验为基础进行主动建构，提高教学有效性。

二、尊重差异，分层提问

学生个体之间存在一定的差异，因此，教师在进行提问的过程中，要充分考虑学生的个性差异，尊重学生个体差异，结合学生学习基础、学习能力以及思维水平的不同，巧设层次性的问题，做到因材施教，分层提问，尽可能让每位学生都有所收获、有所提高、有所发展，从而增强学生学习信心。需注意的是，教师在设计分层问题时，要把握好问题的难度和梯度，问题难度既不可太大，否则部分学生无从入手，惘然无所得，也不可太浅显，否则难以启发学生思维，而应有针对性的、有层次性的提问，由浅入深，由易至难，循序渐进，层层递进，以促使学生主动参与答问，积极思索起来，促进学生的共同发展。

譬如，学习苏科版七年级下《因式分解》后，笔者结合学生实际水平和认知规律，设计了以下分层问题：

A组：把下列各式因式分解：（1）3ax2-3ay4（2）-2xy-x2-y2（3）3ax2+6axy+3ay2

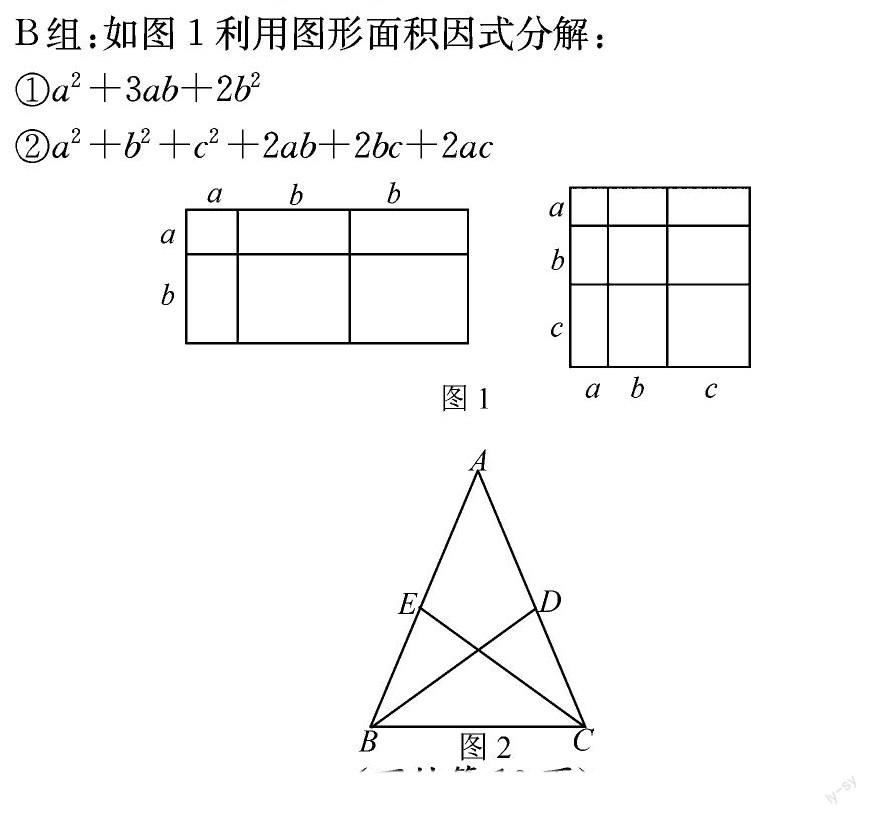
B组：如图1利用图形面积因式分解：

①a2+3ab+2b2

②a2+b2+c2+2ab+2bc+2ac

C组：①请你从下列各式中，任意选择两式作差，

并将得到的结果因式分解：9a2，（x+y）2，1，4b2；

②请写出一个三项式，使它能先提公因式，再运用公式法来因式分解，你编的三项式是，分解因式的结果是。

其中A组为基础性问题，B组为提升性问题，C组为拓展性问题，然后要求学生根据自身学习情况自主选择问题，进行参与作答，以满足不同层次学生的学习需求，让学生体验成功的喜悦，增强学生学习自信心。

三、变换角度，发散提问

发散性思维是学生要具备的思维品质之一，是培养学生创新能力的重要途径。教学实践表明，学生数学思维能力灵活与否与学生的发散性思维有着紧密联系。学生在解决问题的过程中，往往容易受思维定势的影响，拘泥于既定方法与模式，因而无法使问题得到高效解决。因此，在初中数学课堂提问中，教师要注意打破定势思维，变换问题角度，发散提问，从而促使学生多角度、多方位探索问题、分析问题、解决问题，培养学生思维的发散性、灵活性以及敏捷性，增强学生多向思维能力。如，教师在进行概念、法则、定义、公式、定理教学时，可以从不同的角度提出问题，引导学生多层次、多方位的去理解和运用；在进行习题教学时，可以通过一题多解，一题多变，一题多问等方式，训练学生多向思维能力，提高学生解题能力。

例如，苏教版八年级上P29例2经济习题中，笔者通过设置发散性问题，通过一题多问，培养学生思维发散性和灵活性，提高学生多角度、多方面思考、分析、解决问题能力。

例1：如图2所示，在△ABC中，已知AB=AC，两条角平分线BD、CE交于点O，请问：OB与OC是否相等？请说明理由。

变式1：若此题条件保持不变，请问OD与OE是否相等？BD与CE是否相等？为什么？

变式2：若此题中条件AB=AC保持不变，BD、CE分别为AC、AB上的中线，则OB与OC是否相等？OD与OE是否相等？BD与CE是否相等？请说明理由。

变式3：若此题中AB=AC这一条件仍保持不变，BD、CE分别为AC、AB上的高，则是否存在以下关系：OB=OC，OD=OE，BD=CE？请说明理由。

四、适时等待，深度回答

在课堂教学中，有些教师太过关注教学进度，急于得到正确答案或结论，因而学生答问时教师等候时间较少。如提问后，往往是“一问即答”，当某位同学答题受阻或回答没有接近预期答案时，便急着转问他人，转问无果时，老师干脆自圆其说、自问自答。在如此情况下，课堂提问又如何能发挥真正教育意义与作用，怎会促进学生思维发展，培养学生科学素质，甚至还会影响学生学习积极性。

事实上，在教学过程中，等待也是一种艺术，合理而恰当的等待，给学生充足思考时间，促使学生深入思考、主动探寻，形成意想不到的、令人惊叹的精彩回答，获得自豪感，提高学生学习兴趣。反之，学生基础再好，若欠缺思考时间，也难以快速形成有深度的回答。因此，在初中数学课堂提问中，教师要注意等待艺术，留出充足的等待时间，让课堂绽放出灿烂的智慧火花，促进有效提问。

如：教学苏科版七年级下《探索平行线的性质》时，笔者创设情境，提问引思：

如图3，工人在修一条高速公路时在前方遇到一座高山，为了降低施工难度，工程师决定绕过这座山，如果第一个弯是左拐30°，那么第二个弯应朝什么方向，才能不改变原来的方向。

问题一出，教师并没有急着让学生回答，而是在等待，让学生认真观察、自主探究、小组合作、交流讨论，主动获取新知。另外，在学生答问时，教师也要给其留出一定组织语言与调整答案的时间，并耐心聆听，灵活启发。

总之，课堂提问是一门艺术，也是一种智慧，它对于调动学生探究动机，激活学生思维，提高学生学习能力有着积极的作用。在平时教学过程中，教师要充分结合课程特点、学生心理特征以及认知规律，围绕教学目标，优化问题设计，从而启迪学生智慧，碰撞学生思维，让学生爱学、乐学，使课堂走向有效、高效。

（本文为江苏省“十一五”规划课题：农村初中数学课堂中主体参与探究的实践研究（编号：D/2013/02/625）阶段成果。）