关于提高排队效率的数学分析

任意

【摘要】 排队是社会不可缺少的规则，但排队往往耽误人们太多时间，给人们带来了不少烦恼，本文就这样一种社会现象进行数学分析及建立有关模型，探究如何使排队效率更高，来节约更多时间。

【关键词】 排队 队列设计 效率

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2015）04-091-01

0

一、问题提出

现在，我们几乎去哪里都要排队，去游乐园玩游戏设施、吃饭、看电影等等，排队这一项规则已经深入人心，但因为排队人数过多，时间过长，人们往往选择放弃，导致顾客的需求没有满足。如果节省了排队的大部分时间，顾客就可以提前办完事情，可以提前回家做自己想做的事情或者准备今后的事情，可见，减少排队时间不仅可以使人们有更加充裕的时间去做别的事情，还可以准备未来的事情，这使人们一整天做事的效率都提高了不少，所以，减少排队时间刻不容缓。那么，我们如何提高排队效率，减少排队时间呢？下面就让我们对这个问题开展模型建立。

二、问题分析

排队的问题和很多因素有关，以电影院为例，例如人流速度，服务速度，人数，影院设施，开放窗口个数等，依照常识来讲，开放窗口越多，排队效率就越高，但是窗口增多，人力物力也随之增多，所以我们也只能适当地控制窗口数量，根据我平时买电影票的经验，平均每人购票时间为1分钟，但买票时也难免会有些人与服务人员发生价钱上的争执，或者因为其他原因延长了时间，这些人平均10个人里才会有一个，而他们的平均购票时间是4分钟，但是这些人会延长他们所在的一整条队列的时间，导致那一队的人比其他队列慢，这样会有些不公平，所以我们可以重新设计队列。

三、模型假设

为了简化模型，我们假设每人购票时间为一分钟，那些延长购票时间的人购票时间为4分钟，其他特别因素均不对此产生影响。

四、模型建立

现在排队模型基本为图一所示：

其中“入1-入5”为人流，1、2、3、4、5为服务窗口，假设一般顾客为P1，耗时购票顾客为P2，假设5个窗口各有10人

假设1：P2在每队有且只有一人，则全部人购票完毕时间为4+9=13分钟，这时排队效率达到最理想。

假设2：P2在其中一队有2人，其余队P2随机分布且单队不超过两人，则这50个人全部买完票需4+4+8=16分钟。

假设三：其中一队P2有三人，其余队P2随机分布，则这50人买完票所需时间为4+4+4+7=19分钟。

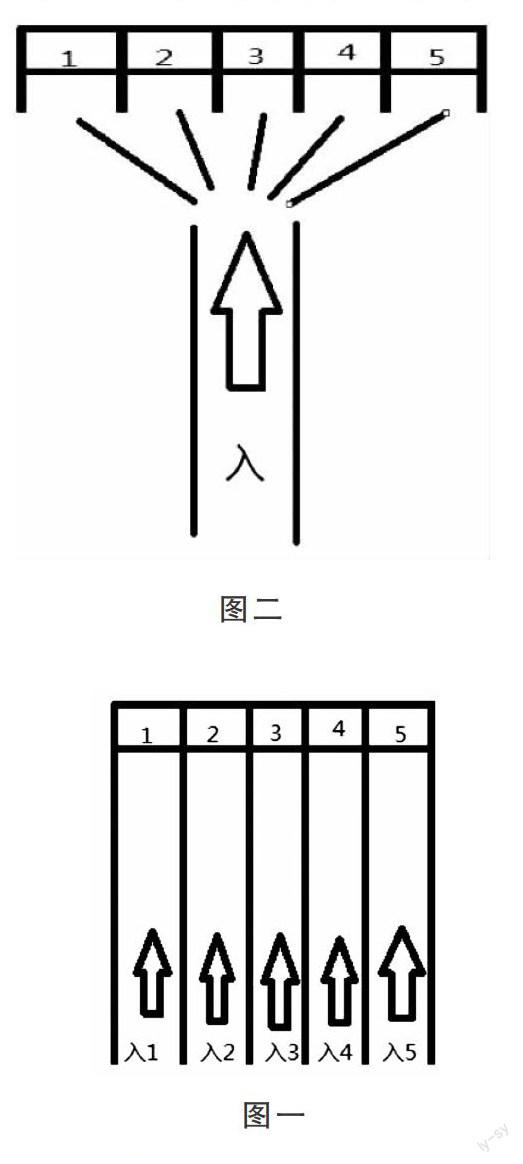
以此类推，排队效率最低的为25分钟，这样对P2最多的队列，第一个P2以后的人都不公平。所以，我根据排队论，设计了一个新的队列模型，如图二：

这样，所有人都排成一队，P1、P2都包括在内，当其中一窗口服务完毕，下一个排队的人立即上前买票，这样可以保证每一窗口都在服务，大大提高了效率。

假设1：最后的P2与最后几个P1同时买完票或所有P2在所有P1买完票之前买完，则时间与之前假设1所需的一样，为13分钟，这样依然为最理想。

假设2：最后一个P2买票时后面无人排队，即最后一个P2为这50人中最后一批入场买票时，排队时间最不理想，时间要在最理想的基础上再加上3分钟，即为16分钟。

图二所示的队列，所需所有可能的时间为13、14、15、16分钟，而图一所示的队列所需所有可能的时间为13、16、19、22、25分钟，由这几个数据可知，图二的队列排队所需平均时间小于图一的，且图二的队列人们等候的时间是公平的。

综上所述，图二所示的队列排队效率有显著提高。

五、模型的优缺点

优点：此模型适用于多种情形，如饭堂排队，银行排队等，不止适用于电影院购票，其他购票情况皆可。

缺点：因为每天到影院购票的人数都不一样，人流速度会有较大的偏差，而且不能保证每个购票窗口的服务速度都一致，且每条队伍的排队人数不尽相同，这就要通过假设或调查大概估算，所以与实际还是有一些偏差。

（指导老师：苏菊香）