基于改进张力补偿法的网状天线张力设计*

宗亚雳，张 功

(西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071)

基于改进张力补偿法的网状天线张力设计*

宗亚雳，张 功

(西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071)

大型网状反射面天线是结构复杂、柔性索和梁单元众多的高度几何非线性结构，天线内部索单元的真实张力不易控制，文中针对该问题提出了一种基于改进张力补偿法的索网张力优化设计方法。首先，借鉴模拟预应力空间结构施工的张力补偿法的思想来设计环形桁架可展开天线的索网张力和网面放样状态，但是对借鉴该思想设计的结构进行的非线性静力分析不易收敛，为此将小弹性模量技术应用于张力补偿法，形成改进的张力补偿法；然后，基于改进的张力补偿法，提出了网面张力和网面放样状态的优化设计模型。数值仿真结果表明，该算法有效地改善了网状天线非线性静力分析的不收敛现象，能有效控制主动索的真实张力，且网面放样状态形状规则，易于工程实现。

网状反射面天线；改进的张力补偿法；小弹性模量技术；网面真实张力；放样状态；优化设计模型

引 言

网状可展开反射面天线因其口径适用范围广、收纳率大、质量轻等优点而得到越来越广泛的应用[1-5]。欲使网状可展开天线具有一定的形状精度，必须对其索网结构施加相应的张力。网状可展开天线展开到位后，在索网预张力的作用下达到平衡位置，形成天线所需型面。因此，需要设计一组合适的索网预张力，使天线在平衡位置既满足型面精度要求，又满足索拉力大小的需求。

对于上述问题，文献[6]～[8]以天线纯索网的节点力平衡方程为基础，采用奇异值分解法或极小范数法进行求解。对于纯索网结构，采用该方法设计的张力为一组平衡力系，但是经天线整体“自平衡”后的索网张力与设计值不能完全一致，甚至设计的张力不能保证天线的型面精度。文献[9]～[11]以天线整体的有限元位移平衡方程为基础，结合优化算法来设计满足天线型面精度的索网拉力。文献[12]和[13]将上述2类方法结合起来，首先以内部索网的节点力平衡方程为基础设计内部纯索网的拉力，然后再以边界索和桁架结构的位移平衡方程为基础，结合优化算法设计边界索的拉力来保证内部索网的边界条件不变。文献[9]～[13]的算法可以将索网和桁架之间的相互影响考虑在内，但采用该方法设计的“张力”仅是天线结构“平衡前”的张力值，对天线整体结构的索网真实张力不可控。这是因为索网中的真实张力完全由天线结构经“自平衡”后确定，由于天线结构复杂，采用该方法设计的“张力”的变化不足以有效控制真实张力的分布情况。

另一方面，未来可展开天线将朝着大口径、高频段方向发展，天线的复杂程度和索段的数目也将随之增加。上述索网张力设计方法主要关心天线的型面精度与索网张力大小是否满足要求，却忽略了施工的方便性，导致设计出的索段放样长度千差万别，无规律可循，这给索段的测量和索网的编织带来了极大的麻烦。当天线口径达几十米甚至上百米时，将有成千上万根索段，此时，网状天线的制造和装配将会成为一个耗时、耗资的大工程。

为解决上述问题，本文首先对网状天线上、下网面的放样状态进行了参数描述，并引入了模拟预应力空间结构施工的张力补偿法进行索网张力设计，确保索网张力的设计值为天线平衡后的真实张力。然后采用小弹性模量法来减小上、下网面之间的刚度耦合，改善对网状天线非线性静力分析时不收敛的现象，形成改进的张力补偿法。最后，以改进的张力补偿法为基础，选取合适的设计变量，以天线型面精度为目标，对索网预张力和上、下网面的放样状态参数进行优化设计。算例表明，该算法改善了对网状天线非线性静力分析时的不收敛现象，并能在满足天线精度要求的同时，有效控制网状可展开天线的真实预张力，且给出了放样状态下的网面形状，为网状可展开天线的设计和施工提供了参考依据。

1 张力补偿法

1.1 张力补偿法简介

张力补偿法提供了一种对索段张力予以有效控制的迭代方法，它最初由文献[14]针对索网结构的施工问题提出，目的是为了保证在施工后主动索的真实张力值达到设计水平。文献[15]将该方法推广应用于弦支穹顶结构的张力设计中。张力补偿法将结构中的索分为主动索和被动索，对主动索进行张拉，且施加张力有先后次序。

假设某混合结构中有n组主动索，张力设计目标值分别为Pi(i=1,2,…,n)。设张拉第i组主动索后，将前一组索张拉并固定后再进行后一组索的张拉，张拉完最后一组后将主动索固定，重新从第1组索开始张拉，直至所有主动索的真实张力均等于张力设计值。张力补偿法模拟施工过程的循环计算步骤见文献[14]。

1.2 基于张力补偿法的网状天线张力设计

本文借鉴上述思想，将环形桁架可展开天线的索结构分为主动索和被动索，设调节索为主动索，上、下网面的索为被动索。在用张力补偿法进行张力设计时，不再分别对n组调节索进行张拉，而是同时对n组调节索进行张拉。

假定在主动索未张拉之前，上、下网面的节点分别在理想曲面上，如图1所示，这样的理想曲面称为放样曲面。若该曲面为抛物面，则称为放样抛物面，放样抛物面的焦距为放样焦距。

图1 主动索张拉前天线结构示意图

图1所示为环形桁架天线简图，此时上、下网面已经挂接在环形桁架上，主动索尚未张拉。不考虑重力的影响，此时上、下网面处于零拉力状态，且上、下网面节点都在相应的放样抛物面上。

图2所示为装配好的天线示意图，图中虚线为网面的放样抛物面，实线为天线的工作抛物面。Fup、Fdown分别为上、下网面工作曲面的焦距。上、下网面之间为主动索，即调节索。

图2 主动索张拉后天线结构示意图

由上述放样抛物面的定义可知，天线上、下网面的放样状态可通过放样焦距进行参数化，且各索段在放样抛物面上分布规则，便于网面编织。

选取好主动索和被动索后，即可采用1.1节中的张力补偿过程进行网状可展开天线张力设计。由于天线桁架对索内力以及索内力之间的影响较复杂，给定的索网张力初值并不能使天线处于平衡状态[12]，因此必须进行非线性静力分析才能获得平衡状态以及索网的真实内力。但通过数值仿真发现，非线性静力分析收敛很慢，有时甚至发散，这可采用小弹性模量技术[16]来加以解决。

2 改进的张力补偿法

改进的张力补偿法为网状天线张力优化设计提供了一种新途径，并能保证张力真实值与设计值保持一致。这意味着张力真实值的大小可以由设计值直接、高效地控制。一般采用增量Newton-Raphson迭代法对网状天线进行非线性静力分析，但该迭代法对迭代初值要求较高。由于改进的张力补偿法假设的网面放样位置距离工作曲面较远，静力平衡分析不收敛现象经常出现，因此本文引入了小弹性模量技术来解决这一问题。

2.1 小弹性模量技术的应用

天线整体的非线性有限元方程可写为

Kτδ=N

(1)

式中：Kτ为整体切向刚度矩阵；δ为节点位移向量；N为节点不平衡力向量。且

Kτ=K+S

(2)

式中：K为线性刚度矩阵；S为预张力刚度矩阵。

引入小弹性模量技术后，在对网状可展开天线进行静力分析前，先假设主动索(调节索)具有很小的弹性模量，暂时减小其弹性刚度与被动索(上、下网面索)的弹性刚度耦合，仅考虑其预应力刚度。在实际计算时，给主动索施加较大的初应变并保证单元内力不变，即

Es,iAiεL,i=EiAiεi=Pi

(3)

式中：Pi为给定的第i根主动索的预拉力；Es,i为所定义的第i根主动索的小弹性模量；Ai为相应主动索的横截面积；εL,i为相应主动索的大初始应变；Ei、Ai和εi分别为第i根主动索的真实弹性模量、横截面积和初应变。

被动索单元的线性刚度矩阵为

(4)

式中：i为索单元编号;j、k为与第i个索单元相连的节点编号;Li为第i根索的长度。结合式(3)可得主动索单元的线性刚度矩阵：

(5)

式中:j和k分别为与第i个竖向索单元相连的上网面节点编号和下网面节点编号。由于实际εi远小于εL,i，因此

(6)

索单元预应力刚度矩阵为

(7)

节点不平衡力向量为

(8)

式中，C(j)为与节点j相连的索单元编号的集合。

通过组装单元线性刚度矩阵、单元预应力刚度矩阵和节点不平衡力向量，可得天线整体的非线性有限元方程。图3为网状天线的一个主动索单元示意图。

图3 主动索单元示意图

图3中主动索单元i通过上、下网面上的节点j和k与多个索单元相连。单元i在整体刚度矩阵中对应的有限元方程为

(9)

式中：U(j)为与节点j相连的上层被动索单元编号的集合；D(k)为与节点k相连的下层被动索单元编号的集合；uj为杆单元u除节点j外的另一节点编号；dk为杆单元d除节点k外的另一节点编号；δj、δuj、δk和δdk分别为节点j、节点uj、节点k和节点dk的位移。结合式(6)可得：

(10)

对于尼龙、芳纶纤维等绳索材料，其预应力刚度一般远远小于其线性刚度，由式(10)可知，小弹性模量技术将上、下网面节点间的位移耦合项弱化，使得位移耦合项仅与较小的主动索的预应力刚度矩阵有关。

2.2 改进张力补偿法的迭代步骤

设某环形桁架可展开天线共有m个索单元，其中调节索有n个，P*为索单元张力的目标值。引入小弹性模量技术后，改进张力补偿法的计算步骤如下：

1)给主动索单元施加很大的初始应变εL,i(k)，调节索(主动索)的单元编号i=1,2,3,…,n，给上网面和下网面索单元施加零应变，令循环计算序号k=1。

2)给定主动索小弹性模量Es,i，上、下网面索单元的真实弹性模量为Ei。

5)若ΔFi(k)满足收敛条件，迭代停止，转步骤6。否则，令第k次循环中计算得到的第i根主动索的张力控制值推出的应变值εL,i=Ci(k)/(Es,iAi)，k=k+1，返回步骤2。

6)根据此时平衡状态对应的节点坐标和周边桁架的应力更新有限元模型，恢复主动索单元弹性模量E，对索单元施加预应变εf,j=Fj(k)/(EjAj)，j=1,2,3,…,m(εf,j为最终第j根主动索的真实应变，Fj(k)为迭代停止后第j根索单元的真实张力值)，得到新的有限元模型。

7)非线性有限元静力分析后得到索单元的实际内力FR。

由上述迭代过程可知，P*≈F，F为恢复真实弹性模量后主动索的真实张力向量，而F≈FR，因此P*≈FR。这意味着天线中主动索的真实张力可由期望的目标值来直接控制。这是因为若不考虑计算误差，平衡构型下的有限元方程为

(11)

式中：Keq和Seq分别为平衡构型下天线的整体弹性刚度矩阵和预应力刚度矩阵；Neq为平衡构型下的节点不平衡力。根据平衡构型对应的节点坐标和周边桁架的应力更新有限元模型，将材料的弹性模量恢复为真实值，同时对索单元施加预应变得

(12)

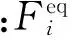
[(Keq+Seq)+(Ka+Sa)]δ=N

(13)

式中，Ka和Sa为恢复主动索的真实弹性模量后增加的主动索的弹性刚度矩阵和预应力刚度矩阵。

由于恢复真实弹性模量前后，天线结构内的应力状态保持不变，受载荷的节点位置也没有发生变化，因此平衡力系没有被破坏，此时式(13)中不平衡力N=Neq=0，式(13)可写为

[(Keq+Seq)+(Ka+Sa)]δ=0

(14)

由于矩阵(Keq+Seq)+(Ka+Sa)非奇异，所以δ=0。可见，当不考虑计算误差时，在恢复真实弹性模量前后，结构的构型和预张力基本不发生变化。因此可认为P*≈FR。

3 张力和放样状态的优化设计

对网状天线结构来说，网面精度是最重要的设计指标之一。由图1可知，网面精度除与调节索的张力有关外，还与上、下网面的放样尺寸有关。为了减少设计变量数目，特将上、下网面的放样尺寸以其放样焦距表示，即通过设计上、下网面的放样焦距fup、fdown来设计上、下网面索单元的原长，从而达到设计网面张力的目的。

3.1 网面零拉力状态的确定

设天线高度为H，口径为D，上、下放样抛物面的焦距分别为fup、fdown，坐标原点在上网面的中心。

索单元的原长可以通过下式求得：

(15)

式中，i，k为该索单元的2个节点，xi,xk,yi,yk,zi,zk分别为i、k节点的x，y，z坐标。

式(15)中的zi和zk可由上、下网面的放样焦距fup、fdown表示为

(16)

因此可通过设计fup、fdown来设计网面上索单元的原长，从而实现上、下网面放样状态的设计。

3.2 网面零拉力状态的确定

结合图2给出的天线示意图，可建立以下优化模型来设计索网体系的预张力和网面放样状态。

hmin≤h≤hmax

(17)

设计变量：

fup，fdown：上、下网面的放样焦距。

目标函数：

(18)

约束条件：

除设计变量的上、下限约束外，还有上、下网面之间的距离约束hmin≤h≤hmax。天线高度H确定后，上、下网面之间的距离要适中。距离太小，会给后续的调整工作带来不便；距离太大，会导致下网面的张力过大，给天线展开到位造成困难。

设计变量中力的单位是N，而焦距的单位是m，存在量纲的差别，这可能导致迭代收敛困难。因此，首先将设计变量进行归一化处理。归一化处理后的约束为

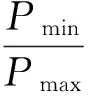
(19)

式中，Δ代表(up,down)。

图4为优化设计框图，图中虚线框内为张力补偿法迭代过程。给定优化设计变量初值后，将采用改进的张力补偿法对天线进行张拉，使竖向索的真实张力与设计值相等。此时一般rms不满足工程需求，需要通过优化获取合适的设计变量值，既使天线型面精度满足要求，又使张力满足要求。

图4 张力优化设计框图

4 算例分析

以某口径D=10 m、高度H=1.5 m、沿半径分段数为5段、上工作表面焦距Fup= 6m、工作频率为2 GHz的周边桁架可展开天线为例进行分析，如图5所示。要求天线型面精度小于3 mm(λ/50，λ为工作波长)，调节索拉力均不小于5 N，上、下网面之间的距离h不小于200 mm(以便于网面调整)。

图5 10 m口径周边桁架可展开天线

首先，给定放样焦距fup和fdown的初值分别为6.5 m和600 m，给所有调节索施加一个较大的初应变0.99，其余索单元的初应变为0。为了减小设计变量的数目，节省计算时间，本文将调节索分为6类，每一环调节索作为一类。图6为调节索的单元编号，表1为调节索的分类说明。表1中R1～R6为调节索的类别，给定所有调节索的初始张力设计值为6.88 N，依据式(17)进行优化。

图6 调节索编号

表1 调节索(主动索)分类

经过优化后，得到型面均方根误差为2.39 mm(<3 mm)，满足要求。优化后设计变量的最优值和上、下网面之间距离h的值见表2。可见拉力的最小值为5.00 N，h为213.81 mm，均满足要求。图7、图8和图9分别为rms、张力设计值和放样焦距随优化迭代次数变化的变化曲线。

表2 优化结果

图7 rms变化曲线

图8 张力设计值变化曲线

图9 放样焦距变化曲线

从图8可知，R1组的竖向索拉力最大，且拉力从R1到R6逐渐减小。这说明将放样抛物面拉至工作抛物面，需要中心竖向索的拉力较大，边缘竖向索的拉力较小。

表3为各类调节索的真实张力设计值以及各环调节索真实张力与设计值的最大偏差。最大偏差为-0.140 0%，约0.014 7 N，可以认为设计的真实张力值达到了目标值。由表3可知，基于改进张力补偿法的网状天线张力设计方法可有效地控制天线“自平衡”后的真实张力。

表3 各环调节索的拉力值

依据设计好的调节索的真实张力及其伸长后的长度，通过式(20)计算出竖向索的原长，以指导索网放样加工。

(20)

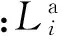
5 结束语

本文通过理论推导、方法推导与数值仿真，得出如下结论：

1)借鉴张力补偿法的思想，将索网分为主动索和被动索，应用迭代算法有效地控制了天线“自平衡”后主动索的真实张力。

2)采用小弹性模量技术对张力补偿法进行修正，减小了主动索弹性刚度与被动索(上、下网面索)弹性刚度的耦合程度，改善了非线性静力分析迭代的收敛特性，使得张力优化设计工作得以顺利进行。

3)对上、下网面的放样状态进行参数化描述，与传统方法相比，该方法大大减少了设计网面张力的设计变量数目。它只需给出放样焦距就能达到设计上、下网面放样状态的目的，且上、下网面零拉力状态下的节点坐标都在相应的理想抛物面上，放样状态规则，易于放样加工。

4)对主动索进行分类，减少了设计变量的数目，提高了设计效率，但如果对主动索的分类更细致一些，增加一些设计变量的数目，那么型面精度将得到进一步提升。此外，一般情况下，型面精度是通过保证索长精度来加以保证的，但网状天线具有小应变、大位移的特点，索长误差的累积会使型面精度无法得到保证。因此，还需进一步研究新的型面精度保证方法，比如可以在特制放样模具上编织放样抛物面等。

[1]SEMLERLD,TULINTSEFFA,SORRELLR,etal.Designintegrationanddeploymentoftheterrestar18-meterreflector[C]//The28thAIAAInternationalCommunicationsSatelliteSystemsConference.California,USA:AIAA, 2010.

[2]MIURAK,MIYAZAKIY.Conceptofthetensiontrussantenna[J].AIAAJournal, 1990, 28(6): 1098-1104.

[3]HIGUCHILK,KISHIMOTON,MEGUROA,etal.StructureofhighprecisionlargedeployablereflectorforspaceVLBI[C]//the50thAIAAStructures,StructuralDynamics,andMaterialsConference.California,USA:AIAA, 2009.

[4]THOMSONMW.TheAstromeshdeployablereflector[C]//TheIUTAM-IASSSymposiumonDeployableStructures:TheoryandApplications.Cambridge,UK:Springer, 1998.

[5]YOUZ,PELLEGRINOS.Cable-stiffenedpantographicdeployablestructurespart2:meshreflector[J].AIAAJournal, 1997, 35(8): 1348-1355.

[6]TIBERTAG.Optimaldesignoftensiontrussantennas[C]//The44thAIAA/ASME/AHS/ASCStructures,StructuralDynamicsandMaterialsConferenceandExhibit.Norfolk,USA:AIAA, 2003.

[7] 李刚，关富玲. 环形桁架展开天线索网的预拉力优化技术及其应用[J]. 固体力学学报, 2006, 27(S1): 174-179.

[8] 杨东武，仇原鹰，保宏, 等. 基于Moore-Penrose逆的索网天线预拉力设计方法[J]. 机械工程学报, 2012, 48(21): 22-27.

[9]DIJJ.Optimumdesignofcable-netdeployableantennawithstressandfrequencyconstraints[C]//The3rdInternationalSymposiumonSystemsandControlinAeronauticsandAstronautics(ISSCAA).Harbin,China:IEEE, 2010.

[10] 杨瑞. 索网式可展开天线的反射面找形及精度调整技术研究[D]. 西安: 西安电子科技大学, 2010.

[11] 狄杰建，段宝岩，罗英，等.大型网状可展开天线预张力的优化[J].华南理工大学学报: 自然科学版, 2004, 32(6): 23-26.

[12] 尤国强, 张杰. 可展开天线中索网结构的形态分析与设计[J]. 工程力学, 2012, 29(11): 306-312.

[13] MORTEROLLE S, MAURIN B, QUIRANT J, et al. Numerical form-finding of geotensoid tension truss for mesh reflector[J]. Acta Astronautica, 2012 (76): 154-163.

[14] 卓新. 张力补偿法及其在预应力空间结构中的应用[J]. 工业建筑, 2002(S): 310-316.

[15] 郭云, 陈志华. 改进的张力补偿法在弦支穹顶结构ANSYS程序分析中的应用[J]. 工业建筑, 2003(S): 343-347.

[16] THOMAS C J，BART-SMITH H. Finite element modeling and analysis of large pretensioned space structures[J]. Journal of Spacecraft and Rockets, 2007, 44(1)：183-193.

宗亚雳(1988-)，女，博士，主要研究方向为索网天线结构优化设计。

A Pretension Design Method of Large Deployable Mesh Reflectors Based on Advanced Tension Compensation Method

ZONG Ya-li，ZHANG Gong

(KeyLaboratoryofElectronicEquipmentStructureDesign,MinistryofEducation,XidianUniversity,Xi′an710071,China)

A large deployable mesh reflector consists of a great number of links and beams etc. Thus the real tension in the cables cannot be controlled efficiently by their initial tension. To overcome this, the tension compensation method (TCM), usually used to simulate the prestressing process of space network structures, is employed to design the pretension and zero-tension state of tension truss deployable reflectors. To overcome the static analysis unconvergence, TCM with the low Young′s modulus technique namely the advanced tension compensation method (ATCM)is presented. Then the mathematical optimization model for pretension and zero-tension state design with far fewer design variables is established based on ATCM. Numerical simulation results show that this method can improve the nonlinear static analysis unconvergence of the deployable mesh reflectors and can control the real tension in the net efficiently. Meanwhile, zero-stress state of the net is in a regular shape which is very convenient to construct.

deployable mesh reflectors; advanced tension compensation method (ATCM); low Young′s modulus technique; real cable tension; zero-stress state; optimization design model

2014-09-24

国家自然科学基金资助项目(51035006；51105290)

V443+.4

A

1008-5300(2015)01-0025-07