基于Adams的伞弹系统降落过程动力学仿真*

张 俊，曹 俊，陈 敏

(南京电子技术研究所， 江苏 南京 210039)

基于Adams的伞弹系统降落过程动力学仿真*

张 俊，曹 俊，陈 敏

(南京电子技术研究所， 江苏 南京 210039)

伞弹系统在自由下落过程中具有非常复杂的动力学特性，仿真模拟其运动规律对于其结构设计和稳定性研究具有指导意义。文中以末敏弹稳态扫描段为例，建立了旋转伞弹系统的运动模型，并给出了基于Adams软件的多体动力学仿真结果。最后，结合末敏弹的作用机理和弹箭目标的外弹道理论，分析了各弹道诸元随飞行时间的变化规律。研究成果可应用于伞弹系统的设计分析、指导伞弹空投试验。

伞弹系统；动力学模型；稳态扫描；末敏弹

引 言

降落伞是一种应用广泛的柔性气动力减速装置，涡环旋转伞作为其中一种重要类型，下落过程中伞衣高速旋转，使得伞弹系统具有良好的稳定性。此外，它还具有开伞动载小、阻力系数大等优点，因而被国内外广泛应用于飞行目标的弹道控制，如末敏弹的减速及姿态稳定等方面。

伞弹系统具有复杂的动力学特性，一直是多体动力学的研究热点和难点。文献[1]针对炮射末敏子弹的工作过程，应用凯恩法建立了伞弹系统刚柔耦合动力学模型，并应用Matlab程序进行了数值计算；文献[2]将降落伞、伞盘及子弹分别考虑为单个刚体，将伞绳的柔性、刚体之间的连接方式及力学约束考虑在内，建立了三刚体数学模型并进行了仿真计算；文献[3]借鉴现代控制理论的结构化建模方法，考虑了伞弹系统所经历的瞬态过程，建立了伞弹系统的自由坠落段、拉直段、充气段及稳定下落过程的结构化模型；文献[4]分别建立了单刚体、单质点及多刚体系统动力学模型，并深入分析了计算结果；文献[5]考虑了末敏弹在3个方向上的位移和1个横滚角的四自由度运动，建立了母弹飞行段、抛撒段、减速减旋段的弹道仿真模型，并提出了一种末敏弹外弹道计算的简便方法。

本文基于当前研究的基础，以末敏弹的稳态扫描弹道为研究对象，给出了基于Adams软件的多体动力学仿真方法，并分析了各弹道诸元的变化规律，研究方法与结果可为伞弹系统的弹道计算及可视化仿真奠定基础。

1 典型末敏弹的作用过程

末敏弹是一种由弹体、减速减旋装置、稳态扫描装置、伞弹连接装置、中央控制器、复合探测系统以及EFP战斗部组成的智能弹药[5]。当作为运载体的母弹飞行至预定目标上空后，末敏弹被抛射出来，在自由下落一定高度后，减速减旋装置弹出，在稳定弹体的同时，将其速度和转速按规定时间或距离降至有利于主旋转伞可靠张开条件。随即主旋转降落伞抛出，以稳定的落速和转速下落，并保证弹体纵轴与铅垂方向形成一定角度对地面进行螺旋式扫描。当弹上的复合探测系统搜索并识别目标后，起爆战斗部并毁伤目标。图1为典型末敏弹的全弹道作用过程。图2为末敏弹的主旋转降落伞完全充气张开后的几何模型，由子弹弹体、涡环旋转降落伞、伞绳、伞盘以及连接杆等组成，其中，涡环旋转降落伞由4片伞衣幅和32根不同长度的伞绳连接而成。伞衣幅上不对称的开口设计可以实现降落伞在充满气的情况下，整个降落伞系统形成一定的凸面和倾斜度，在下落过程中由于不对称空气动力和力矩的作用即可实现稳定旋转。

图1 典型末敏弹的全弹道作用过程

图2 末敏弹稳态扫描运动的几何模型

2 伞弹系统稳定下落过程的动力学模型

当降落伞充气胀满后，伞绳拉紧，此时，无论伞绳之间还是伞绳与伞盘之间的相对运动都很小，再加上伞衣上存在通气导旋气孔，使得伞衣幅的透气量增加，伞衣内外的大气压差和侧向力都将减小，这使得伞衣幅和伞绳均不易变形。在伞弹系统下落过程中，其空气阻力系数会发生变化，但是，由于其落伞较低，伞衣的气动参数基本上不受弹体尾流的影响[6]。根据以上分析，伞弹系统在稳态扫描阶段的运动中，可将降落伞与伞盘作为一个刚体，弹体作为另一个刚体，两刚体间采用柱铰联接方式。

旋转伞与弹体之间的连接关系如图3所示，其中：d点为伞弹连接点；o为弹体质心；p为降落伞质心；a为悬挂点至降落伞质心的距离；b为悬挂点至弹体质心的距离。

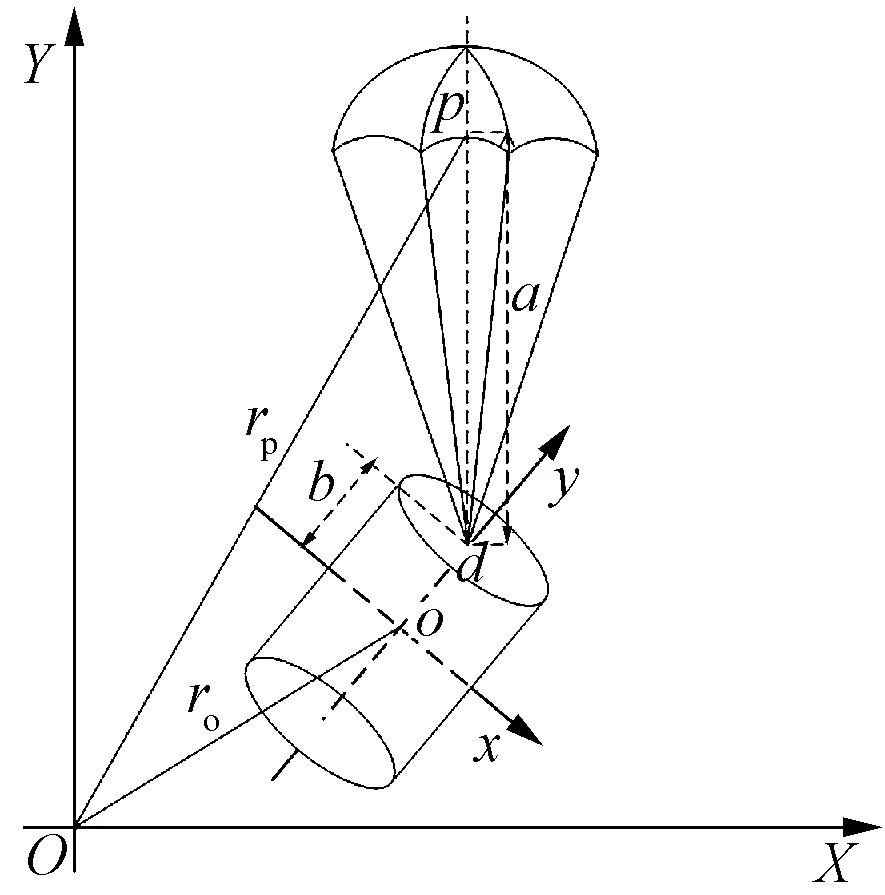
图3 涡环伞与弹体间的连接关系

在基准坐标系下，弹体质心径矢为ro，伞刚体的质心径矢为rp，则有：

(1)

将子弹受到的重力和空气阻力投影到弹体平动坐标系上，将子弹受到的外力矩投影到弹体固连坐标系上。在弹体平动坐标系中，根据牛顿第二定律建立弹体质心运动学方程组，在弹体固连坐标系下，应用动量矩定律，再加上子弹的速度与位移、角速度与欧拉角的运动学关系式，共同组成子弹的动力学方程组：

(2)

式中：Go为弹体重力；Rxo为空气阻力；Ryo为空气升力；mo为子弹质量；Jo为子弹的转动惯量；ωo为子弹转速；Mxzo为极阻尼力矩；Mzzo为赤道阻尼力矩；Ψo、θo、φo为欧拉角；xo、yo、zo为子弹质心位置坐标；vxo、vyo、vzo为3个方向上的子弹速度分量。

将降落伞受到的外力转换到降落伞的平动坐标系上，将外力矩转化到降落伞的固连坐标系上。分别应用牛顿第二定律和动量矩定律，再加上降落伞的速度与位移、角速度与欧拉角的运动学关系式，共同组成降落伞的动力学方程组：

(3)

式中：Gp为降落伞的重力；Rxp为空气阻力；Ryp为空气升力；mp为降落伞的质量；Jp为降落伞的转动惯量；ωp为降落伞的转速；Mxzp为极阻尼力矩；Mxwp为空气导转力矩；Mzzp为赤道阻尼力矩；Ψp、θp、φp为欧拉角；xp、yp、zp为降落伞质心位置坐标；vxp、vyp、vzp为3个方向上的降落伞速度分量。

3 基于Adams的多体动力学仿真

已知条件为：子弹质量为10.8 kg；子弹的静态悬挂角为22.5°；降落伞由一种特殊的涤纶材料制成，质量为0.12 kg；最大截面的直径为1.4 m；降落伞系统的特征长度为1.21 m；初始条件根据末敏子弹在减速减旋运动结束时的弹道参数确定。主旋转降落伞张开时所处的高度为350.5 m；子弹的初始速度为53.5 m/s，在3个方向上的分量为vox=9.3m/s，voy=-52.48m/s，voz=4.7 m/s；子弹的初始角速度分量为wox=0，woy=223.8rad/s，woz=0；降落伞系统的初始速度在3个方向上的分量为vpx=9.3 m/s，vpy=-52.48 m/s，vpz=4.7 m/s；初始角速度分量为wpx=0，wpy=223.8 rad/s，wpz=0，计算时间为20 s。

利用Adams软件进行多体动力学仿真，这种方法可直观地可视化其运动过程，并可通过分析系统中各部分的力学关系，不断改善模型仿真更为复杂的刚柔耦合多体动力学问题。导入几何模型后，设置已知参数和初始条件，伞弹之间采用铰联接约束条件。图4为部分弹道诸元的仿真结果，其中，图4(a)为子弹的下落高度随时间的变化规律，图4(b)为子弹的下落速度随时间的变化规律，图4(c)为子弹的旋转角速度随时间的变化规律，图4(d)为子弹的扫描角随时间的变化规律。

图4 部分弹道诸元的仿真结果

计算结果表明：末敏子弹的下落高度随时间基本呈线性变化；子弹的下落速度在张开主旋转降落伞后迅速降低，这是由于降落伞的空气阻力特征量较大，大约2 s后就与重力达到了平衡，从而使其铅垂方向上的加速度降为零，此时下落速度达到最小值，随后一直以恒定速度约11 m/s下落；子弹的旋转角速度和落速变化规律基本一致，即先迅速减小后趋于稳定，在3 s左右达到稳定角速度约23 rad/s，即转速约为3.65 r/s；转速的稳定比落速用时多约1 s，这是由于转速主要与伞弹系统的极阻尼力矩和导转力矩密切相关，而二者又和速度紧密联系，所以只有在下落速度达到稳定以后，转速才会逐渐达到稳定状态；子弹的扫描角在大幅波动5 s后，逐渐趋近于末敏子弹的静态悬挂角22.5°，这是由于子弹的初始摆动较为剧烈，当子弹的下落速度和旋转角速度稳定后，仍需要克服摆动所产生的惯性力，所以扫描角的稳定时间就要延长，约7 s后达到稳定状态，此时末敏子弹下落了约265 m。根据末敏子弹的落速、转速以及扫描角的计算结果得出：末敏子弹达到稳定状态所需时间较短，在进入稳定状态后，其下落速度、转速以及扫描角几乎没有变化，这是由于未考虑气动力参数随弹道诸元和外部环境因素不断变化的原因。

图5给出了末敏子弹在整个下落过程中的稳态扫描螺旋线。子弹的稳态扫描段是指在末敏子弹完成减速减旋运动后，打开主旋转降落伞，在主旋转伞的作用下，伞弹系统在空气阻力和重力作用下进一步减速，在空气导旋力矩和极阻尼力矩的作用下进一步减旋，最后达到稳态扫描的运动状态。在稳定状态下，伞弹系统一边以一定速度下落，一边以一定转速绕降落伞的铅垂轴旋转，由于子弹体轴线方向与铅垂方向成一定角度，因而末敏子弹能够实现螺旋式稳定扫描并探测装甲目标。通过这两个不同运动时间段形成的扫描轨迹线可以看出，在稳态扫描运动初期，由于子弹的落速、转速及扫描角没有达到稳定，所以形成的扫描轨迹也没有规律性，散布范围较大。随着末敏子弹的运动状态逐渐趋于稳定，其扫描轨迹逐渐变得规则。由以上分析可知，实际上在末敏子弹运动7 s后其扫描轨迹就达到了稳定规则，对应于图5(a)中的密集螺旋线。图5(b)为子弹完全稳定后的扫描轨迹线，为扫描间距一定的阿基米德螺旋线，其有效扫描探测范围大于200 m2，子弹稳定后的下落速度11 m/s、转速3.65 r/s以及扫描范围等结果与末敏子弹稳态扫描段的作用过程相符。

图5 不同时段下的扫描螺旋线

4 结束语

在伞弹系统旋转下落过程中，降落伞的空气阻力在短时间内与重力达到平衡，从而使其铅垂方向上的加速度降为零，此时落速达到最小值，随后一直以恒定速度下落。子弹的旋转角速度和落速变化规律基本一致，即先迅速减小后趋于稳定，在短时间内达到稳定旋转状态，转速的稳定比落速用时略多。扫描角经过大幅波动后，逐渐趋近于子弹的静态悬挂角。伞弹系统完全稳定后的扫描轨迹线为扫描间距一定的阿基米德螺旋线，其有效扫描探测范围大于200 m2。

[1] 郭锐. 导弹末敏子弹总体相关技术研究[D]. 南京: 南京理工大学, 2006.

[2] 舒敬荣. 伞弹系统三体运动分析[J]. 航空学报, 2001, 22(6): 481-485.

[3] 从明煜. 低空伞弹外弹道动力学模型[J]. 弹道学报, 2000, 12(1): 31-36.

[4] 杨绍卿. 灵巧弹药工程[M]. 北京: 国防工业出版社, 2010.

[5] 刘世平. 末敏弹四自由度质点弹道计算方法[J]. 弹道学报, 1995, 7(3): 68-74.

[6] 邱荷. 末敏弹全弹道运动仿真及虚拟现实技术研究[D]. 南京: 南京理工大学, 2013.

张 俊(1983-)，男，博士，工程师，主要研究方向为雷达天线结构设计、动力学仿真。

Dynamics Simulation of Bomb-parachute System during Falling Process Based on Adams

ZHANG Jun，CAO Jun，CHEN Min

(NanjingResearchInstituteofElectronicsTechnology,Nanjing210039,China)

The dynamic behavior of bomb-parachute system during its free falling is very complex, and simulating its characteristics of motion has a guiding significance for the structure design and stability research. Taking terminal sensitive projectile at steady state scanning stage as an example, the motion model of rotating bomb-parachute system is established, and its multi-body dynamics simulation results based on Adams software is given. Finally, the variation with flight time of various elements of ballistic trajectories is analyzed by combining the mechanism of terminal sensitive projectile and the exterior ballistics theory of projectile target. The results above can be applied to the design of bomb-parachute system and the guidance of its aerial delivery test.

bomb-parachute system; dynamics model; steady state scanning; terminal sensitive projectile

2014-10-08

TJ413+.3

A

1008-5300(2015)01-0057-04