E-凸函数的一个等价定理

王世磊，景书杰，刘争杰

（河南理工大学 数学与信息科学学院，河南 焦作 454000）

E-凸函数的一个等价定理

王世磊，景书杰，刘争杰

（河南理工大学 数学与信息科学学院，河南 焦作 454000）

E-凸函数作为凸函数的推广，近年来在凸分析、优化理论及数学规划领域中都有着重要的应用.文章首先通过定义在任意集合上函数的凸性，对E-函数的基本成分进行适当的拆分，研究得出了E-凸集与E-凸函数的相关结论；最后得出并证明了关于E-凸函数的一个等价定理，在一定程度上可丰富人们对E-凸函数的认识.

凸性；凸包；E-凸集；E-凸函数；拆分；等价定理

E-凸函数是凸函数的推广，近年来在优化理论分析中有着重要的应用，许多学者都投入到了对E-凸函数与广义E-凸函数的性质、结论及应用的研究中，并先后得到了很多重要的性质和结论[1-8].本文通过定义任意集合上函数的凸性，得到了有关E-凸函数的某些性质，最后得出了一个关于E-凸函数的新的等价定理.

对于任意一个函数，其构成不外乎定义域、值域、法则三部分，E-凸函数自然也不例外，由E-凸函数的基本定义（定义4），得到E-凸函数的定义域、值域、法则：定义域为E-凸集C；值域为R；法则为f∶C→R.下面对这三个方面进行分析：

1）定义域：本文将定义域E-凸集分拆成了3个部分，分别是C-convE（C）、E（C）、convE（C）-E（C），即：

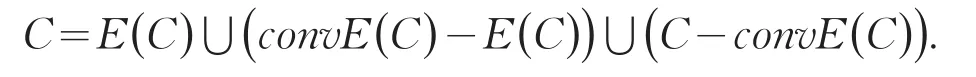
且集合E（C）、conv（C）-E（C）、C-convE（C）互不相交.集合C拆分示意图见图1.

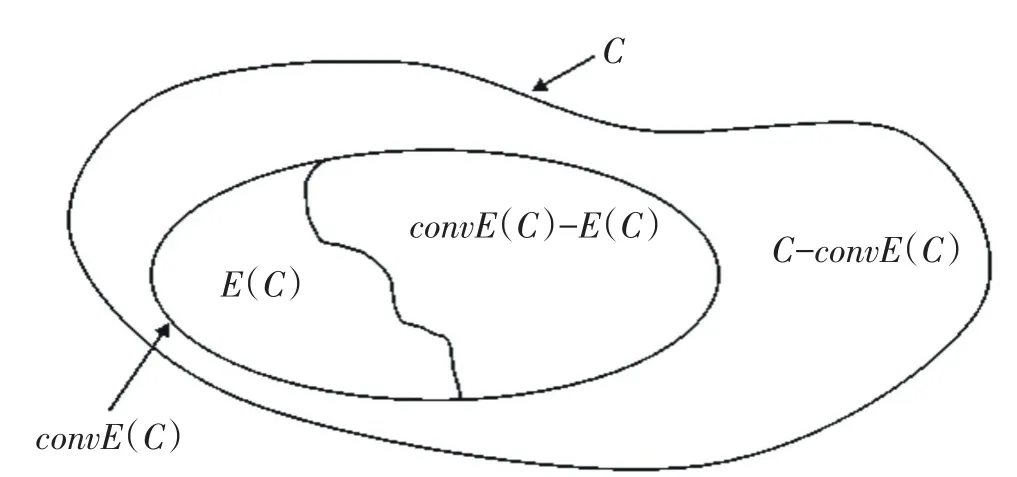
图1 集合C的拆分Fig.1 Partition of setC

为保证定义域可拆分成上面的形式，需要保证convE(C)⊂C，这将在文中给与证明（见定理1）.可以这样分拆定义域的原因是：当C是E-凸集时，E（C）并不一定是凸集，例如：

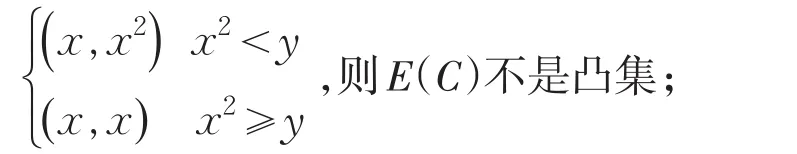
当E（C）是凸集，E（C）≠C时，可以将定义域分为两部分：convE（C）和C-convE（C）；

当E（C）是凸集时，E-凸集C即是凸集，定义域即为凸集C；

当E（C）不是凸集，convE（C）=C时，可将定义域分为两部分：E（C）和convE（C）-C.

这些都是上面分拆的特殊情况，故不加以区分.另外，之所以这样分拆定义域，其原因是convE（C）必定是凸集，而E-凸函数在凸集上具有某种特殊性质（见定理2）.

2）值域：值域取值范围为R.

3）法则：根据本文中把定义域拆分为3部分，所以将相对的法则也被分拆为3部分，记为：

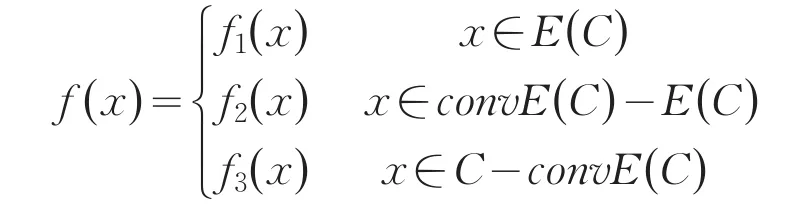
函数f拆分示意图见图2.

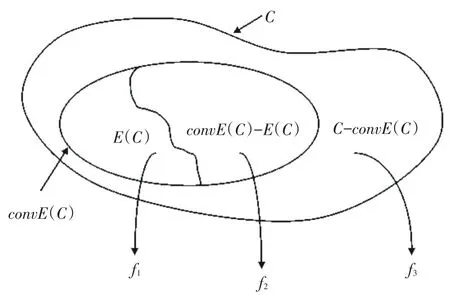
图2 函数f的拆分Fig.2 Partitiont of functionf

这样，分析E-凸函数f在E-凸集C上的性质，等价于分析f1，f2，f3在各自定义域上的性质.本文通过定义函数在任意集合上的凸性（定义6），研究E-凸函数在其定义域上的性质特征，最后得到了E-凸函数的一个等价定理（见定理3）.

1 预备知识

为了研究的需要，先引入几个与凸集、凸函数有关的基本概念.

定义1[1]称集合C⊆Rn为凸集，若对∀x,y∈C，0≤λ≤1，有：

定义2[1]称函数f∶C→R为凸函数，其中C是Rn中凸集，且对∀x,y∈C,0≤λ≤1，有：

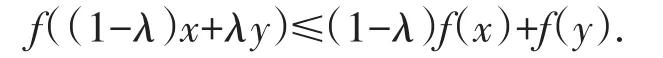
定义3[2]称集合C⊆Rn是E-凸集，若存在E∶Rn→Rn，使对 ∀x,y∈C,0≤λ≤1，有：

定义4[2]称f∶Rn→R为E-凸集C上的E-凸函数，若存在E∶Rn→Rn使得C是E-凸集，且对 ∀x,y∈C，0≤λ≤1，有：

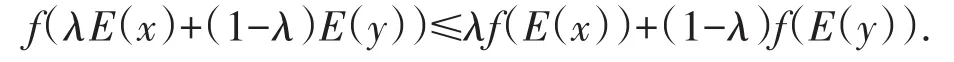
定义5[9]设S为Rn的一子集，则将包含S的所有凸集的交称为S的凸包，记为convS.

定义6[9]设f∶Rn→R是集合C上的函数，对，∀x,y∈C,0≤λ≤1若有：λx+(1 -λ)y∈C，则有f（λx+（1-λ）y）≤λf（x）+（1-λ）f（y）成立，就称函数f在集合C上具有凸性.

2 主要结论及证明

引理1[2]C是E-凸集，则E(C)⊂C.

引理2[9]设S为Rn中任一子集，则convS是由S中的元素构成的凸组合的全体.

引理3[9]C⊆Rn是E-凸集当且仅当对任何正整数m≥2，有：

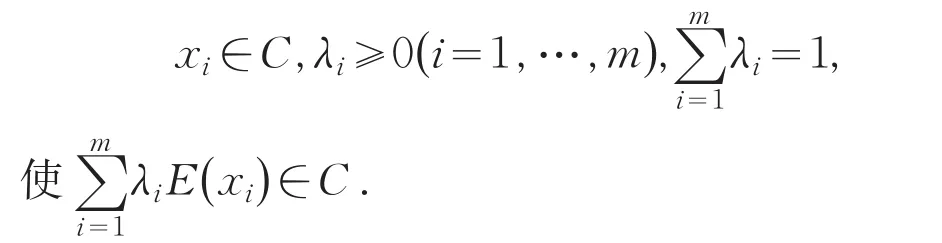
引理4[9]f∶Rn→R为E-凸集C上的E-凸函数当且仅当对任何正整数m≥2，

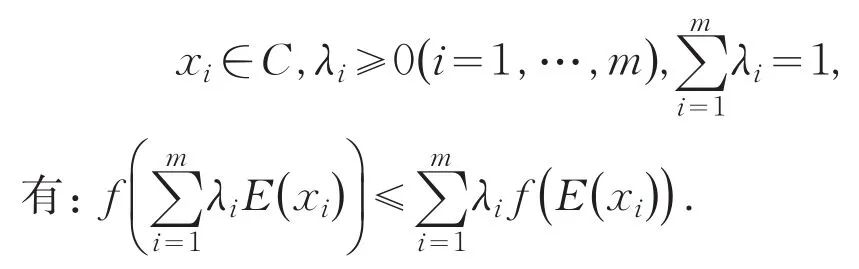
定理1C是E-凸集⇔convE(C)⊂C.

证明 ⇒)设C是E-凸集，

若E（C）是凸集，则由引理1有：

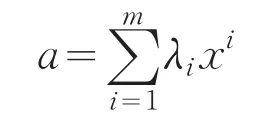
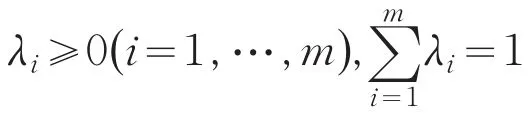
因此可得C是E-凸集.证毕.

定理2f∶Rn→R为凸集convE(C)⊂C上的凸函数，则f是E-凸集C上的E-凸函数.

证明 因为convE(C)⊂C，故由定理1知集合C是E-凸集.

又因为f∶Rn→R为凸集convE（C）上的凸函数，其中convE(C)⊂C，故对 ∀x,y∈convE(C)，0≤λ≤1有：

定理3f∶Rn→R为E-凸集C上的E-凸函数⇔

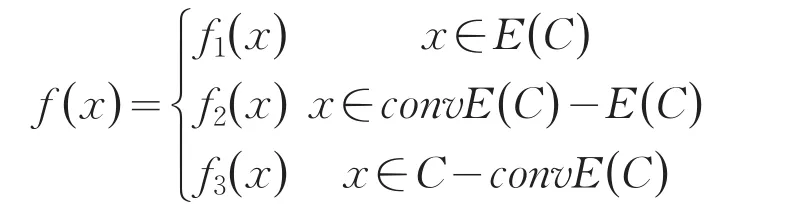
其中convE(C)⊂C，f1在E（C）上具有凸性，且maxf2≤minf1，与f3取值无关.

证明 ⇒)设f是E-凸集C上E-凸函数.

由已知C是E-凸集，故由定理1知：.

因为f∶Rn→R为E-凸集C上的E-凸函数，所以对∀x,y∈C,0≤λ≤1有：

易知上式右端最小值为minf1.又因为a是convE（C）-E（C）上任意的值，所以有：

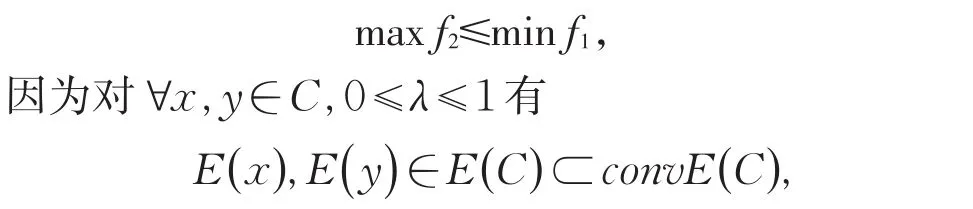
故λE（x）+（1-λ）E（y）必定属于convE（C），即（*）式左端必定与函数f3无关，换言之，函数f是E-凸集C上E-凸函数与函数f3取值无关.

⇐）若有convE(C)⊂C,则对∀x,y∈C,λ∈[0，1]，有E(x),E(y)∈convE(C).

若λE(x)+(1 -λ)E(y)∈E(C)，则由f1在E（C）具有凸性，可得：

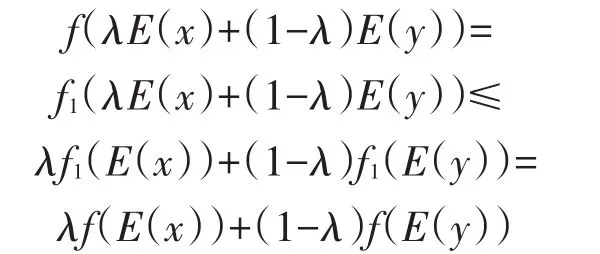
若λE(x)+(1 -λ)E(y)∈convE(C)-E(C)，由条件知 maxf2≤minf1：

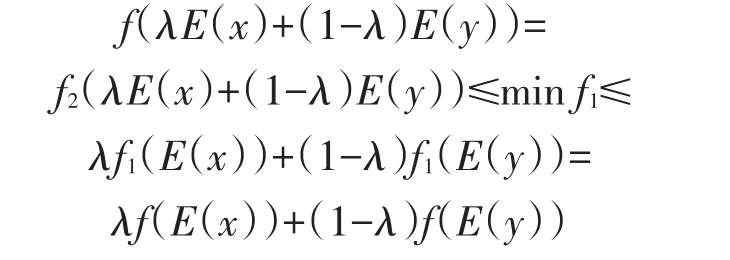
综上可知：

即：f∶Rn→R为E-凸集C上的E-凸函数.证毕.

3 结语

本文主要是从E-函数基本组成成分入手进行适当拆分，整体与局部结合进行研究，得了E-凸集、凸函数的有关结论，并最后得到了关于E-凸函数的一个新的等价定理，丰富了人们对E-凸函数的认识.但是关于E-凸函数和广义E-凸函数的性质及应用方面还有很大的研究空间，这也是今后研究工作中的重要内容.

[1]黄英全,赵克全.E-凸集,E-凸函数和半-E-凸函数[J].河北大学学报:自然科学版,2005,25(1):13-15.

[2]Youness E A.E-convex sets,E-convex functions,E-con⁃vex programming[J].Journal of Optimization Theory and Application,1999,102(2):439-450.

[3]景书杰,宋虹颖.关于广义凸的分析[D].焦作:河南理工大学,2009.

[4]宁刚.E-凸函数的若干特征[J].运筹学学报,2007,11(1):121-126.

[5]景书杰,宋虹颖.E-凸函数的一个性质[J].河南理工大学学报:自然科学版,2008,27(6):740-742.

[6]韦丽兰,黄雪燕.E-凸函数和E-拟凸函数的等价定理[J].数学的实践与认识,2011,41(15):191-197.

[7]周密.E-凸函数的一些新性质[J].海南师范大学学报:自然科学版,2012,25(1):5-8.

[8]杜君花,梁红梅.E-凸函数的若干性质[J].哈尔滨商业大学学报:自然科学版,2015,31(1):100-101.

[9]Tyrrell R Rockafellar.Convex Analysis[M].Princeton:New Jersey Princeton university,1972.

[10]胡毓达,孟志青.凸分析与非光滑分析[M].上海:上海科技出版社,2000.

[11]Dimitri P Bertsekas.Convex optimization Theory[M].北京:清华大学出版社,2011.

责任编辑：毕和平

One Equivalent Theorem ofE-convex Functions

WANG Shilei，JING Shujie，LIU Zhengjie
（School of Mathematics and Information Science，Henan Polytechnic University，Jiaozuo454000，China）

E-convex functions are the extension of convex functions and have important applications in the fields of analy⁃sis of convexity,optimization theory and mathematical programming in recent years.Firstly,by defining the convexity of func⁃tion in any set and properly partitioning the basic compositions ofE-convex functions,we gave some new conclusions ofE-convex sets andE-convex functions.Finally,we gained and proved one equivalent theorem ofE-convex functions.All of these can,to a certain extent,enrich people's knowledge ofE-convex function.

convexity；convex hull；E-convex set；E-convex function；partition;equivalent theorem

O 174.13

A

1674-4942(2015)02-0127-04

2015-03-02

河南省一级重点学科（数学）支持项目；河南理工大学校级重点学科（运筹学与控制论）支持项目