求解BTTB系统的迭代算法

曹蓉

（汕头职业技术学院 自然科学系，广东 汕头 515041）

求解BTTB系统的迭代算法

曹蓉

（汕头职业技术学院 自然科学系，广东 汕头 515041）

BTTB矩阵在信号处理等工程问题中有着广泛的应用，因此，针对这种类型矩阵的特点，利用它们的结构来设计一些数值稳定的、收敛性能好的快速算法，具有极为重要的意义.文章讨论了块三角Toeplitz矩阵的一些性质，给出了求解块下三角Toeplitz矩阵逆的快速算法，并对其复杂性进行了分析.利用这种求逆算法进而给出了求解BTTB系统的块Gauss-Seidel迭代算法和块SOR迭代算法，并讨论了其收敛性.数值实验得到验证.

BTTB；块Gauss-Seidel迭代；块SOR迭代

Toeplitz矩阵出现在数字信号处理领域的许多应用中，是应用最广泛的特殊矩阵之一.这些问题很多都归结为对Toeplitz系统的求解.因此涌现了很多关于Toeplitz系统的快速求解，如[1-5].特殊的BTTB矩阵在高维信号、图像复原、数值偏微分方程、折积型积分方程等有广泛的应用.因此，针对这类型矩阵的特点，利用它们的结构来设计一些数值稳定的、收敛性能好的快速算法具有极为重要的意义.现在已有一些人对块Toeplitz系统和特殊的BTTB系统求其快速算法[6-9].因此本文在此基础上利用B-FFT技术，讨论BTTB系统的求解.对于这些线性方程组的求解主要分为直接法和迭代法.由于直接法求解的运算量为O（N3），另外直接解法非常不稳定，因此更多人选择迭代法求解.对于迭代法，一个好的预条件子能使其运算量大大降低，因此人们更专注于迭代法的研究.M.K.Ng在1997年给出了mn阶BTTB方程组的带状预处理迭代法[10].H.Akaike和游兆永[11-12]已对块Toeplitz矩阵求其逆给出算法.本文利用B-FFT技术给出块三角BTTB矩阵的快速求逆算法，并将这个求逆算法应用到块Gauss-Seidel迭代算法和块SOR迭代算法.

一个矩阵Am，n有如下结构

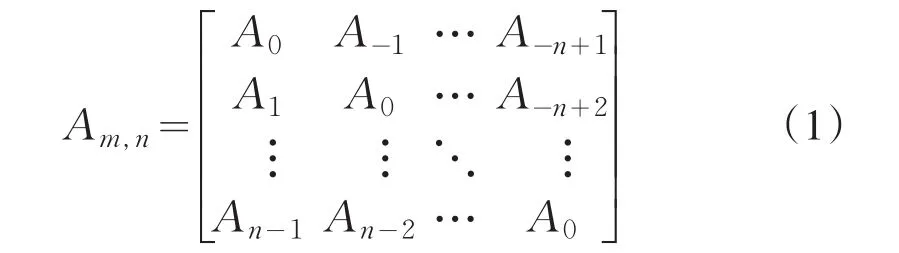
则称Am，n为一个m，n阶的块Toeplitz矩阵，其中Ai（1-n≤i≤n-1）为m阶的任意矩阵，即Am，n主对角线上的分块矩阵相同，且平行于主对角线线上的分块矩阵也相同.若Ai（1-n≤i≤n-1）为Toeplitz矩阵，即则称Am，n为 BTTB（Block-Toeplitz-Toeplitz-Block）矩阵.

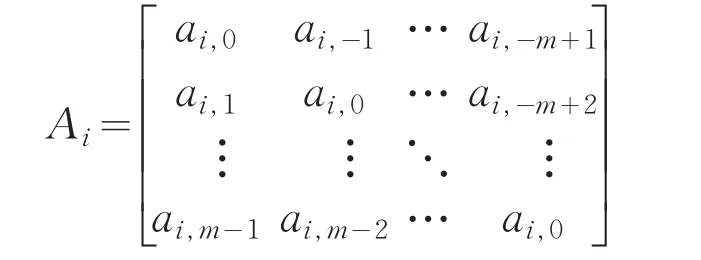
对于求解线性方程组Am，nx=b（Am，n为（1）中的形式）的迭代格式一般可表示为

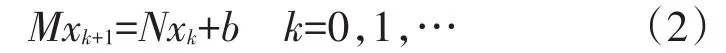
其中Am，n=M-N为矩阵Am，n的分裂.如果M非奇异，显然，任给初始向量x0，由方程（2）生成的迭代序列{xk}收敛的充要条件是迭代矩阵H=M-1N的谱半径ρ（H）＜1.下面首先讨论块下三角BTTB矩阵的逆.

1 块下三角BTTB矩阵的逆

定义1[13]如果Am，n=（Ai）是一个mn阶的Toeplitz矩阵，则Am，n=C（1∶mn，1∶mn），其中C是一个（2n-1）m阶的块循环矩阵且：

定理1[13]一个块Toeplitz矩阵乘一个块向量可转化为一个块循环矩阵乘这个块向量.

即若Y=CX，C为（3）中的块循环矩阵，X，Y分别为mn维的块向量，X（i），Y（i）表示块向量X，Y的第i个m维向量，并且X=（n+1∶2n-1）=0，0为（n-1）m维的零向量，则.

推论1[13]块循环矩阵Cm，n可块对角化，即：

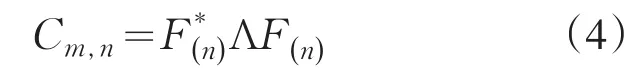
其中F(n)=Fn⊗Im，Fn是n阶离散Fourier变换（Dis⁃crete Fourier Transform即DFT）矩阵，满足⊗表示Kronecker积，Λ表示一个mn阶的对角阵，即Λ=Blkdiag（F（n）Cm，n（∶，1∶m）），这里Cm，n（∶，1∶m）是块矩阵Cm，n的前m列（即第1列块），Blkdiag是由括号里的块向量生成的块对角阵.由参考文献[14]知，若vec(Y)=(Fn⊗Im)vec(X)，则能得到

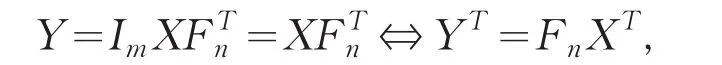
因此形如z=Cm，nx的这种一个块循环矩阵与一个向量相乘可以使用B-FFT技术，由公式（4）知，

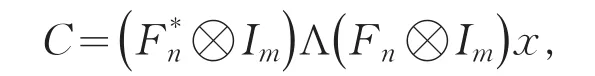
引理1[1]表示阶数为mn阶的块下三角To⁃eplitz矩阵的集合：

由此可得出，A-1的递归方程：

根据引理1、推论1和推论2得到块下三角BTTB矩阵逆的快速算法.从推论2中公式（6）知，若计算块下三角BTTB矩阵AM的逆，当知道了时，则，只需要计算BN.由引理1的（c）知，是一个块下三角Toeplitz矩阵，因此，只需求出BN的第1列块，它的第1列块等于积的第1列块，而与CN都是块Toeplitz矩阵，能嵌入到块循环矩阵.另外注意到，BTTB矩阵Am，n的每一小块也是To⁃eplitz矩阵.

下面给出块下三角BTTB矩阵的逆的算法.不妨设n=2q，min=2l，（0≤l＜q）.对于n非2的幂，见后面的分析.

算法1 块下三角BTTB矩阵的逆的快速算法.

算法1中的函数hti（·）指的是Doubling算法[15]，cirsys（·）指的是利用FFT技术计算循环矩阵乘以一个向量，strass（·）表示两个矩阵相乘的Strassen算法，blkcirsys（·）与bttbcirsys（·）均利用B-FFT技术计算块循环矩阵乘以块向量.

当n非2的幂时（如2q-1＜n＜2q），计算块下三角BTTB矩阵Am，N（N=2q）的逆，它的第1列块是Am，n的第1列块和m阶的零块矩阵，即（A0，A1，…，An-1，O，…，O）.引理1的（d）保证了Am，N的第1列块的前n个与Am，n的第1列块相同.

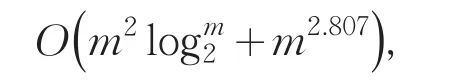
因此这三个算法的复杂度近似为

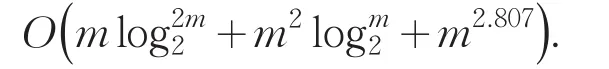
先讨论块循环矩阵乘以块向量的复杂度.由推论1知，计算y=Cm，nx，x=（x1，x2，…，xn）T，xi是个m维向量，可以使用B-FFT计算，即

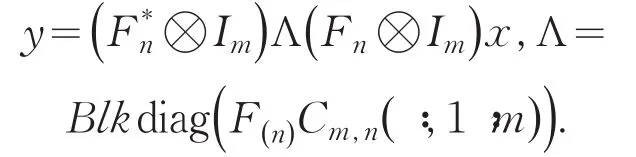
因此一个mn阶的块循环矩阵乘以块向量使用B-FFT和基2-FFT后的复杂度为

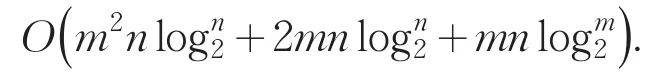
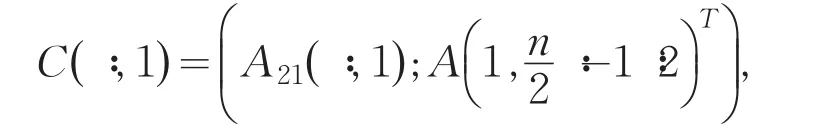
此时的矩阵大小为（n-1）m×（n-1）m，因此计算的第1列块的复杂度为

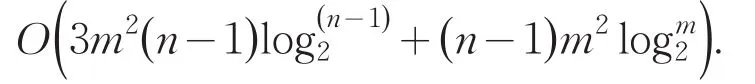
2 BTTB矩阵的两种迭代算法

a）块Gauss-Seidel迭代算法

给定方程组Am，nx=b（Am，n为（1）中的形式），令Am，n=D-L-U，其中

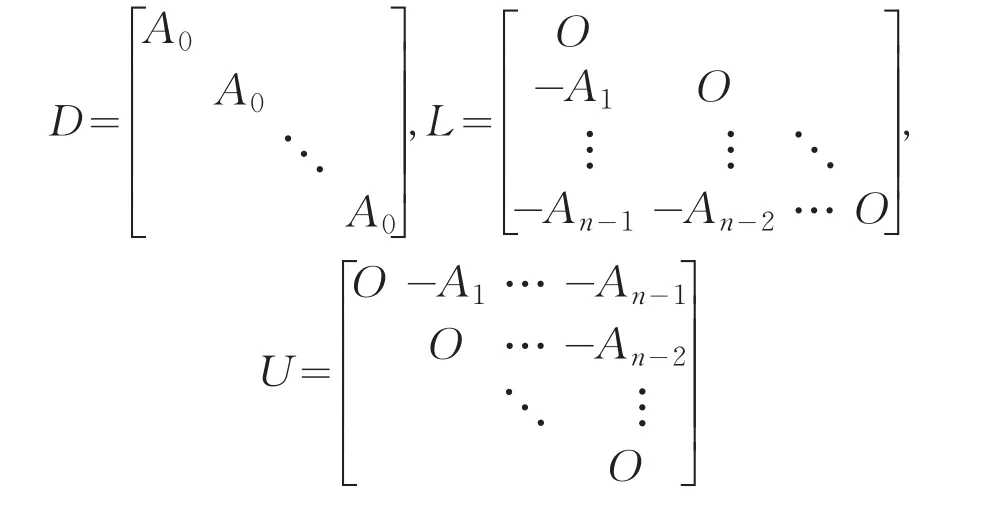
如果在方程组（2）中取，M=D-L，N=U那么就得到如下求解Am，nx=b的块Gauss-Seidel迭代格式：

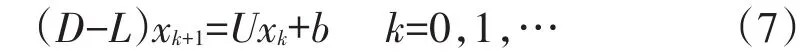
可以看到D-L是块下三角BTTB矩阵，故可以利用算法1求其逆，因此得到块Gauss-Seidel算法如下：

算法2 块Gauss-Seidel迭代算法

1）给定Am，n，x0，b，n=0，精度e；

2）利用算法1求D-L逆H；

3）使用B-FFT计算H*b；

4）Fork=1，2，…

5）使用基2-FFT和两次B-FFT计算HUxk；

6）xk+1=HUxk+Hb n=n+1；

7）当‖xk+1-xk‖2＜e时，停止；

8）输出xk+1，n.

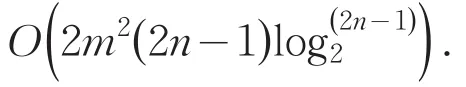
b）块SOR迭代算法

将线性方程组Am，nx=b两边两边乘以ω变为ωAm，nx=ωb，且在ωAm，n=M-N中取M=D-ωL，N=[ωU+（1-ω）D]，那么得到如下求解ωAm，nx=ωb的块SOR的迭代格式

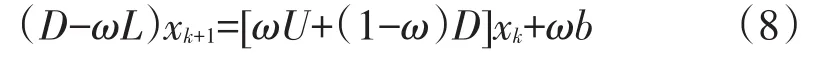
其中（0＜ω＜2），由于D-ωL是块下三角BTTB矩阵，所以可以由算法1求得其逆.由此给出块SOR迭代算法如下：

算法3 块SOR迭代算法

1）给定Am，n，x0，b，n=0，精度e；

2）利用算法1求D-ωL逆H；

3）使用B-FFT计算H*b；

4）Fork=1，2，…

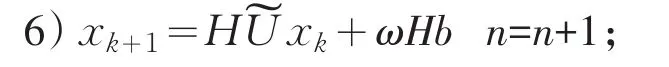
7）当‖xk+1-xk‖2＜e时，停止；

8）输出xk+1，n.

3 迭代法的收敛性

定义2[16]一个矩阵A=(aij) ∈Rn×n，称为：

（1）非负矩阵，如果aij≥0，i，j=1，2，…，n；

（2）Z型矩阵，如果aij≤0，i≠j，i，j=1，2，…，n；

（3）M矩阵，如果A是非奇异的Z矩阵且A-1≥0；

（4）H矩阵，如果其比较矩阵〈A〉是非奇异的且它是M矩阵，这里〈A〉=（αij），其中

定义3[17]若A,B∈Rm×n且满足A-B≤O，则称A小于等于B，记为A≤B.

定义4[17]若A=(aij)∈Rm×n，则定义A的绝对值为每个元素的绝对值，记为|A|=(|αij|).

注意：不能与“方阵的行列式”混淆.

定义2 一个n阶矩阵A的分裂A=M-N称为：

（1）弱正则分裂，如果M-1≥0，且M-1N≥0；

（2）P-正则分裂，如果MT+N正定.

引理2 如果A=(aij)∈Rn×n对称正定，且A=M-N，P-正则分裂，则ρ（M-1N）＜1；如果A为M矩阵，且A=M-N，弱正则分裂，则ρ（M-1N）＜1.

引理3 令A,B∈Rn×n，

（1）若A是一个M-矩阵，B∈Zn×n（全体n阶Z型矩阵构成的集合），且A≤B，则B也是一个M-矩阵；

（2）若A是一个H-矩阵，则；

（3）若|A|≤B，则ρ（A）≤ρ（B），ρ（A）表示A的谱半径.

定理2 如果（1）式中Am，n为H-矩阵或对称正定，则对任给初始向量x0，则方程（7）生成的迭代序列{xk}收敛.

证明 根据引理2只要验证块Gauss-Seidel分裂满足收敛性的条件即可.

当Am，n为对称正定时，D也对称正定.又（D-L）T+U=D，即Am，n=（D-L）-U为P-正则分裂，故满足收敛条件.

当Am，n为H-矩阵时，〈Am，n〉为M-矩阵.由引理 3（1）知，〈D-L〉为M矩阵，|U|为非负矩阵，于是有〈D-L〉-1≥0，.即〈Am，n〉=〈D-L〉-|U|为弱正则分裂，于是

又ρ(B)≤ρ(|B|)和ρ（B）≤ρ（C），如果C≥B≥0以及矩阵不等式有

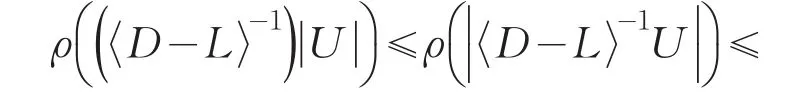
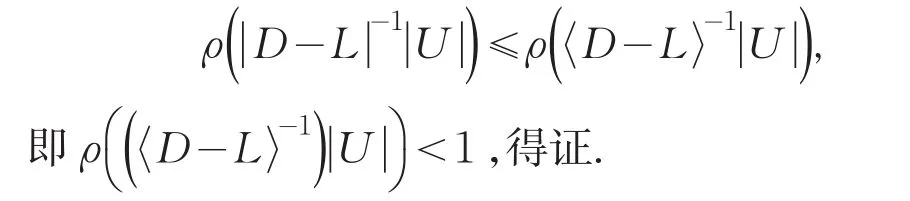
定理3 如果式（1）中Am，n为H-矩阵或对称正定，则任给初始向量x0，由方程（8）生成的迭代序列{xk}收敛.

证明 根据引理2只要验证块SOR分裂满足收敛性的条件就行.

当Am，n为对称正定时，又0＜ω＜2，所以（2-ω）Am，n对称正定，容易知道块对角矩阵（2-ω）D也对称正定.又

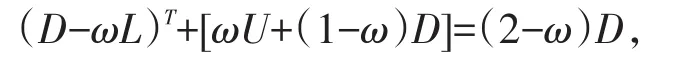
即ωAm，n=（D-ωL）-[ωU+（1-ω）D]为P-正则分裂，故满足收敛条件.

当Am，n为H-矩阵时，ωAm，n也为H-矩阵，〈ωAm，n〉为M-矩阵，〈D-ωL〉为M-矩阵，|ωU+(1 -ω)D|为非负矩阵，

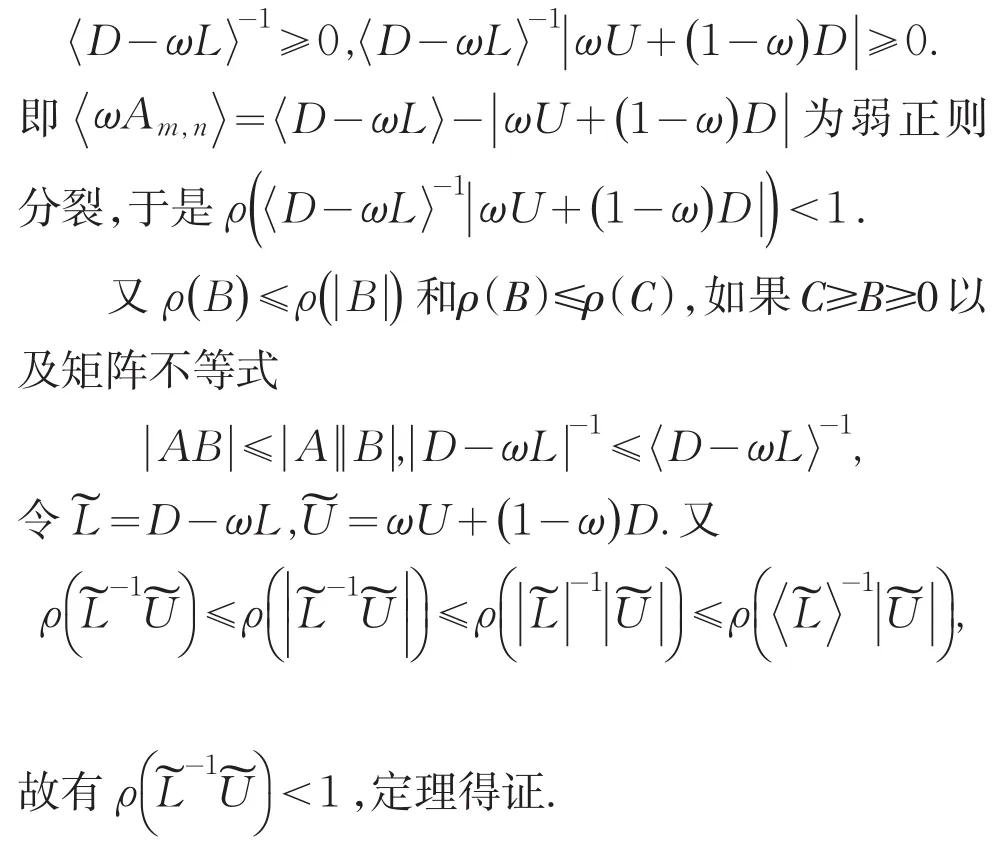
4 结论

本文主要利用B-FFT给出块下三角BTTB矩阵快速求逆算法，利用其算法给出BTTB系统的两种迭代算法，分析其收敛性.不足之处，由于BTTB矩阵本身的特殊性，是否可将其收敛的条件进行改进！

[1]徐仲,张凯院,陆全.Toeplitz矩阵类的快速算法[M].西安:西安工业大学出版社,1999:38-45.

[2]曹蓉,童细心.求解Toeplitz系统循环和反循环分裂算法[J].云南民族大学学报:自然科学版,2012,21（5）:356-360.

[3]Ng M K.Iterative Methods for Toeplitz Systems[M].Ox⁃ford:Oxford University Press,2004.

[4]Chan R H,Ng M K.Conjugate gradient methods for To⁃eplitz systems[J].SIAM Rev,1996,38(3):427-482.

[5]毕永青.三对角对称Toeplitz矩阵的解析逆阵[J].西南民族大学学报:自然科学版,2003,29（4）:390-393.

[6]Shi Yongjie,Pi Xuebo.New preconditioners for systems of linear equations with Toeplitz structure[J].Calcolo,2014,51(1):31-55.

[7]Lin furong,Wang chixi.BTTB preconditioners for BTTB systems[J].Numerical Algorithms,2012,60(1):153-167.

[8]冯月华,刘成志,刘仲云.块Toeplitz方程组的快速块Gauss-Seidel迭代算法[J].数学理论与应用,2012,32(1):1-5.

[9]赵敏.块Toeplitz矩阵的一种快速QR分解及算法实现[J].长江大学学报:自然科学版,2007,4(2):4-5.

[10]Ng M K.Band precondtioners for Block-Toeplitz-To⁃eplitz-Block Systems[J].Linear algebra and its applications,1997,259:307-327.

[11]Akaike H.Block Toeplitz matrix inversion[M].SIAM J.Ap⁃pl.Math,1973,2(4):234-241.

[12]游兆永,路浩.块Toeplitz三角阵求逆及块Toeplitz三角线性方程组求解的复杂性[J].数学研究与评论,1989,9（1）:101-106.

[13]金小庆.Toeplitz系统预处理方法[M].北京:高等教育出版社,2010:59-72.

[14]张凯院,徐仲.数值代数[M].2版.北京:科学出版社,2006:36-45.

[15]Morf M.Doubling algorithms for Toeplitz and related equa⁃tions[J].In:IEEE Conference on Acoustics Speech and Sig⁃nal Processing,1980:954-959.

[16]Commges D,Monsion M.Fast Inversion of Triangular To⁃eplitz Matrices[J].IEEE Transactions on automatic control,1984,29(3):250-251.

[17]方保镕,周继东,李医民.矩阵论[M].北京:清华大学出版社,2004:330-354.

责任编辑：毕和平

The Iterative Algorithm for Block-Toeplitz-Toeplitz-Block Systems

CAO Rong
（Natural Sciences，Shantou Vocational and Technical College，Shantou515041，China）

BTTB matrices have a wide range of engineering applications such as in signal processing.In view of the charac⁃teristics of this type of matrix,it is very significant that we design some fast algorithms with numerical stability and the good property of convergence.Firstly,we discussed some properties of block triangular Toeplitz matrices,then we presented fast algorithms for computing the inverse of such a class of matrices and also analyzed the complexity of this algorithm.Using the inverse algorithm,we gave Block-Gauss-Seidel iteration algorithm and Block-SOR iteration algorithm for solving the BTTB system.

BTTB；Block Gauss-Seidel iteration；Block SOR iteration

O 241.6

A

1674-4942(2015)02-0134-05

2015-03-01

汕头职业技术学院科研基金资助项目（SZK2014Y35）