对数线性Gamma分布模型极大似然估计的强相合性和渐近正态性

刘双花，尹长明，邓娌莉

（1.百色学院 数学与计算机信息工程系，广西 百色 533000；2.广西大学 数学与信息科学学院，广西 南宁 530004）

对数线性Gamma分布模型极大似然估计的强相合性和渐近正态性

刘双花1，尹长明2，邓娌莉1

（1.百色学院 数学与计算机信息工程系，广西 百色 533000；2.广西大学 数学与信息科学学院，广西 南宁 530004）

在‖Zn‖=o(logn)和（对某个c＞0，α＞0）等条件下，证明了对数线性Gamma分布模型极大似然估计（MLE）的强相合性和渐近正态性，其中设计阵序列{‖Zn‖}可以为无界序列.

对数线性Gamma分布模型；强相合性；渐近正态性

1 引言和主要结果

广义线性模型（GLM）是一般线性模型的重要推广，它既适用于连续数据，又适用于离散数据，特别是后者.自从Nelder和Wedderburm[1]引入此模型以来，就得到了广泛地应用，尤其是在生物、医学和社会数据的统计分析等领域．

假设响应变量yi服从Gamma分布，且密度函数为

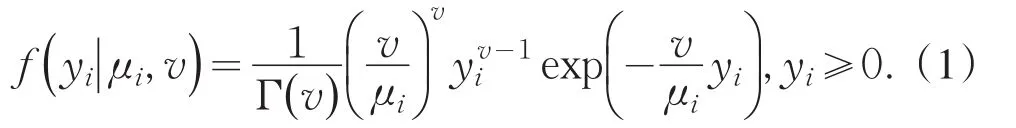
这里，yi是响应变量，μi是期望且μi＞0，v是形状参数且v＞0．

当联系函数取自然联系函数时，就得到了线性Gamma分布模型，有

由于均值μi＞0，那么线性预测，这样对β就增加了限制.而当联系函数取

时，就得到对数线性Gamma分布模型，不需要对β加以限制．

根据（1），可知yi的对数似然函数为

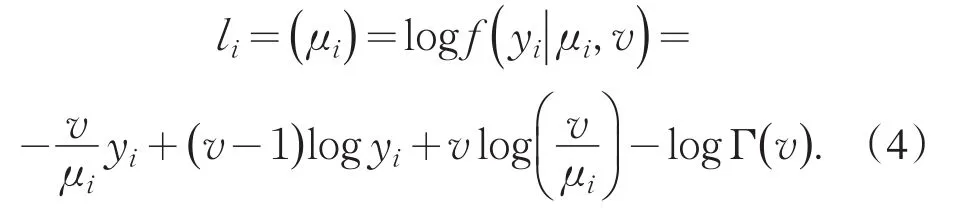
根据（3）和（4）有

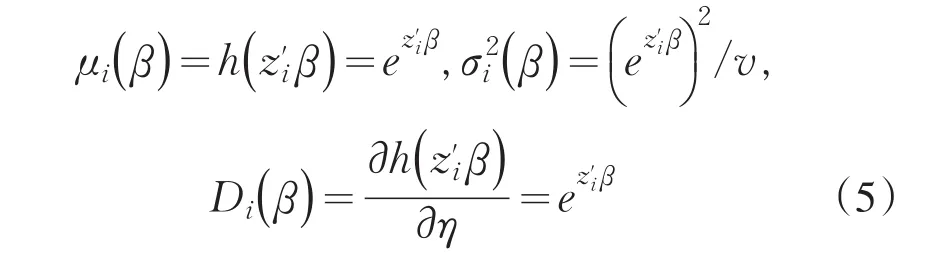
可知得分矩阵和信息矩阵分别为

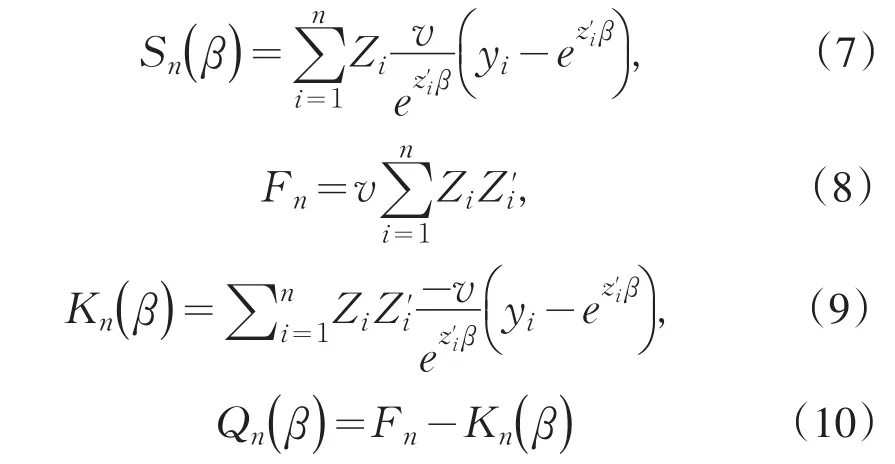
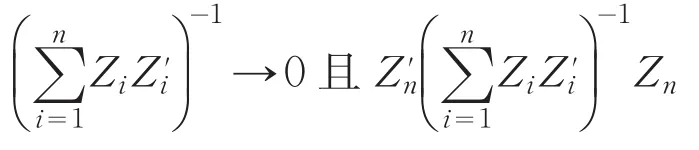
等来证明了GLM极大似然估计的相合性和渐近正态性.在非自然联系情况下，由条件

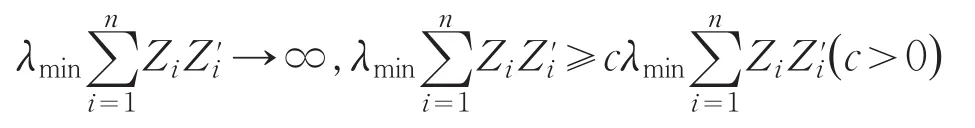
等证明了GLM极大似然估计的相合性和渐近正态性，这里Fn表示信息矩阵Fn（β）在β0处的取值，

是标准化的信息矩阵，λmaxA（λminA）表示矩阵A的最大（小）特征根.本文去掉{Zi，i≥1}有界的限制，在‖Zn‖=o(logn) 和（对某个c＞0，α＞0）等条件下，建立了对数Gamma分布模型MLE的强相合性和渐近正态性，即下面定理．

定理1 假设β0是对数线性Gamma分布模型回归参数向量β的真值且满足下列条件：

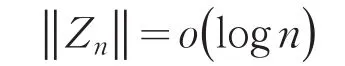
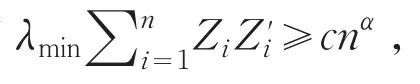
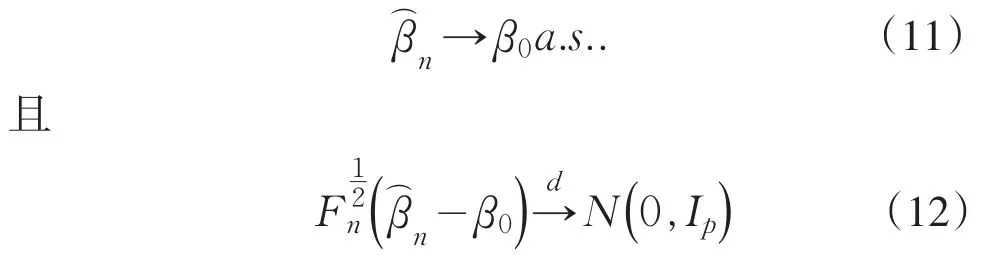
2 定理的证明

为了定理的证明，先引入下列引理：

引理1[10]（Bernstein不等式）设x1，x2，…，xn是独立的随机变量，|xi|≤b＜∞,Exi=0,i=1,2,…,n.记则对任意ε＞0

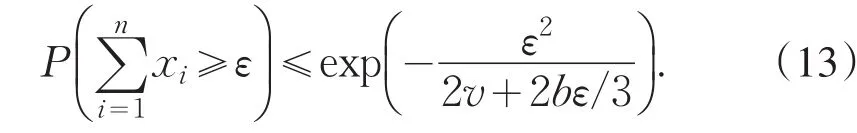
引理2[11]（向量值函数中值定理）设X=（x1，x2，…，xp）′，F=（f1，f2，…，fp）′.

如果fi=fi（x1，x2，…，xp）（i=1，2，…，p）在凸集上G⊂kp上连续可微，则对任意α,β∈G，有

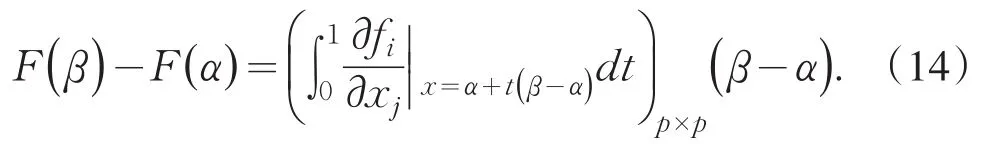
因为由定理1的条件知，‖Zn‖=o(l ogn)，其中β在β0的附近，则对充分小的，有i-ε≤eZiβ≤iε[36].

为证（15）式，只需证明以概率1，当n充分大时，

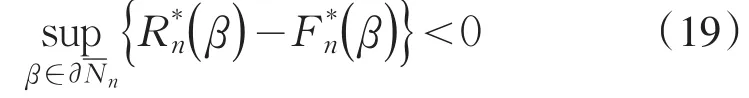
取足够大的某个s，记r=2s+1，

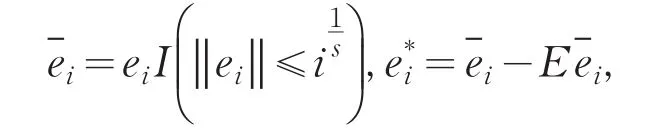
其中I（·）是示性函数.再根据Cr不等式有

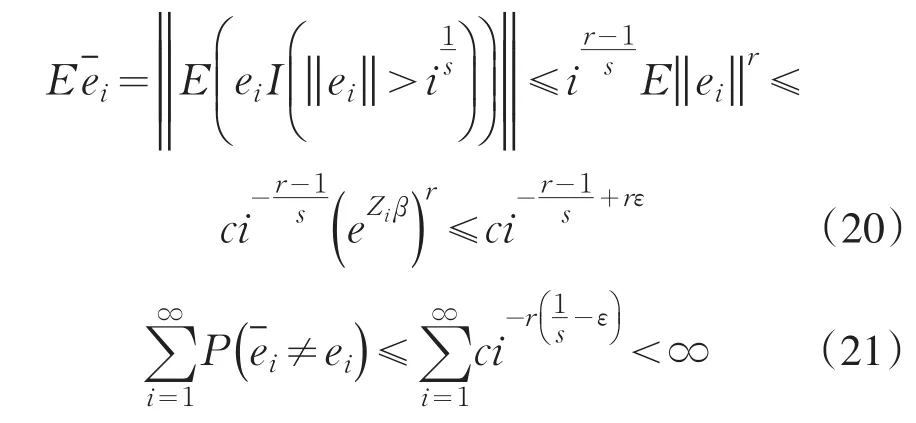
所以由Borel-Cantelli引理知，以概率1，当n充分大时，

由定理1的条件知，

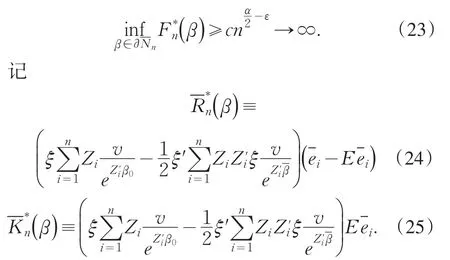
根据（22），（23），（24）和（25）式知，为证（19）式，等价于证明以概率1，当n充分大时，

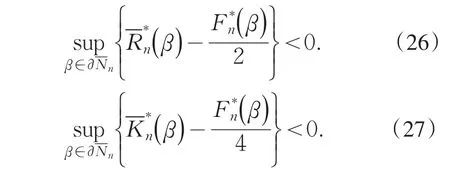
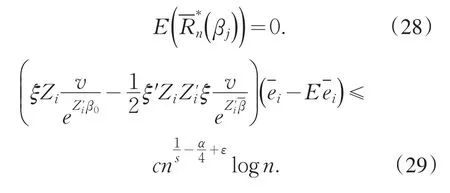
根据引理1，（29），和（30）知

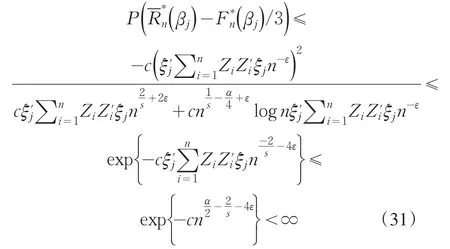
由Borel-Cantelli引理，以概率1，当n充分大时，

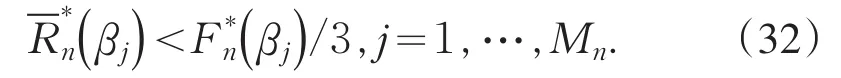
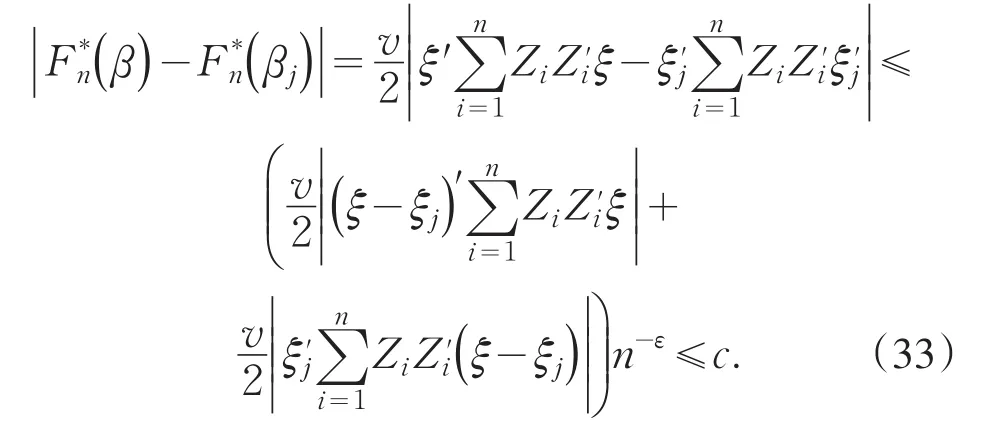
同理可证，由中值定理

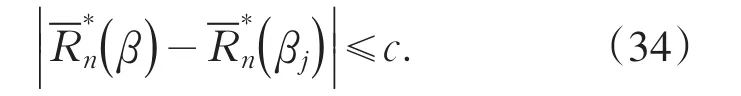
由（23）、（32）、（33）和（34）式，以概率1，当n充分大时，（26）式成立．

故由（23）和（35）式，以概率，当n充分大时，

因此（27）式成立.由（26）和（27）知，以概率，当n充分大时，（19）和（15）式成立.从而存在使得（11）和下面的（37）式成立．

下面证渐近正态性．

根据（37）式和引理2得

由Linderberg中心极限定理知（40）成立.

其次证明，当n→∞时，有

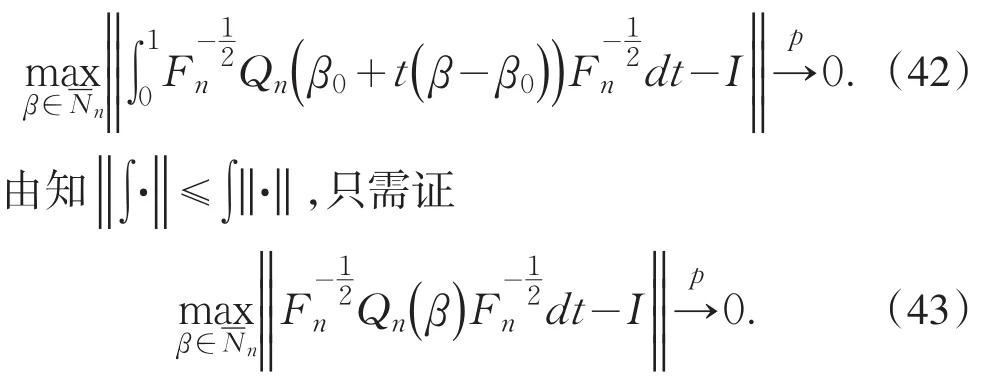
根据（7）（8）（9）和（10）式可得

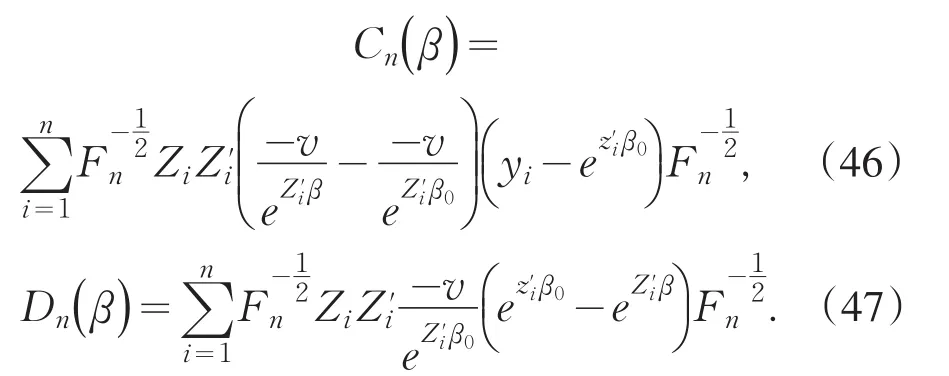
由定理1的条件知，

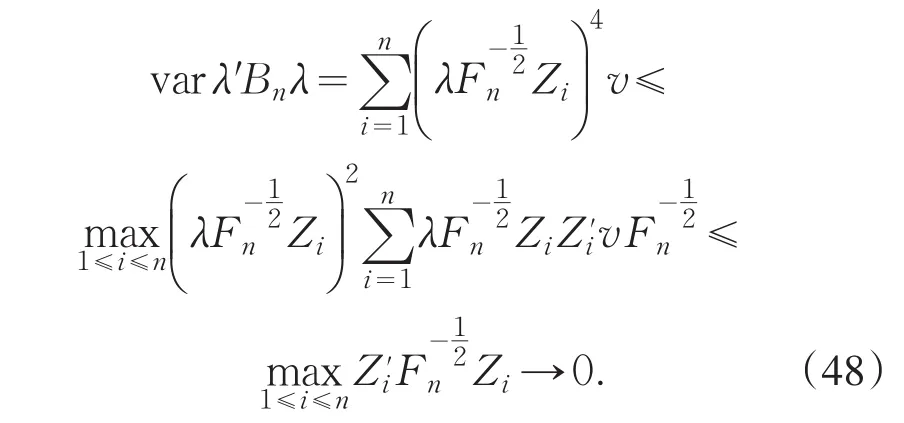
根据Markov不等式知

由（52），（51），（49）和（44）知（43），（42）成立.

最后，根据（37）、（40）和（42）可得，（12）成立．

[1]Nelder J A,Wedderburm R W M.Generalized linear models[J].J Roy Statist Soc Ser A,1972,135:370-384.

[2]Fahrmeir L,Kanfmann H.Consistency and asymptotic nor⁃mality of the maximum likelihood estimator in generalized linear models[J].Ann.Statist,1985,13:342-368.

[3]Yue L,Chen X R.Rates of a.s.convergence of the maxi⁃mum quasi-likelihood estimator in generalized linear models[J].Science in China,Ser A.(in Chinese),2004,34:203-214.

[4]Yin C H,Zhao L C,Wei C D.Asympotic normality andstrong consistency of maximum quasi-likelihood estimates in generalized linear models[J].Science in China,Ser A 2006,48:145-157.

[5]Chen K,Hu I,Ying Z.Strong consistency of maximum qua⁃si-likelihood estimation in generalized linear models with fixed and adaptive designs[J].Ann Statist,1999,27:1155-1163.

[6]Gao Q B,Lin J G,Zhu C H,et al.Asymptotic properties of maximum quasi-likelihood estimators in generalized linear models with adaptive designs[J].Statistics,2012,46:833-846.

[7]Zhang S G,Liao Y.On some problems of weak consistency of quasi-likelihood estimates in generalized linear models[J].Sci China Ser A,2008,51:1287-1296.

[8]Ludwing Fahrmeir,Gerhard Tutz.Multivariate Statistical Modeling Based on Generalized Linear Models[M].New York:Spring-Verlag,1998:15-304.

[9]邓娌莉,尹长明,刘双花.对数线性Gamma分布模型极大似然估计的渐近正态性[J].广西师范学院学报:自然科学版,2013,30(1):32-35.

[10]Bennett G.Probability inequality for sums of independent random variables[J].J Amer Statist Assoc,1962,57:33-35.

[11]陈希孺.广义线性模型的拟似然法[M].合肥:中国科学技术大学出版社,2011:2-4.

责任编辑：毕和平

Strong Consistency and Asymptotic Normality of the Maximum Likelihood Estimator in the Log Linear Gamma Model

LIU Shuanghua1，YIN Changming2，DENG Lili1
（1.Depatment of Mathematics and Computer Information Engineering，Baise University，Baisei533000，China；2.Mathematics and Information Science，Guangxi University，Nanning530004，China）

In the log linear Gamma model,under assumptions that ‖Zn‖=o(logn)andfor somec＞0,α＞0,the strong consistency and asymptotic normality of the maximum likelihood estimates of the regression parameter vector were established,whereZnare regressors.

the log linear Gamma model；strong consistency；asymptotic normality

O 212.1

A

1674-4942(2015)02-0122-05

2015-03-08

百色学院一般科研项目（2014KB09）