基于集对分析的多值信息系统粗糙集模型

李长清，张燕兰

（1.闽南师范大学 数学与统计学院，福建 漳州 363000；2.闽南师范大学 计算机学院，福建 漳州 363000）

基于集对分析的多值信息系统粗糙集模型

李长清1，张燕兰2

（1.闽南师范大学 数学与统计学院，福建 漳州 363000；2.闽南师范大学 计算机学院，福建 漳州 363000）

鉴于多值信息系统下相似关系和容差关系存在的局限性，结合集对分析思想，给出一种集对联系度粗糙集模型,这种模型比以上两种模型更广.

多值信息系统；相似关系；容差关系；集对分析；联系度相似关系

经典粗糙集理论[1]是波兰数学家Pawlak Z.于1982年提出的，它是一种处理不确定和不完整问题的新型数学工具，现已在决策与分析、数据挖掘、机器学习、模式识别、智能信息处理[2-6]等诸多领域得到广泛应用.经典粗糙集处理的是完备信息系统，而在现实应用中，由于对数据获取的限制，系统属性值大都存在不唯一，系统成了多值信息系统.对多值信息系统的处理已有很多模型[7-9]，相似关系[4]和容差关系[10]是两种最普遍的模型，但这两种模型都存在局限性.

集对分析方法[11]是赵克勤教授提出的用于研究集合之间不确定性关系的一种新理论，现已得到广泛的应用[12-16].本文针对相似关系和容差关系两种模型存在的局限性，结合集对分析的思想，提出一种集对粗糙集模型，克服了这两种模型的局限性，并证明集对粗糙集模型是这两种模型的推广.

1 联系度相似关系

定义1[4]设S=〈U，A∪{d}〉为一个信息系统，其中U是论域，A是条件属性集，{d}是决策属性集.∀a∈A⋃{d}，有a∶U→Va，其中Va为a的值域.若对于∀u∈U,a∈A，有|a(u)|=1，则称S是完备信息系统；否则称S是多值信息系统（或不完备信息系统），|∙|表示集合的基数.

定义2[4]设S为多值信息系统，∅≠B⊆A,B上的相似关系定义为：

SIMB满足自反性和对称性，但不满足传递性.u在B上的相似类为：

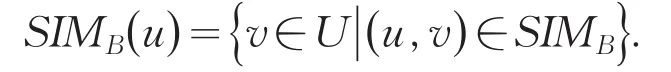
定义3[4]设S为多值信息系统，∅≠B⊆A，若|b(x)|＞1，则令b（x）=*（*表示空值），B上的容差关系定义为：

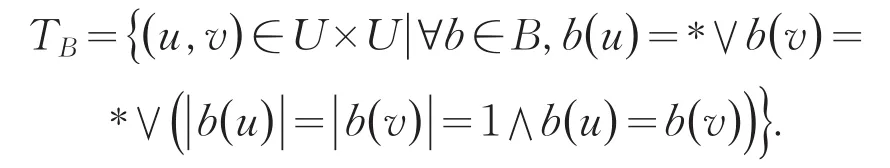
TB满足自反性和对称性，但不满足传递性.u在B上的容差类为：TB(u)={v∈U|(u,v)∈TB}.

相似关系和容差关系都是对经典不可分辨关系的拓展，但这两种模型都存在局限性.例如对u1=（1，2，3，…，50），u2=（0，2，3，…，50），相似关系认为u1与u2完全不同，必须划在不同类中，这会使划分过细，特别不适合对大型多值信息系统的处理.而例如对v1=（1，{1，3}，3），v1=（{2，3}，2，{1，2}），可令v1=（1，*，3），v1=（*，2，*），容差关系认为v1与v2不可分辨，必须划在同一类中，而事实上，v1与v2完全不可能相同.因此，这两种关系在多值信息系统下都存在局限性.

定义4[14]设S为多值信息系统∅≠B⊆A,∀u,v∈U，u和v在B下的集对联系度：

这里p=|M(u,v)|/n表示u和v在B下的同一度，q=|M(u,v)|/n表示u和v在B下的差异度，r=|K(u,v)|/n表示u和v在B下的对立度，n=|B|.

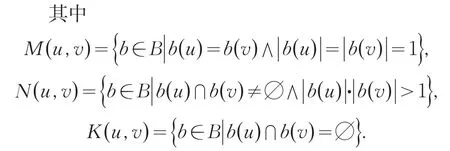
定义5 设S为多值信息系统，∅≠B⊆A，0≤α，β≤1，联系度相似关系定义为：

PB满足自反性和对称性，但不满足传递性.u在B上的联系度相似为：PB(u)={v∈U|(u,v)∈PB}.

定理1 设S为多值信息系统，∅≠B⊆A，PB是联系度相似关系，SIMB是相似关系，则当α=β=0时，PB=SIMB.

定理2 设S为多值信息系统，∅≠B⊆A，PB是联系度相似关系，TB是容差关系，则当α=0，β=1，时，TB⊆PB.

此定理显然成立.

由定理1与2可以看出联系度相似关系是相似关系和容差关系的推广.

2 上、下近似和变精度

定义6 设S为多值信息系统，∅≠B⊆A,∀X⊆U,X在联系度相似关系下的上、下近似分别为：

性质1 设S为多值信息系统，∅≠B⊆A，∀X,Y⊆U，容易验证以下性质：

上、下近似考虑的是元素u所在类包含于X的情况，而在许多实际情况下，我们要考虑u所在类对X的隶属情况，这就成了变精度.以下定义在联系相似关系下的变精度.

定义7 设S为多值信息系统，∅≠B⊆A，∀X⊆U，0.5＜γ≤1，在联系度相似关系下的γ上、下近似分别为：

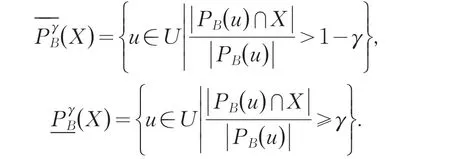
基于γ上、下近似得到的粗糙集模型称为γ变精度粗糙集模型.当γ=1时，因此，可看出γ变精度模型是更广的模型.

3 实例分析

以下用一个实例来比较分析多值信息系统集对联系度相似关系的粗糙集模型与相似关系、容差关系粗糙集模型之间的性能，说明多值信息系统集对联系度相似关系的粗糙集模型优于这两种集模型.

设多值信息系统S=〈U，A∪{d}〉，其中论域U={u1，u2，…，u6}，条件属性集A={a1，a2，…，a10}，d为决策属性，见表1.

表1 多值信息系统Tab.1Multi-value information system

用相似关系分析这个系统：

在这种分类中，u1与u3只有在属性a10取值不同就划在不同类中，导致了系统划分过细，特别不适合于对大型系统的处理.

用容差关系分析这个系统：

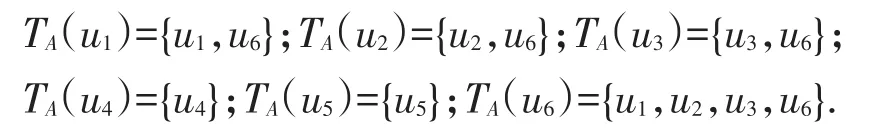
在这种分类中，u1与u6在属性a2，a6，a8，a10的取值都不可能相同却划在同类，使得划分很不合理，而且容易使系统划分过粗.

用联系度相似关系分析这个系统：取

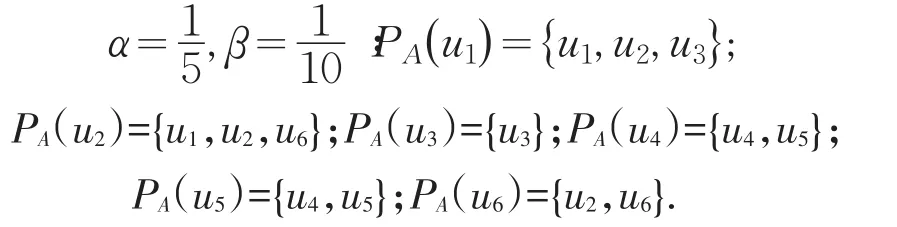
用这种关系分类，显然克服了以上两种关系的局限性.

4 小结

本文在多值信息系统下结合集对分析的思想，建立了集对联系度的粗糙集模型，这种模型既吸收了相似关系和容差关系模型的优点，又克服了它们的局限性，是比这两种模型更广的模型，还可根据实际运用的需要，对α，β合理的调节，达到对系统更灵活的处理.

[1]Pawlak Z.Rough sets[J].International Journal of Comput⁃er and Information Science,1982,11:341-356.

[2]Pawlak Z,Busse J G,slowinski R,et al.Rough sets[J].communications of the ACM,1995,38(11):89-95.

[3]王国胤.Rough理论与知识获取[M].西安:西安交通大学出版社,2001.

[4]张文修,仇国芳.基于粗糙集的不确定决策[M].北京:科学出版社,2005.

[5]王超,罗可.不完备信息系统中基于限制容差关系的属性约简方法[J].计算机应用,2011,31(12):3236-3239.

[6]陈家俊,苏守宝,金萍.一种对象完备度优先填补的决策树规则提取算法[J].计算机应用与软件,2014,31(5):264-267.

[7]舒畅.多值RS理论中属性约简的另一种算法[J].四川师范大学学报:自然科学版,2005,28(1):43-45.

[8]苏莉.基于条件信息熵的多值信息系统的属性约简[J].电脑学习,2010(6):106-107.

[9]吴根秀,王玏,纪军,等.多值信息系统的基于相似度的粗糙集模型[J].江西师范大学学报:自然科学版,2011,35(1):88-90.

[10]Kryszkiewicz M.Rough set approach to incomplete infor⁃mation system[J].Information Sciences,1998,11(2):39-49.

[11]赵克勤.集对分析及其初步应用[M].杭州:浙江出版社,2000.

[12]黄兵,钟斌,周献中.改进的集对粗集模型[J].计算机工程与应用,2004,40(2):82-84.

[13]刘富春.基于集对分析的变精度粗糙集模型[J].计算机工程与应用,2005,41(10):74-76.

[14]李长清,李克典.不完备信息系统下基于重要度相似关系的粗集模型[J].海南师范大学学报:自然科学版,2008,21(4):401-403.

[15]陈蓉素.不完备信息系统中的集对粗糙集模型分析[J].计算机工程与应用,2009,45(16):63-65.

[16]陈圣兵,李龙澍,纪霞,等.不完备信息系统中基于集对相似度的粗集模型[J].计算机科学,2010,37(7):186-190.

责任编辑：毕和平

Rough Set Model Based on Set-pair Analysis in Multivalude Information Systems

LI Changqing1，ZHANG Yanlan2
（1.School of Mathematics and Statistics，Minnan Normal University，Zhangzhou363000，China；2.College of Computer，Minnan Normal University，Zhangzhou363000，China）

In view of the limitations of similarity relation and tolerance in multivalude information systems,in the paper a new rough set model,set-pair connectivity rough set model,was proposed by introducting set-pair analysis.It generalized the two models above.

Multivalude information system；Similarity relation；Tolerance relation；Set-pair analysis；Connectivity simi⁃larity relation

TP 18

A

1674-4942(2015)02-0119-03

2015-03-08

福建省基金项目（2015J05011，JA14200，2013J01029，JA13198，JK2014028）