加筋板结构后极限强度行为影响参数研究
陈海龙,许维军,万乐天
(哈尔滨工程大学船舶工程学院,150001哈尔滨)
加筋板结构后极限强度行为影响参数研究
陈海龙,许维军,万乐天
(哈尔滨工程大学船舶工程学院,150001哈尔滨)
为使船体结构的安全性设计得到有效技术支撑,通过ABAQUS有限元软件,对面内压力作用下的加筋板结构进行响应分析,得出加筋板结构在达到极限强度之后的载荷-位移关系曲线,即后极限强度行为.探讨了板厚、材料硬化率、边界条件以及初始缺陷等影响船体加筋板结构受损之后承载能力的重要参数.结果表明:加强筋数量的增加对于提高加筋板结构在给定变形下的承载能力有利,板厚的增加并不能有效改善结构受损后的承载能力.
加筋板;后极限强度行为;载荷-位移关系;承载能力
加筋板结构在外载荷作用下的失效破坏往往会直接或间接地导致船体结构的失效破坏,在极限载荷作用下,加筋板结构一旦超过极限弯矩之后,其承载能力并非完全丧失,而是在一定程度上迅速下降,并随着塑性变形的增大而趋于平缓.加筋板结构的这种承载能力的变化正是该结构本构关系的体现,反映着结构在受损之后的承载能力随着变形程度的变化过程,通常可称这种变化过程为结构的后极限强度行为.
近年来,很多研究学者致力于研究加筋板结构的极限强度和结构发生屈曲之后的剩余强度研究.文献[1]采用ANSYS对加筋板结构进行有限元数值模拟研究,并与实验结果进行对比分析,结果发现采用SHELL43在有限元分析中能够很好地追踪加筋板结构的弹塑性行为的整个历程,分析结果与实验值吻合较好.文献[2]利用 LSDYNA分析船体梁模型在组合载荷作用下的极限强度和崩溃行为,文献[3]试验研究评估了箱型梁结构在遭受严重腐蚀后的极限强度问题.
文献[4-6]利用非线性有限元程序对“1/2+1+1/2跨距”的加筋板结构的极限强度进行了分析,总结在一个间距模型、“1+1间距”模型、“1/2+1+ 1/2间距”模型、“1+1+1间距”模型下筋的几何尺寸以及边界条件对加筋板的屈曲性能的影响.文献[7-8]基于可靠的应力分布状态利用改进的Paik-Mansour公式计算了箱型梁结构遭受垂向弯矩时的极限强度,并利用非线性有限元方法评估了焊接残余应力对于高强度钢结构在承受不同形式轴向压力下的极限强度,并研究探讨其中重要的影响参数.文献[9]则基于薄壁梁结构利用非线性数值方法研究了其在周期载荷作用下的极限强度,并分析了结构的累积塑性变形效应.文献[10]对破损舰船剩余承载能力进行了评估,采用Smith方法给出了一种基于材料机械特性、板厚尺寸、破口尺寸等多种不确定性因素的破损舰船剩余承载能力的计算方法.本文主要是通过数值模拟的手段,对加筋板结构在单向面内压力作用下的后极限强度行为进行研究,通过改变板厚、材料硬化率、边界条件以及初始缺陷等参数,探讨不同参数对加筋板结构的后极限强度行为的影响.
1 计算模型描述
船体结构在波浪载荷作用时的总纵强度一直受到研究学者的关注,尤其是波浪的波长与船体长度相当时,波浪弯矩与静水弯矩共同作用下易使船体多处于中垂或中拱状态.相比船体底部结构而言,甲板具有较小的刚度,距离船体剖面的中和轴较远,而且船用钢的抗拉伸性能要高于抗压缩性能,因此甲板结构更易于在波浪载荷作用下发生崩溃行为.所以本文选择船体结构处于中垂状态时,离中和轴较远的甲板结构作为研究对象,探索其在极限载荷作用下的后极限强度行为,旨在明确甲板结构在受损之后承载能力的变化过程,为船体结构的安全设计提供参考数据.在利用非线性有限元法分析船体加筋板极限强度时,面内载荷是最常见的形式,而弯矩对加筋板的作用通常可以等效为面内载荷作用,由于加筋板四周结构对其的约束,垂向载荷也使其产生面内的拉伸或压缩,因此本文只研究一般的面内载荷作用下加筋板架结构的后极限强度行为.首先,选择典型的甲板结构进行有限元建模,然后根据加筋板结构的受力特点施加轴向的面内压力,对该加筋板结构的承载能力进行数值计算和分析.文中有限元模型是基于典型的甲板板架结构建立的,见图1.加筋板结构的几何尺寸为:板长650 mm,宽650 mm,厚4、5、6、7 mm;加强筋腹板高30 mm,厚7 mm;加强筋翼板宽10 mm,厚7 mm.
2 有限元模拟
2.1 材料特性
计算模型所用材料为Q235钢,密度 ρ= 7 800 kg/m3,杨氏模量E=2.1×105MPa,泊松比ν=0.3.当加筋板结构在外载荷作用下发生崩溃时,非线性问题变得十分明显.为了简化,将材料的应力应变关系假设为满足线性硬化关系,从硬化率变化的角度探讨对结构后极限强度行为的影响.
2.2 初始缺陷
影响加筋板结构极限强度的初始缺陷主要为结构的初始变形与焊接残余应力,本文利用一致模态法加载模型的初始缺陷,根据文献[11]选用整体的变形模态来描述结构初始变形的影响.在模型数值计算中,仅考虑板的初始缺陷而假设加强筋在初始状态无弯曲和侧移缺陷,图2所示形状的模态作为初始缺陷的计算模态.缺陷因子为

式中:w为缺陷因子,代表加筋板的最大挠度;b1为加强筋之间的距离,取决于加强筋的数量.
2.3 边界条件和载荷
设置两种边界条件进行讨论,分别为简支及固支的边界条件.坐标系见图3,其中X轴沿加筋板宽度方向,即与加强筋方向垂直;Y轴则垂直于板架结构方向,Z轴沿加强筋长度方向,即平行于板面的方向.BC端完全固定,AD端沿X、Y方向限制位移,AB、CD端沿X方向限制位移;简支边界: BC端沿X、Y、Z方向限制位移,AD端沿X、Y方向限制位移,AB、CD端沿X方向限制位移.
本例中采用位移进行加载,轴向载荷施加AD边,见图3.在设置边界条件中,将产生位移的边或者节点预制为一定的位移,这样对应每个位移都会自动找到与之对应的载荷.这样的处理方式比直接施加力载荷的方式具有更大的优越性,可极大地降低收敛难度.在加筋板AD边界上设置沿Z轴方向的位移,限制边AB、CD横向即沿X轴的位移,输出BC边沿Z轴的支反力.值得注意的是,为准确地捕捉到板架结构发生崩溃时的瞬间行为,Z方向的位移不能设置太大,使结构能够在准静态状况下逐步达到崩溃即可.
2.4 网格划分及单元类型
有限元模型网格划分的疏密,对分析结果有较大的影响,尤其对于大挠度非线性问题.随着网格密度增加,分析结果会收敛到唯一解,但同时用于分析计算所需的时间也会增加.根据现有模拟条件以及模拟结果的精度要求,文中模型采用17 mm×17 mm的网格进行划分.本例中无论板还是加强筋都采用壳单元,网格单元采取壳单元常用的线性减缩积分四边形壳单元S4R.

图1 加筋板模型

图2 一致缺陷模态法确定的初始缺陷所用模态

图3 坐标系设置及加载方式
3 结果及分析
3.1 初始缺陷对加筋板结构后极限强度的影响
针对给定的计算模型,在简支条件下设置不同的初始缺陷,板厚取为4 mm,材料的硬化率取为E/40,对于加强筋数量取3、5、10时缺陷因子分别对应于0.81、0.54和0.29.在此条件下计算得出的载荷-位移曲线见图4,可看出,不同的初始缺陷对于结构的极限强度基本上没有影响,正如文献[12]中描述,不考虑初始缺陷加筋板结构的极限强度并不一定比考虑的大,还要取决于残余的拉应力是否可以抵消面内压载,而对后极限强度行为的影响却比较显著.缺陷因子的大小对应着初始变形的程度,因此从计算结果可知当缺陷因子为0.29和0.54时,结构的后极限强度行为相似,初始时开始出现“凸起”现象,然后沿着“凸起”处继续下降,最后趋于平缓.当缺陷因子为0.81时,结构的承载能力由极限强度点随着变形的增大急剧下降,并最后趋于平缓.3种不同的缺陷因子条件下结构的承载能力最后都基本上趋于相同的值.“凸起”现象的出现主要是由于在较小的初始缺陷条件下,结构在超过极限强度后承载能力迅速下降,应力进行重新分布,外力所做的功需要转化为塑形的应变能和部分的弹性应变能.能量在转化过程中试图寻找结构中的薄弱环节而进行转化,由于初始缺陷较小,使得能量在转化中首先会遇到一定的阻碍,当结构的变形变得稍微大一些时,能量的转化才变得容易.因此,缺陷因子为0.29、0.54所对应的载荷位移曲线中呈现出“凸起”的现象.而对于缺陷因子为0.81的情况下,结构具有较大的初始变形,能量在转化过程中能够很容易地沿着结构的薄弱环节转化为塑形应变能,不至于出现“凸起”现象.实际上加筋板结构受压发生屈曲时会沿着一个能量最小的平衡路径屈曲,当初始缺陷较小时,结构会沿着这个能量最小的平衡路径屈曲;当初始缺陷较大时,结构则会先沿着初始缺陷对应的模态发生屈曲现象.由于3种情况下的承载能力最终会趋于相同的值,可认为初始缺陷对于剩余强度的评估影响不大,而对于在给定变形情况下的承载能力评估结构有着显著的影响.由于缺陷因子与加强筋之间的距离有关,加筋板长宽一定时,加强筋数量的增加使加强筋间距减小,由式(1)可知,此时缺陷因子也相应减小.因此在控制重量的前提下,加强筋数量的增加对于提高加筋板结构在给定变形情况下的承载能力有利.
3.2 板厚对加筋板结构后极限强度的影响
在简支条件下,材料的硬化率保持E/40不变,加筋板结构的板厚变化为4~7 mm,得到不同板厚情况下的载荷-位移曲线见图5.可看出,随着板厚的增加,加筋板结构的初始刚度和极限强度有明显的提高,并且大致呈现线性增长.结构的承载能力在超过极限强度之后都表现为急速下降趋势.4 mm板厚的曲线呈现出明显的在开始阶段下降稍微平缓,然后出现较大的“凸起”现象,而5 mm板厚的曲线则下降急剧且比较光顺.板厚为6、7 mm的曲线也都表现为在承载能力下降的过程中出现了“凸起”现象,相比4 mm板厚,后两种曲线的“凸起”表现为较平缓,且随着板厚的增加“凸起”出现对应于的结构变形发生“后移”.4 mm板厚的情况发生在大约5 mm变形处,而6、7 mm板厚的情况分别对应于4、3 mm变形处.可认为加筋板结构在面内压力的作用下所表现出的本构关系不光与板厚有关,而且与加强筋的强度有关.载荷变形关系是结构的自身属性,可以称之为结构的本构关系,其不同于材料的本构关系.对于加筋板结构来说,当板厚较小时,加强筋的强度在承受载荷时占主导作用,加筋板结构的变形趋势与加强筋的变形趋势一致;而对于板厚较大的情形,板在承受载荷时占主导作用,加筋板结构的变形趋势与板的变形趋势一致.对于5 mm板厚的情形,则表现为板和加强筋在承受载荷作用时所起的作用相当.
另外,由于在模型计算中考虑了初始缺陷的影响,因此,在分析板厚对结构承载能力影响时不可忽略初始缺陷因素的影响.对于较小板厚的情况,加筋板结构在载荷作用下首先随着变形的增加试图寻找结构的最薄弱部位,在应力重新进行分配的过程中首先产生弹性大变形,由于初始缺陷的存在,最后会按照初始缺陷的模态产生塑性大变形.对于较大板厚的情况,结构的变形更容易遵循设定的初始缺陷模态发生.对于板厚为4 mm的情况,加强筋在板架结构中起到主要的承载作用,结构发生一定的大变形后才出现“凸起”现象;而对于6、7 mm时,板在板架结构中起到主要的承载作用,承载能力出现“凸起”所对应的变形明显前移,即按照给定的初始缺陷模态发生变形.对于板厚为5 mm的情况,作者认为由于板厚与加筋板尺寸之间处于一种中间的情形,板和加强筋在承载能力分配过程中都所起到的作用相当.这种情况下,加筋板结构在变形过程中更容易受初始缺陷的影响,结构的承载能力变化基本上是随着变形的增加急剧下降并最后趋于平缓.因此可认为,船体结构在设计阶段,合理地设计结构的尺寸对于提高结构的承载能力十分重要.
根据文献[13],定义结构的崩溃程度为

式中:Fu为极限强度,N;F0为承载能力下降之后最后趋于的平缓值,N.则不同板厚所对应的崩溃程度见图6.可看出板厚为5 mm的加筋板结构在受到极限载荷作用下的崩溃程度较高,反映出该结构受到初始缺陷的影响比较显著.对于7 mm板厚的加筋板结构,由于板厚的增加并没有降低结构的崩溃程度,可以认为板在承受载荷过程中并不能有效地改善结构的承载能力,加强筋才是提高结构承载能力的关键.另外,从结构的承载能力方面分析,将加强筋等效到板厚上在某种程度上意味着降低了结构在受损之后的承载能力.
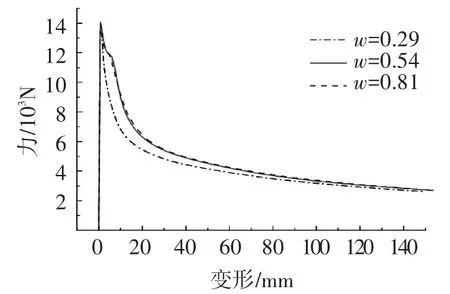
图4 不同缺陷因子下结构载荷-位移曲线

图5 载荷-位移曲线随厚度变化

图6 结构的崩溃程度随板厚的变化
3.3 硬化率对加筋板结构后极限强度的影响
以一组加筋板结构为例,探索不同硬化率对加筋板结构后极限强度的影响.板厚为7 mm,边界条件为简支,缺陷因子为0.81,硬化率从E/20变化到E/60.图7给出载荷-位移曲线随硬化率变化的规律.可看出硬化率对于结构的极限强度以及初始刚度基本上没有影响,但是对结构的后极限强度行为影响显著.随着硬化率的提高,结构的承载能力得到提高,这是由于硬化率越大的材料组成的加筋板结构所储存的应变能越大,同等变形情况下承载能力越大.因此,在船体结构设计时可考虑采用高硬化率的材料,这对于提高结构的承载能力是有利的.
3.4 边界条件对加筋板后极限强度的影响
为比较固支和简支两种边界条件对加筋板后极限强度行为的影响,将固支条件下的计算结果与图5中的计算结果汇总到一起,见图8.图中S.S代表简支,B.I代表固支.与图5中的结果对应,固支条件下的模型板厚变化也是从4~7 mm.从图8可看出,相同板厚的结构在简支边界条件下比固支条件下具有更大的极限强度和初始刚度;从结构的承载能力趋于平缓阶段来看,对于板厚为4、6和7 mm的结构,都呈现出简支条件下的承载能力高于固支条件的.然而,对于板厚为5 mm的情况却恰恰相反.可能是由于5 mm板厚的加筋板结构在承载外载荷时,由于板和加强筋所起到的作用相当,这种情况下,初始缺陷所对应的模态反而成为导致结构发生垮塌的主要因素.结构内部所贮存的内能会沿着初始缺陷所对应的模态释放能量,从而转化为塑性应变能.关于板和加强筋之间是否存在着某种刚度上的匹配,将有待于后续的研究和探索.

图7 载荷-位移曲线随硬化率变化
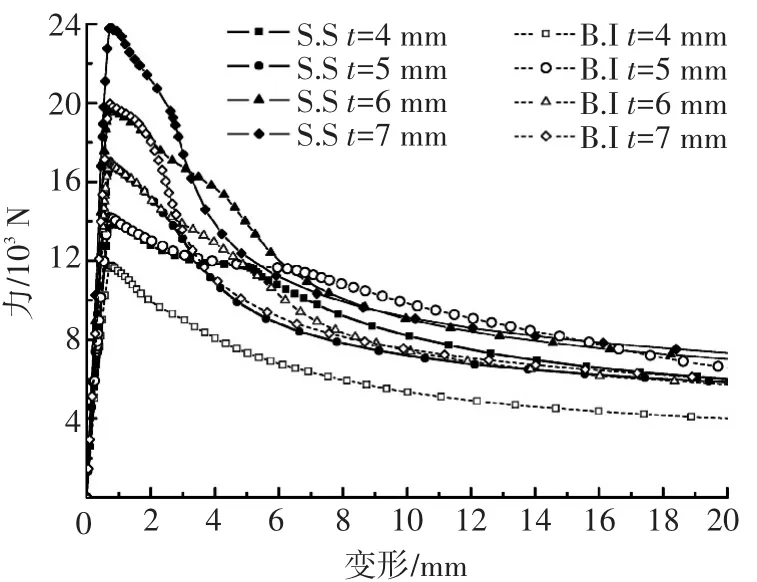
图8 简支和固支边界条件下的载荷-位移曲线
4 结 论
1)初始缺陷的存在会使受压加筋板结构载荷-位移曲线的后屈曲阶段出现“凸起”,大大提高了结构的后极限强度.加筋板长宽一定时,加强筋数量的增加使加强筋间距减小,此时缺陷因子也相应减小,在控制重量的前提下,对于提高加筋板结构在给定变形情况下的承载能力有利.
2)加筋板结构中板比较薄时承载能力的提高主要是加强筋起到主导作用,板比较厚时主要是板起到主导作用.加强筋承载能力的提高取决于板与加强筋的相对强弱,当二者之间存在着某种匹配时,初始缺陷起到了较大的作用,结构会沿着初始缺陷对应的屈曲模态产生变形.
3)板厚的增加在承受载荷过程中并不能有效地改善结构在受损后的承载能力,加强筋在提高结构承载能力过程中起到主导的作用.从结构的承载能力方面分析,将加强筋等效到板厚上在某种程度上意味着降低了结构在受损之后的承载能力.
4)在船体结构设计时可以考虑采用高硬化率的材料,这对于提高结构的承载能力是有利的.加筋板结构的后极限强度行为与边界条件有关,实际工程中该行为处于两种边界条件之间.
[1]GHAVAMI K,KHEDMATI M R.Numerical and experimental investigations on the compression behavior of stiffened plates[J].Journal of Constructional Steel Research,2006,62(11):1087-1100.
[2]TANAKA Y,ANDO T,ANAI Y,et al.Ultimate longitudinal strength of ships′hull girder under combined loading [J].Journal of the Japan Society of Naval Architects and Ocean Engineers,2012,16:121-130.
[3]SAAD-ELDEEN S,GARBATOV Y,SOARES C G.Experimental assessment of the ultimate strength of a box girdersubjected to severe corrosion[J].Marine Structures,2011,24(4):338-357.
[4]ZHANG S,KHAN I.Buckling and ultimate capability of plates and stiffened panels in axial compression[J].Marine Structures,2009,22(4):791-808.
[5]FUJIKUBO M,YAO T,KHEDMATI M R,et al.Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure part1: continuous plate[J].Marine Structures,2005,18(5):383-410.
[6]FUJIKUBO M,HARADA M,YAO T,et al.Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure part 2: continuous stiffened panel[J].Marine Structures,2005,18(5):411-427.
[7]PAIK J K,KIM D K,PARK D H,et al.Modified Paik-Mansour formula for ultimate strength calculations of ship hulls[J].Ships and Offshore Structures,2013,8(3/4): 245-260.
[8]PAIK J K,SOHN J M.Effects of welding residual stresses on high tensile steel plate ultimate strength:nonlinear finite element method investigations[J].Journal of Offshore Mechanics and Arctic Engineering,2012,134 (2):021401.
[9]CUI Huwei,YANG Ping,SEN Can,et al.Research on ultimate strength and accumulated plastic deflection of box beam under cyclic loading[J].Applied Mechanics and Materials,2014,496:567-570.
[10]任慧龙,李陈峰.破损舰船剩余承载能力分析[J].大连海事大学学报:自然科学版,2008,34(1):10-14.
[11]ZHANG Shengming,JIANG Lei.A procedure for nonlinear structural collapse analysis[C]//Proceedings of theASME 2014 33rd InternationalConferenceon Ocean,Offshore and Arctic Engineering OMAE2014,San Francisco,California,USA:OMAE2014-23397.
[12]XU Mingcai,SOARES C G.Ultimate strength of dented narrow stiffened panels subjected to compressive loads [C]//Proceedings of the ASME 2012 31st International Conference on Ocean,Offshore and Arctic Engineering OMAE2012,Rio de Janeiro,Brazil:OMAE,2012.
[13]XU Weijun,IIJIMA K,FUJIKUBO M.Parametric dependencies of the post-ultimate strength behavior of a ship's hull girder in waves[J].Journal of Marine Science and Technology,2012,17(2):203-215.
(编辑 苗秀芝)
Investigation into the influential parameters on post-ultimate strength behaviour of stiffened panels
CHEN Hailong,XU Weijun,WAN Letian
(College of Shipbuilding Engineering,Harbin Engineering University,150001 Harbin,China)
In order to provide the technical support for the safety of ship structure design,this paper focuses on the response of stiffened plate structure under in-plane compression by utilizing the nonlinear structural analysis code ABAQUS,once ultimate strength of the stiffened plate is reached,the load-displacement relationships,i.e.the post-ultimate strength behaviour can be obtained.Parametric dependencies of the postultimate strength behaviour of stiffened plates,such as geometric dimensions of plate,material parameters,initial imperfection and boundary conditions which influence the load carrying capacity are explored.Conclusions can be drawn:The increase of number of stiffeners is advantageous for enhancing the load carrying capacity of the structure when the deflection is assumed,and increasing of thickness of plate cannot effectively improve the load carrying capacity of the damaged structure.
stiffened plate;post-ultimate strength behaviour;load-displacement relationship;load carrying capacity
U663.2;TB303
A
0367-6234(2015)05-0118-05
10.11918/j.issn.0367-6234.2015.05.020
2014-06-30.
黑龙江省留学归国基金资助(LC2013C18);上海交通大学海洋工程国家重点实验室开放课题基金(1209);留学人员科技活动项目择优资助(工人函[2014]124号).
陈海龙(1981—),男,副研究员.
许维军,xuweijun@hrbeu.edu.cn.

