水下目标回波几何结构的时频域盲源分离
孙世钧,李秀坤,孟祥夏
(哈尔滨工程大学水声技术国家级重点实验室,黑龙江哈尔滨150001)
主动声呐对水下目标进行探测时,目标的声散射信号回波中携带着目标的重要信息,如目标的几何形状、尺度和材质信息等,这些信息是对目标进行识别和作进一步分析的基础。汤渭霖[1]于1994年提出了声呐目标回波亮点模型,将水下目标回波分解为多个亮点的线性叠加。1998-2000年,Azimi-Sadjadi[2-3]等人采用小波变换对水下沉底目标进行了分类与识别。2000年以来,李秀坤[4-6]等人运用多种方法对水下目标的亮点结构进行了特征提取,文献[7-8]运用盲源分离的方法将混响与目标回波进行分离。然而,在国内外研究成果中,很少对于回波信号亮点之间的分离方法进行论述。
盲源分离(blind sources separation,BSS)是20世纪80年代中后期迅速发展起来的一种信号处理方法。它可以在源信号及传输通道特性事先未知的条件下从若干观测到的混合信号中提取、分离出无法直接观测的各个原始信号,只要源信号之间满足相互独立或不相关的条件。由于盲源分离算法的不确定性[9],将导致分离信号的幅度和排列顺序与源信号不同,但这种不确定性不会影响对信号的分析。对于非平稳源信号的分离问题,常采用时频域盲源分离方法[10]。本文利用回波信号中的各个亮点结构在时频域上具有不同分布的特点,采用时频域盲源分离方法对回波信号进行分离,可以很好地将各个亮点分离开。
1 目标回波的亮点模型
理论分析和实验都证明,在高频情况下,任何一个复杂目标的回波都是由若干个子回波叠加而成的,每个子回波可以看成是从某个散射点发出的波,这个散射点被称为亮点。根据亮点的产生机理的不同,可以分为几何亮点和弹性亮点2大类:1)几何亮点:由目标几何形状决定的回波称为几何反射波,相应的回波称为几何类亮点。这类亮点的声中心就是几何上的凸点、棱角等。2)弹性亮点:当入射声波与目标的本征频率相吻合时,目标将产生共振振动向周围介质辐射声波,称之为弹性再辐射回波或弹性类亮点。这些波的传播速度、衰减及再辐射效率与材料参数及物体形状有关,由文献[1]可知,这类亮点的声中心并不对应真实的几何亮点,而是根据波传播的声程确定的等效亮点。
当回波信号中存在N个亮点时的系统函数为

式中:A(r,ω)是幅度因子,τ是时间延迟因子,φ是相位跳变因子。
2 基于亮点模型的时频域盲源分离方法
假设发射信号为线性调频信号,回波信号中包含n个几何亮点结构。若将这n个几何亮点视为源信号,则

式中:f0是线性调频信号的初始频率,k是线性调频信号的调频斜率,An、τn、φn分别为源信号的幅度、相对于发射信号的时间延迟和相位变化。由线性调频信号可知,n个亮点在时频二维平面上可以由n条相互平行的斜线来表示。
n个源信号通过混合矩阵H混合后得到n个观测信号(假定观测信号与源信号的数目相同)x(t),则对x(t)进行时频域盲源分离的算法如下:
1)对观测信号x(t)进行白化处理,得到白化矩阵W,进而得到白化信号:

2)对白化信号z(t)进行WVD时频变换,得到白化信号的WVD时频分布矩阵:
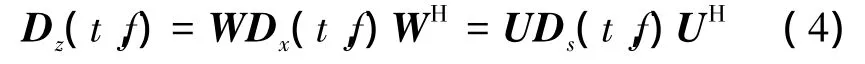
其中,U代表酉矩阵,Ds为源信号的WVD时频分布矩阵,即

式中:

当i=j时,dij表示第i个源信号的WVD分布,称为信号的自项;当i≠j时,dij表示第i个源信号和第j个源信号的互WVD分布,称为信号的互项。若Ds为一对角阵,则可以得到
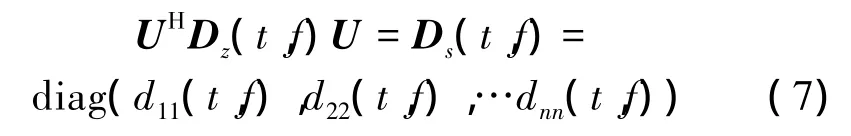
式(7)说明:白化信号时频分布函数矩阵可以被一个酉矩阵变换为对角阵,只要找到一个酉阵使分布函数矩阵Dz(t,f)对角化就实现了混合矩阵的盲辨识。
3)正确地选择时频点。因为在某些时频点上Ds主对角线的元素值不大于其他位置元素的值,就不能认为Ds近似为对角阵。例如由于WVD分布会引起交叉项,对于交叉项能量集中的时频点,分布矩阵互项的元素值远大于在该时频点上自项的元素值。所以正确地选择时频点对恢复源信号起到了关键性作用。时频点的选择方法如下:
首先,对于时频面上每一个(t,f)点对应的矩阵Dz(t,f)求迹,得到
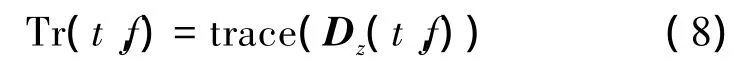
通过上述选择时频点的方法,可以将亮点结构所在的时频点选出,而将其相互交叉项的时频分布点去除。
4)采用以下时频对角化对照函数,运用联合对角化的方法求出酉矩阵。

其中,off()为非对角线元素的平方和。
5)通过式(10)求得各个亮点源信号的时域信号。

3 仿真分析
为了验证本文所述方法的有效性,下面对含有2个几何亮点的信号进行时频域盲源分离仿真研究(对采样频率进行归一化处理)。
仿真1 假设主动声呐发射信号为线性调频脉冲信号,脉冲持续时间为1 000 s。回波信号中包含2个几何亮点。模拟亮点源信号为2个线性调频脉冲信号,起始频率和截至频率分别为f1=0.04 Hz,f2=0.09 Hz,幅度分别为 1、0.2,2 个几何亮点的时间延迟分别为200、400 s,信号的采样频率fs=1 Hz。假定源信号通过随机混合矩阵A=rand(2,2)进行混合,各传感器得到的观测信号及其Wigner-Ville时频分布如图1所示。运用时频域盲源分离方法对观测到的混合信号进行分离,得到的分离信号及其与发射信号的匹配滤波如图2所示。

图1 各路观测信号的时域图及其时频分布Fig.1 The observed signals in time domain and time-frequency domain
从图1、2中可见,观测信号是2个亮点源信号在时域上的混合信号,由于2个亮点的幅度相差较大,在观测信号的时频分布图上仅能观测到第1个亮点信号及其与第2个亮点信号的交叉项,第2个亮点信号的时频特性被淹没。经过时频域盲源分离算法处理后,2个几何亮点在时域上可以被分离。
仿真2 假设主动声呐发射信号为线性调频脉冲信号,脉冲持续时间为1 000 s。回波信号中包含2个几何亮点。模拟亮点源信号为2个线性调频脉冲信号,起始频率和截至频率分别f1=0.04 Hz,f2=0.09 Hz,幅度均为1,2个几何亮点的时间延迟分别为200、250 s,即亮点间的时间延迟为τ=50 s,信号的采样频率fs=1 Hz,假定源信号通过随机混合矩阵A=rand(2,2)进行混合,各传感器得到的观测信号及其Wigner-Ville时频分布如图3所示。运用时频域盲源分离方法对观测到的混合信号进行分离,得到的分离信号及其与发射信号的匹配滤波如图4所示。改变第2个几何亮点的时间延迟为230 s,各传感器得到的观测信号及其Wigner-Ville时频分布如图5所示,得到的分离信号及其与发射信号的匹配滤波如图6所示。

图3 τ=50 s时观测信号的时域图及其时频分布Fig.3 The observed signals in time domain and time-frequency domain when τ=50 s

图4 τ=50 s时分离信号的时域图及其匹配滤波Fig.4 The separated signals in time domain and its matched filtering when τ=50 s

图5 τ=30 s时观测信号的时域图及其时频分布Fig.5 The observed signals in time domain and time-frequency domain when τ=30 s

图6 τ=30 s时分离信号的时域图及其匹配滤波Fig.6 The separated signals in time domain and its matched filtering when τ=30 s
由图3~6可见,当2个几何亮点之间的时间延迟较小时,由于Wigner-Ville分布时频分辨率的限制,不能在时频图上将2个亮点区分开。当时间延迟为50 s时,通过时频域盲源分离算法可以将2个亮点分离开。当2个几何亮点之间的时间延迟减小为30 s时则不能通过该算法将2个亮点在时域上进行分离。2个几何亮点之间不同时间延迟下的相关系数如图7所示。

图7 2个亮点不同时延下的相关系数Fig.7 Correlation coefficient of highlights with different time delays
由图7可见,随着2个亮点之间时间延迟的增大,其相关系数逐渐减小。当相关系数小于0.2时,2个亮点可以通过时频域盲源分离方法在时域上分离开来,当相关系数大于0.2时则不能分离。
4 实验数据处理分析
实验环境:实验在某消声水池中进行,将圆柱形目标用吊绳悬浮在水池中,如图8所示,用发射换能器发射线性调频脉冲信号,发射信号归一化频率范围为0.02~0.08 Hz,脉冲宽度为 1 000 个采样点。采用2阵元组成的线阵进行信号接收。转动目标,得到不同掠射角下接收到的观测信号,并采用本文所述方法对观测信号进行分离。
当掠射角分别为 0°、90°、180°时,得到的观测信号及其时频分布图、分离信号及其时频分布图如图9~14所示。从图9~14可见,当掠射角为90°、180°时,可以通过时频域盲源分离方法将混合信号中的2个亮点进行分离。当掠射角为0°时,从水听器接收到混合的观测信号的时频分布图上仅能观测到一个亮点,经过时频域盲源分离后,虽然不能够在时域上将2个亮点进行分离,但是可以从分离后一路信号的时频分布上观测到第2个亮点,说明在这路分离信号中第2个亮点的相对能量被增强了。

图8 目标模型图Fig.8 Target model

图9 掠射角为0°时观测信号及其时频分布Fig.9 The observed signals in time domain and time-frequency domain with grazing angle 0°

图10 掠射角为0°时分离信号及其时频分布Fig.10 The separated signals in time domain and time-frequency domain with grazing angle 0°

图11 掠射角为90°时观测信号及其时频分布Fig.11 The observed signals in time domain and time-frequency domain with grazing angle 90°

图12 掠射角为90°时分离信号及其时频分布Fig.12 The separated signals in time domain and time-frequency domain with grazing angle 90°

图13 掠射角为180°时观测信号及其时频分布Fig.13 The observed signals in time domain and time-frequency domain with grazing angle 180°

图14 掠射角为180°时分离信号及其时频分布Fig.14 The separated signals in time domain and time-frequency domain with grazing angle 180°
5 结论
本文采用一种基于时频域盲源分离的方法对主动声呐回波信号中的亮点结构进行分离,通过理论推导、仿真分析及实验数据的处理,得到如下结论:
1)基于水下目标的亮点模型,将每个亮点视为源信号的一个向量,然后采用时频域盲源分离算法进行分离,通过合理地选择时频点,抑制了源信号的交叉项,使信号的能量集中在其时频分布矩阵的主对角线上。
2)在仿真分析中改变2个亮点间的时间延迟,当2个亮点之间的相关系数小于0.2时,可以通过时频域盲源分离方法将其进行分离,大于0.2时则不能分离。
3)在仿真分析中改变2个亮点间的相对幅度,当2个亮点之间的的相对幅度差别较大时,幅度较小的亮点在观测信号的时频分布图中被淹没,这时可以通过时频域盲源分离方法将其进行分离。
4)通过水池实验,验证了该方法分离水下目标回波亮点结构的可行性。当掠射角为90°、180°时,可以将回波中的2个亮点分离开;当掠射角为0°时,提取到了被淹没在混合信号中的第2个亮点的时频特征。
[1]汤渭霖.声呐目标回波的亮点模型[J].声学学报,1994,19(2):92-100.TANG Weilin.Highlight model of echoes from sonar targets[J].Acta Acustica,1994,19(2):92-100.
[2]AZIMI-SADJADI M R,CHARLESTON S,WILBUR J,et al.A new time delay estimation in subbands for resolving multiple specular reflections[J].IEEE Transactions on Signal Processing,1998,46(12):3398-3403.
[3]AZIMI-SADJADI M R,YAO De,HUANG Qiang,et al.Underwater target classification using wavelet packets and neural networks[J].IEEE Transactions on Neural Networks,2000,11(3):784-794.
[4]李秀坤.水雷目标特征提取与识别研究[D].哈尔滨:哈尔滨工程大学,2000:1-120.LI Xiukun.Research on extracting and recognizing of mine character[D].Harbin:Harbin Engineering University,2000:1-120.
[5]李秀坤,李婷婷,夏峙.水下目标特性特征提取及其融合[J].哈尔滨工程大学学报,2010,31(7):903-908.LI Xiukun,LI Tingting,XIA Zhi.Feature extraction and fusion based on the characteristics of underwater targets[J].Journal of Harbin Engineering University,2010,31(7):903-908.
[6]LI Tingting,LI Xiukun,XIA Zhi.Classification of underwater mines by means of the FRFT and SVM[C]//Proceedings of the 2010 IEEE International Conference on Information and Automation.Harbin,China,2010:1824-1829.
[7]LI Xiukun,WANG Qiyong.Blind separability of reverberation and target echo based on spatial correlation[C]//4th International Conference on Measuring Technology and Mechatronics Automation.Sanya,China,2012:538-543.
[8]李雯雯.混响背景下盲分离方法的研究[D].哈尔滨:哈尔滨工程大学,2013:1-59.LI Wenwen.Research on blind source separation in reverberation background[D].Harbin:Harbin Engineering University,2013:1-59.
[9]马建仓,牛奕龙,陈海洋.盲信号处理[M].北京:国防工业出版社,2006:23-24.
[10]BELOUCHRANI A,AMIN M G.Blind source separation based on time-frequency signal representations[J].IEEE Transactions on Signal Processing,1998,46(11):2888-2897.

