多气泡耦合作用下非球状特性数值研究

姜忠涛，韩蕊，李帅

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

气泡在工程领域得到了人们广泛的关注，用以探测石油的高压气枪、军事中造成舰船毁伤的水下爆炸气泡、螺旋桨产生的空泡，这一切都与气泡的动力学特性有着密不可分的关系。从 Rayleigh(1917)［1］对球状脉动气泡的理论研究开始，人们开展了大量有关气泡动力学的研究工作，目前国内外学者在数值和实验研究方面也取得了丰硕的成果［2-6］，而在数值研究方面，基于势流理论的边界元方法由于其高效、高精度的优势得到了广泛应用。对于单气泡的研究，学者模拟了气泡与自由液面［2，7-9］、刚性壁面［10］等不同边界的相互作用，并且对射流后的环状气泡也进行了数值模拟［11-12］;而随着研究的深入，很多学者对2个气泡与自由液面［13-14］、刚性壁面［15］的工况也进行了研究，Fong 等人(2008)［16］通过电火花实验对气泡相位差、气泡间距联合作用下2个气泡相互作用的不同现象进行了图表总结，同时采用边界元方法只对3个气泡相互作用的几个典型工况进行了数值模拟。研究3个气泡相互作用的公开文献还较少，这主要是由于气泡运动与气泡间距、初始条件、排列方式、相位等多因素有关［16］，其中较基础的研究是垂向布置的3个同相气泡间的相互作用。

本文基于势流理论，建立了边界元数值模型，对3个气泡的相互作用进行数值模拟。首先，将数值结果与球状脉动气泡解析解进行对比，验证了数值模型的有效性和收敛性，然后研究垂向布置的3个同相气泡的耦合特性，主要分析气泡间距对气泡运动的影响，分别探讨了等间距和不等间距布置气泡工况中气泡的运动规律和机理，旨为研究多气泡相互作用的研究提供一定的参考。

1 边界元基本理论

本文基于势流理论，建立轴对称数值模型模拟垂向布置的3个同相气泡间的相互作用，由于气泡运动过程中，气泡表面速度维持在比水中声速小一些的量级上，且雷诺数高、持续时间短，故可忽略可压缩性和粘性耗散。因此，认为流体不可压缩、无粘、无旋，速度势在流域内满足拉普拉斯方程以及边界积分方程:

式中:p是边界上控制点;ω-为在该点观察流场的立体角，此处=2π;q则为是边界上积分点;G(p，为自由空间格林函数;n是指向流场外(气泡内部)的法向量，法向导数定义为为流体域的所有边界，在本文中所有边界由3个气泡的表面组成。

由于气体和水的密度巨大差异，所以在本文中假设气泡内气体运动对压力的影响可忽略不计;同时由于气泡运动的瞬态特性，故可忽略热交换效应，基于绝热假设，气体压力仅和气泡初始状态及其体积有关，则每个气泡外表面水的压力均满足［12］:

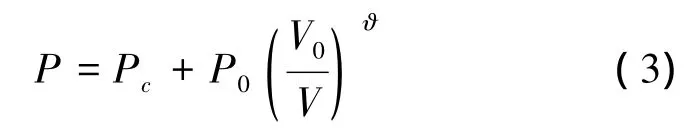
式中:Pc为气泡内可冷凝气体的饱和蒸汽压;下标“0”表示气泡初始状态(初始压力和体积);ϑ为气体的比热，和气体组成有关，本文中 ϑ 取 1.25［6，17〛。

气泡表面的动力学边界条件为

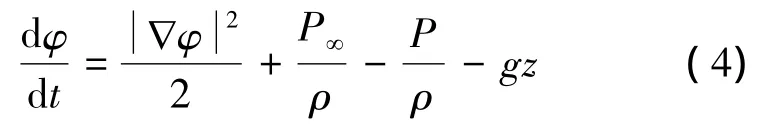
式中:P∞为静水压力，ρ为流体密度，g为重力加速度，z代表位置矢量的垂直分量。

研究过程中，采用气泡最大半径Rm、ΔP=P∞-Pc分别作为长度、压力的特征量，相应地以Rm(ρ/ΔP)1/2、Rm(ΔP/ρ)1/2以及 (ρgRm/ΔP)1/2对时间、速度势和浮力进行无量纲化，则得到式(4)的无量纲形式为［18］

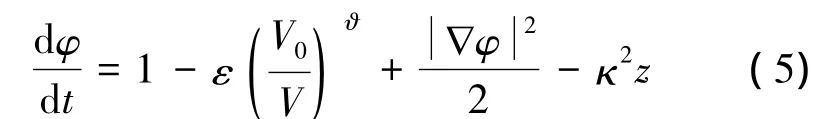
式中:ε=P0/ΔP为气泡强度参数为浮力参数，本文中κ=0。同时，对于本文中研究的3个气泡相互作用，如图1垂向布置3个气泡，则分别定义d1=D1/Rm和d2=D2/Rm为气泡1、2和气泡2、3之间的间距参数，D1和D2为相应的气泡中心间距，在等间距工况中间距参数满足d1=d2=d。另外，下文中出现的其他无量纲变量还包括时间T、气泡半径R、射流速度vjet和气泡体积V。图1中参数R0为气泡的初始半径，可由下式确定［19］:

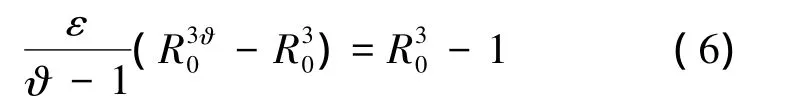
气泡的运动学边界条件为［11］

数值求解方程(2)的具体细节可参考文献［19］，根据式(2)求得的速度，联立式(5)和式(7)，则可对气泡表面的速度势及位置进行更新。计算过程中采用二阶龙格-库塔沿时域向前推进，且为维持计算过程的稳定，每一时间步长均需严格控制，使得每个节点的速度势在每一步的改变量不会超过Δφ(Δφ为某一常数)，其取值将在下文进行讨论说明。

图1 气泡布置及间距定义Fig.1 Bubble arrangement and the definition of inter-bubble distance

2 数值结果

2.1 数值模型有效性验证

本文建立边界元模型研究多气泡的耦合特性，在此之前需要验证数值模型的有效性。在本文中，首先采用Rayleigh-Plesset方程(R-P方程)描述无重力自由场中的球形气泡的运动，R-P方程的无量纲形式为［1］

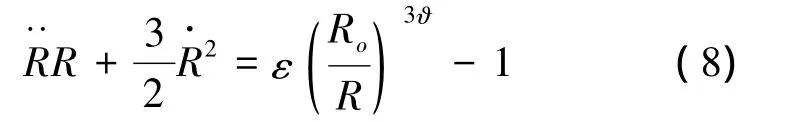
选取工况为 ε=60，R0=0.178 8，κ=0，采用四阶龙格-库塔求解，可得到球形气泡半径时历变化曲线。同时，用本文的边界元模型对相同工况下球形气泡的运动进行计算，将得到的结果与R-P方程对比，如图2所示。图2(a)和图2(b)分别给出了节点数和ΔΦ的改变对计算结果的影响，观察发现数值结果与R-P方程解析解均吻合良好。在不考虑重力作用的自由场中，气泡的最大半径理论值为1，分别列出不同节点数和Δφ的计算结果、相对误差及计算时长，见表1、表2。

由表1可知，当气泡节点数增加至30以上时，最大半径Rm的误差已减小至0.1%以下，随着节点数的增加，计算时长增加;由表2可知，当Δφ≤0.03(节点数为50)时，计算误差都能保持0.05%以内，随着Δφ的减小，计算精度提高并不明显，但计算时长明显增加。

图2 气泡半径时历变化曲线数值结果与解析解对比Fig.2 Comparison of the bubble radius history of the BEM model with the analytical solution

表1 不同节点数的计算精度及效率Table 1 Effect of nodes number on the calculation accuracy and efficiency

表2 不同Δφ的计算精度及效率Table 2 Effect of Δφ on the calculation accuracy and efficiency

通过图2曲线对比和表1、表2的数据可验证本文数值模型的有效性，同时，数值模型的收敛性也可以得到保证。在下文数值算例中，选择节点数50和Δφ=0.02以平衡计算精度和计算效率(计算时长)。

2.2 数值算例

数值模拟3个同相气泡间的耦合特性，3个初始条件相同的气泡垂向排列，初始参数均为ε=60，R0=0.1788，κ =0，每个气泡表面采用 50 节点，取Δφ=0.02，分别对等间距和不等间距的情况进行计算分析。

图3 不同d下，射流完成时气泡形态Fig.3 Bubble profiles upon the impact with different d

首先研究等间距情况，即d1=d2=d。由于气泡间距过小时，气泡会发生融合的现象，而间距过大时则气泡间影响不明显，故本文中气泡间距的变化范围取为［1.8，5.0］。当气泡间距d发生变化时，气泡射流完成时的形态也会有所不同，如图3所示。观察发现，当d=1.8时，3个气泡的相邻位置在很大范围内均发生扁平的现象，气泡2更呈现出“圆柱状”，且其中间部分出现向内的凹陷;d=2.0工况中的气泡形态与上一工况相似，只是扁平范围较小且气泡2较“瘦长”;当气泡间距d继续增大时，可以发现气泡1和3在射流完成时的体积减小，且被射流冲击区域已不再扁平，而气泡2也已呈现“椭球状”并逐渐趋于球形，同时中间位置也不再出现凹陷。为了更准确地分析气泡形态的变化，计算不同d对应的气泡1射流速度时历曲线、气泡1体积变化和气泡2体积变化，如图4～6所示。

由于气泡1、3的运动相同，其形态以气泡2为中心对称，所以只给出气泡1的计算结果。由图4的射流速度时历曲线可了解到气泡的运动过程，图中实线为射流点(气泡1顶点)速度、虚线为被射流冲击点(气泡1最低点，与气泡2相邻点)速度，气泡首先快速膨胀，随着内部压力的减小，膨胀速度变慢、膨胀运动减缓，可以观察到膨胀阶段气泡基本保持球形;当膨胀到某个时刻，膨胀停止，紧接着气泡快速收缩，由于周围另一气泡的影响，气泡上、下两部分收缩程度不同，随着收缩的进行，气泡1形成向下的射流，同时可观察到，气泡收缩速度在其后期变慢，这主要是由于气泡收缩导致内压增大，从而收缩运动受到阻碍。观察图4射流速度受d影响的变化规律:d不同，射流点速度在坍塌阶段后期有所不同，随着d的增大，气泡射流点速度在后期增加越快、射流完成时速度越大;随着d的增大，气泡被射流冲击点的膨胀速度减小得慢，坍塌阶段收缩速度快(如图5所示，气泡1达到的最大体积变大，但体积减小速度快，从而射流完成时间早)，但受内压影响较大，导致坍塌后期收缩速度减小，尤其d∈［3.0，5.0］范围内收缩速度减小十分明显。由以上叙述可知，当气泡周围存在另一气泡时，其运动将受到抑制，从而气泡能到达的最大体积变小，但其收缩速度受到的抑制导致气泡射流完成得晚。以同样的原因分析气泡2的体积变化，观察图6发现，d较小时，气泡2受到来自上、下方气泡的抑制，其膨胀速度慢，但气泡2在此作用下形状会发生变化，呈现出被拉长的“椭球状”或上下端扁平的“圆柱状”，故膨胀阶段气泡2能够达到的最大体积增大，但d对接下来的收缩速度影响不大。由此可知，多气泡间存在抑制作用，从而影响其膨胀和收缩速度，这种速度的不同将导致气泡形态发生变化。

接下来研究不等间距情况，即d1≠d2，且由于本文设置初始参数下气泡1、3形态、运动的对称性，故只需研究d1≤d2的情况。为避免融合现象的发生，不等间距情况的研究中d1∈ [1.8，5]且d1+d2=10，在此间距组合下，由以上分析可知气泡1的运动受到抑制，计算在气泡3完成射流时刻停止，故图7给出气泡3的射流速度时历曲线，同时给出气泡1和气泡3体积变化以及气泡2体积变化，如图8、9所示。图7、图8中的变化规律与等间距分析的结果相同，在此不再赘述:仔细观察图7可发现被射流冲击点(气泡3顶点)的速度在坍塌阶段后期减小十分明显，与等间距情况中d∈［3.0，5.0］的变化类似，说明气泡3已经开始发生回弹(图8中气泡3体积变化曲线已经开始上升);观察图8可知，随着d1，d2差距的减小，气泡1和气泡3体积变化曲线均向d1=d2=5.0的气泡1体积变化曲线移动，说明了该数值模型和变化规律的收敛性。图9给出了气泡2的体积变化曲线，可以发现d1，d2的变化对气泡2达到的最大体积影响不大，而随着d1的减小和d2的增大，气泡2的膨胀、收缩速度都增大。

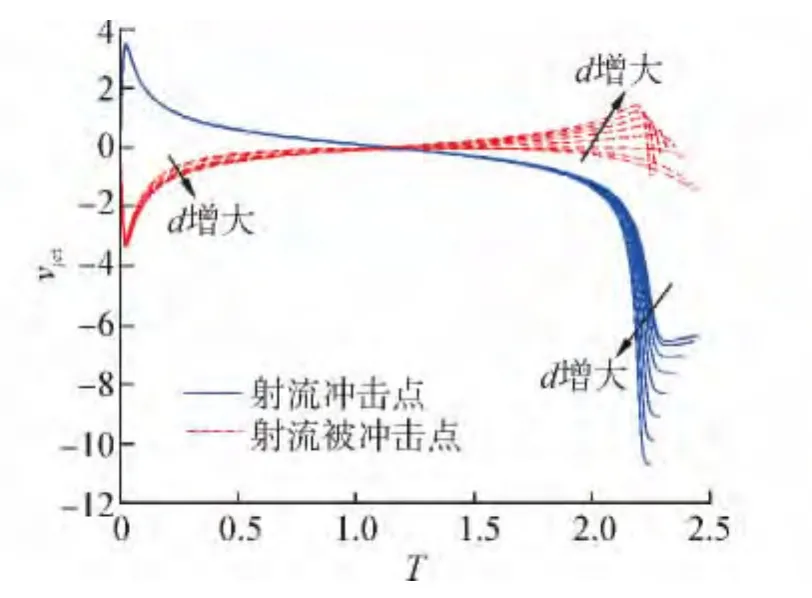
图4 气泡1射流速度时历曲线Fig.4 Time-history of the jet velocity of bubble 1

图5 气泡1体积变化Fig.5 Time-history of the volume of bubble 1

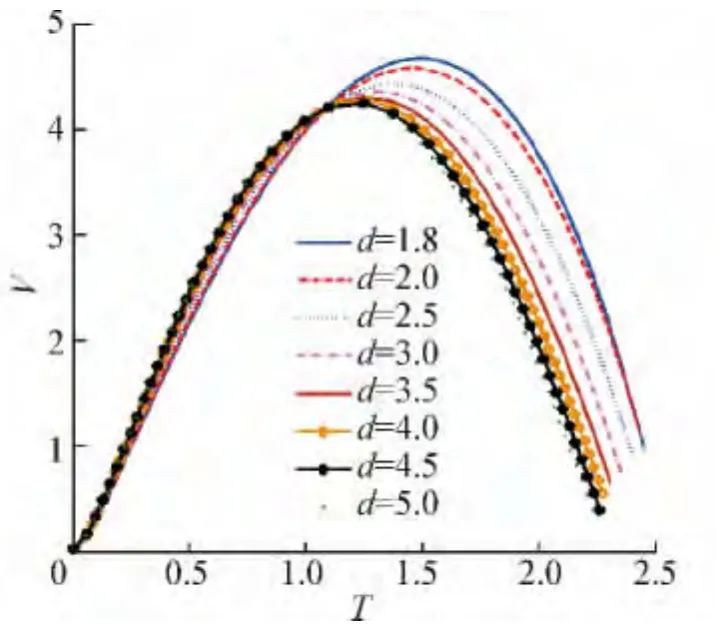
图6 气泡2体积变化Fig.6 Time-history of volume of bubble 2

图7 气泡3射流速度时历曲线Fig.7 Time-history of the jet velocity of bubble 3

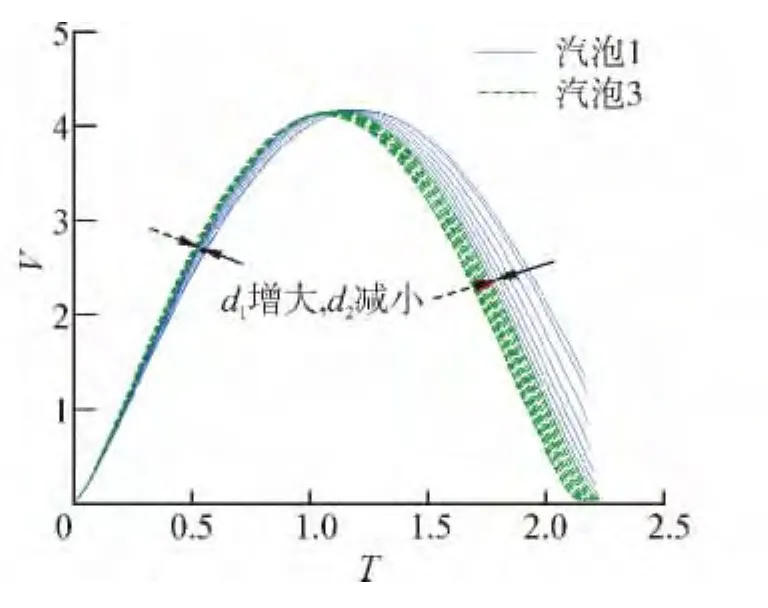
图8 气泡1和气泡3体积变化Fig.8 Time-history of the volume of bubble 1 and bubble 3

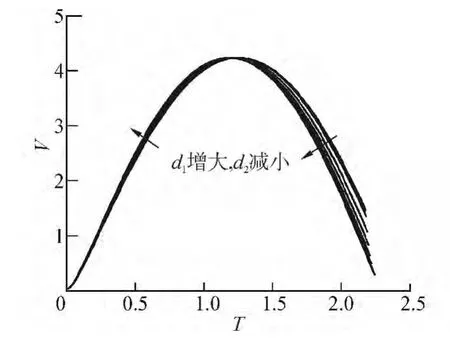
图9 气泡2体积Fig.9 Time-history of the volume of bubble 2

3 结论

1)多气泡间存在抑制作用，垂向等间距布置的3个气泡，上、下两端气泡会出现射流现象，中间气泡则在两端气泡的影响下呈现出“圆柱状”或“椭球状”，若间距足够大则趋于球形脉动。

2)3个同相气泡垂向等间距布置，随着d的增大，上、下两端气泡能达到的最大体积越大，但完成射流越早，而随着d的增大中间气泡能够达到的最大体积越小。

3)在不等间距布置气泡的情况下，最下方气泡(与中间气泡间隔远)首先发生射流，随着中间气泡不断向下移动，下方气泡的膨胀、收缩运动均受到阻碍，而中间气泡的膨胀、收缩速度都变大，但其最大体积变化不明显。

［1］RAYLEIGH L.VIII.On the pressure developed in a liquid during the collapse of a spherical cavity［J］.Philosophical Magazine Series 6，1917，34(200):94-98.

［2］BLAKE J R，GIBSON D C.Growth and collapse of a vapour cavity near a free surface［J］.Journal of Fluid Mechanics，1981，111:123-140.

［3］WANG Q X，YEO K S，KHOO B C，et al.Vortex ring modelling of toroidal bubbles［J］.Theoretical and Computational Fluid Dynamics，2005，19(5):303-317.

［4］KLASEBOER E，HUNG K C，WANG C，et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure［J］.Journal of Fluid Mechanics，2005，537:387-413.

［5］ZHANG Aman，YANG Wenshan，HUANG Chao，et al.Numerical simulation of column charge underwater explosion based on SPH and BEM combination［J］.Computers＆ Fluids，2013，71:169-178.

［6］ZHANG Aman，WANG Shiping，HUANG Chao，et al.Influences of initial and boundary conditions on underwater explosion bubble dynamics［J］.European Journal of Mechanics-B/Fluids，2013，42:69-91.

［7］BLAKE J R，TAIB B B，DOHERTY G.Transient cavities near boundaries.Part 2.Free surface［J］.Journal of Fluid Mechanics，1987，181:197-212.

［8］WANG Q X，YEO K S，KHOO B C，et al.Strong interaction between a buoyancy bubble and a free surface［J］.Theoretical and Computational Fluid Dynamics，1996，8(1):73-88.

［9］李帅，张阿漫，王诗平.气泡引起的皇冠型水冢实验与数值研究［J］.物理学报，2013，62(19):194703.LI Shuai，ZHANG Aman，WANG Shiping Experimental and numerical studies on“crown”spike generated by a bubble near free-surface［J］.Acta Physica Sinica，2013，62(19):194703.

［10］LI Shuai，LI Yunbo，ZHANG Aman.Numerical analysis of the bubble jet impact on a rigid wall［J］.Applied Ocean Research，2015，50:227-236.

［11］BEST J P.The formation of toroidal bubbles upon the collapse of transient cavities［J］.Journal of Fluid Mechanics，1993，251:79-107.

［12］WANG Q X，YEO K S，KHOO B C，et al.Nonlinear interaction between gas bubble and free surface［J］.Computers＆ Fluids，1996，25(7):607-628.

［13］ROBINSON P B，BLAKE J R，KODAMA T，et al.Interaction of cavitation bubbles with a free surface［J］.Journal of Applied Physics，2001，89(12):8225-8237.

［14］HAN Rui，ZHANG Aman，LI Shuai.Three-dimensional numerical simulation of crown spike due to coupling effect between bubbles and free surface［J］.Chinese Physics B，2014，23(3):034703.

［15］BLAKE J R，ROBINSON P B，SHIMA A，et al.Interaction of two cavitation bubbles with a rigid boundary［J］.Journal of Fluid Mechanics，1993，255:707-721.

［16］FONG S W，ADHIKARI D，KLASEBOER E，et al.Interactions of multiple spark-generated bubbles with phase differences［J］.Experiments in Fluids，2009，46(4):705-724.

［17］李章锐，宗智，董婧，等.两个气泡相互作用的某些动力特性研究［J］.船舶力学，2012，16(7):717-729.LI Zhangrui，ZONG Zhi，DONG Jing，et al.Some dynamic characteristics of the interactions of two bubbles［J］.Journal of Ship Mechanics，2012，16(7):717-729.

［18］WANG C，KHOO B C.An indirect boundary element method for three-dimensional explosion bubbles［J］.Journal of Computational Physics，2004，194(2):451-480.

［19］KLASEBOER E，HUNG K C，WANG C，et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure［J］.Journal of Fluid Mechanics，2005，537:387-413.