基于三维空间域模型的上行链路信道估计

周杰，曹志钢，菊池久和

(1.南京信息工程大学电子与信息工程学院，南京210044;2.日本国立新泻大学 电气电子工学科，新泻950-2181)

近年来，在无线通信中对MIMO(multiple-input multiple-output)系统［1-3］的研究越来越多，建立能够准确描述信道多径效应的无线信道模型，对于研究无线移动通信系统有着重要的作用。同时，移动通信领域中的信道均衡［4］、信道编码［5］以及信道调制［6］等都极大程度地依赖于无线信道的特性。早在1999年和 2002年，Ertel.R 和 Petrus.B 就分别提出了散射体空间分布圆模型和椭圆模型［7-8］。在此基础上又提出了Mahmoud.S和Jaafar.I的散射体双曲线分布模型散射体空心圆环分布模型［9-10］以及Jiang.L［11-12］的基于瑞利分布和指数分布圆模型等。但是以上模型仍然存在一定的估计错误，都没考虑过俯仰角对信道参数估计的影响。文献［13-14］给出了测量结果，表明在俯仰角大于10°情况下，波达信号中大约包含了65%［13］的总能量，当俯仰角在0°～10°时，波达信号中包含了 90%［14］的总能量。在文献［15］中 K.B.Baltzis提出一种三维空间信道模型，基站的位置离地面具有一定的高度，而散射体分布空间则是一个二维平面空间的圆形区域。例外，S.J.Nawaz也提出一种在基站有指向性天线的三维空间信道模型［16］，引入了主瓣宽度为2α的指向性天线。

但是，以上这些三维空间信道模型都是假设在整个散射体覆盖下服从均匀分布，没有考虑到移动台周围可能出现极端特殊情况。比如在许多体育运动比赛现场观众数量众多时，很容易造成电子设备(移动台)周围散射体数量稀少，甚至于为零。这就需要一种改进的三维信道模型来准确地描述波达信号的传播特点。可以发现，在各种体育比赛中此特殊通信环境是广泛存在的。本文针对此特定的移动通信环境，建立一种三维空间域统计信道模型，并且估计出此空间信道的重要时空信道参数。

1 三维空间统计信道模型

1.1 三维空间信道模型

如图1所示，本文建立一种三维空间统计信道模型。假设在信道模型中，所有散射体分布在一个空心半椭圆球体Ⅰ空间内，椭圆球体长轴为a1，短轴为b1，而空心椭圆球体长轴为a2，短轴为b2。基站离地面的垂直高度为H，基站到移动台的水平距离为D。图1显示任意散射点SP反射产生的来波信号方位角和俯仰角分别为φm和βm，散射体点到移动台的距离为rm。

图1 三维空间统计信道模型Fig.1 3D spatial statistical channel model

如图1，散射体分布空间体积为

式中:V1和V2分别为大、小半椭圆球体的体积。

1.2 上行链路AOA概率密度分布

假设散射体在三维空间信道模型内是均匀分布的，则散射体分布函数为

式中:Ⅰ是空心椭圆球体的散射体分布空间，V是散射体分布空间体积。

通过雅可比式将坐标(xm，ym，zm)转换为(rm，βm，φm)，计算得到到达角度(angle of arrival，AOA)联合分布函数:

式(1)对rm进行积分，可以得到p( βm，φm)联合概率密度函数:

其中，

对式(2)直接积分βm，计算得到方位角的边缘概率密度函数:

俯仰角的边缘密度函数可以通过同样的方法得到

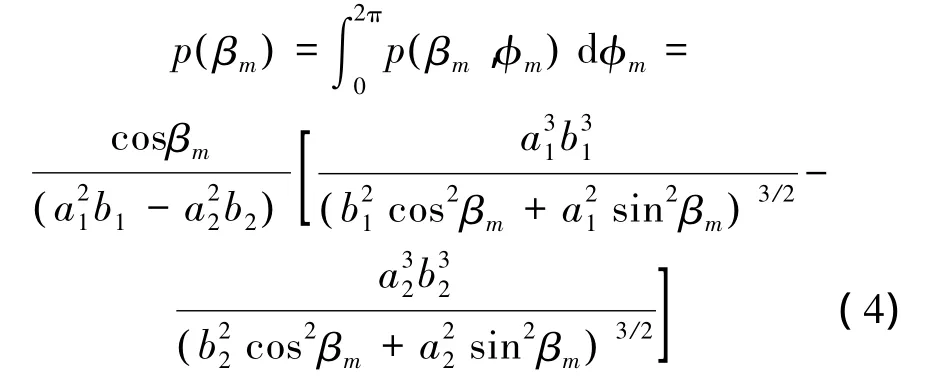
从式(3)和(4)中可以发现，p( φm)和p( βm)之间是相互独立的，即

2 上行链路TOA概率密度分布

对任何散射体反射的信号，从基站到移动台存在传播路径，其到达时延τ为

式中:c为光速。基站与移动台之间的最短距离为直达视距DLOS，则信号的到达时延最小值τmin为

其到达时延的最大值τmax为

通过三角函数计算可以到rb关于的表达式:

利用雅可比转换，同样推导出上行链路的AOA/TOA联合概率密度函数:

对式(7)进行βm积分，计算得到移动台的方位角到达时间(time of arrival，TOA)联合分布函数:

其中，

3 多普勒频移概率密度分布

在三维空间信道模型中，移动台的移动特性会使信号产生多普勒频移(Doppler shift，DS)。因此，多普勒频移与传播路径中角度的关系为

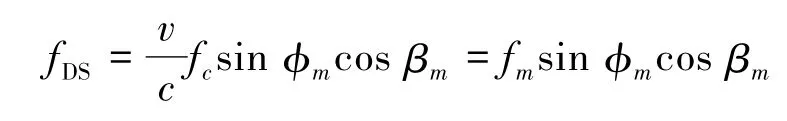
式中:fc为信号的载波频率，fm=vfc/c是最大多普勒频移。定义γ≡fDS/fm，则有

为求解多普勒频移的概率密度函数，可采用求解多普勒频移的累积分布函数(cumulative density functions，CDFs):

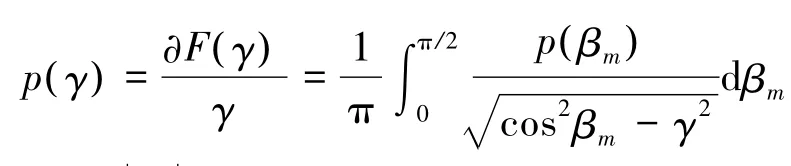
将式(4)代入式(9)，并且令x=sin βm，ε1=a1/b1和 ε2=a2/b2，则有

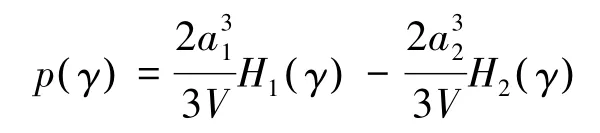
其中，

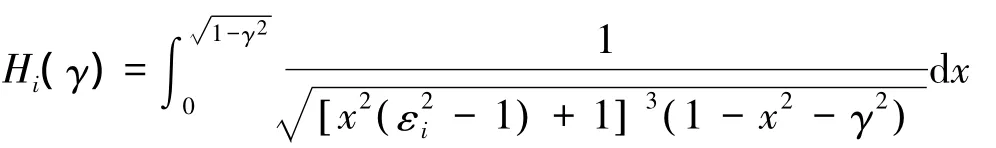
利用文献［17］，计算得到多普勒频移概率密度函数的表达式:

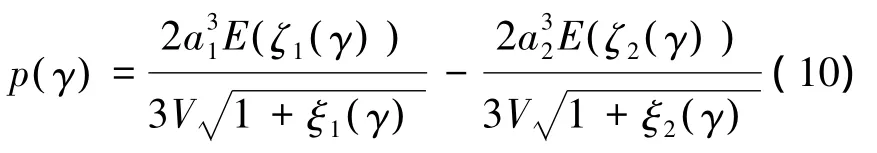
其中，

式中:V是散射体分布空间，E(·)是第二类完全椭圆积分，定义为

4 仿真结果分析

4.1 AOA 结果分析

图2给出了参数a1/b1对上行链路俯仰角边缘密度函数的影响。从图中可以看出，随着a1/b1不断增大，俯仰角的概率密度分布主要集中在βm=0°处，而在大角度处βm≥50°其概率分布非常小。这是因为随着a1/b1不断增大，即椭圆体短轴的不断变小，散射体在俯仰角小角度的数量比在大角度的数量要多，从而导致其信号的反射概率比较大。特别地，当a1/b1=1时，俯仰角边缘密度函数曲线正好是一条余弦函数曲线。图3显示了在空心椭圆球体取不同形状下，俯仰角边缘密度分布的变化规律。当a2＜b2，与图2相比较，随着短轴的减小，图3的密度函数曲线变化趋势波动比较小，但还是一条单调变化的曲线。而当a2＞b2，此时的曲线出现了极大值，极大值出现的地方随着长轴a2的增大而向俯仰角大角度靠拢。特别地，当a2增大到100 m极限长度时，其概率密度函数分布在βm=0°的取值为零，其最大概率在βm=40°左右。与Janaswamy模型［18］比较可以发现，只要a1/b1=a2/b2的比值与Janaswamy模型是相同，其仿真结果是一致的。这说明不管移动台周围空心散射体空间如何变化，其参数a1/b1对上行链路俯仰角边缘密度函数的影响主要取决于外围散射体空间的大小。

图2 参数a1/b1对俯仰角边缘密度函数的影响(D=500 m，H=100 m，a1=100 m，a1/b1=a2/b2)Fig.2 The influence of the parameter a1/b1on the EA marginal density function(D=500 m，H=100 m，a1=100 m，a1/b1=a2/b2)

图3 不同空心形状对俯仰角边缘密度函数的影响(D=500m，H=100m，a1=b1=100m)Fig.3 The influence of the different hollow shape on EA marginal density function(D=500m，H=100m，a1=b1=100m)

4.2 TOA 结果分析

图4为上行链路方位角的TOA联合概率密度。从图中可以发现，方位角的TOA最大概率主要集中在最小时延τmin和方位角φm=0°的区域。作为对比图，同时给出了Janaswamy模型［18］的TOA估计结果。图4可以看出，随着空心率(a2/a1的比值)的不断变大，TOA联合密度函数分布主要集中在大角度和长时延处。当a2→a1时，三维空间模型趋近于三维圆环模型，此时TOA联合分布函数呈现“人型”分布。如果假设a2=b2→0、H→0和b1→0，本文提出的模型就转化为Ertel.R圆模型［7］，两者的分析结果是一致的。

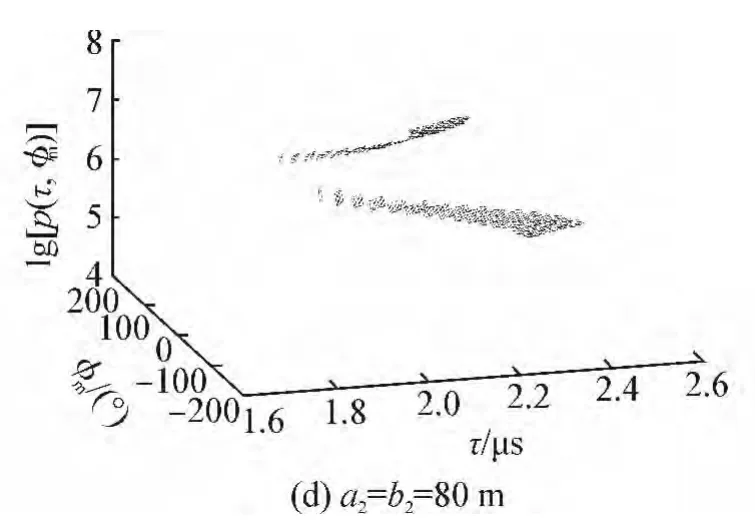
图4 上行链路方位角的TOA联合概率密度分布(D=500 m，H=100 m，a1=b1=100 m)Fig.4 The TOA joint probability density distribution of the uplink AA(D=500 m，H=100 m，a1=b1=100 m)

图5为俯仰角的时延特性TOA联合概率密度分布。移动台MS接收信号表现集中在全方位和短时延。随着空心率的增加，受远处散射体的影响，移动台所接收信号经历角度到达和时延也不断增大。但是不管空心率怎么变化，TOA联合概率密度峰值始终在(τp，φmp)点达到峰值，其中 τp=τ+min和φm=0+。这是因为信号在直达视距LOS上的散射体反射概率是最大的，数值结果符合信道定性分析。

图5 上行链路俯仰角的TOA联合概率密度分布(D=500 m，H=100 m，a1=b1=100 mFig.5 The TOA joint probability density distribution of the uplink EA(D=500 m，H=100 m，a1=b1=100 m)

4.3 DS 结果分析

图6为参数a1/b1(ε1)对多普勒频移的概率密度函数的影响。图7显示了不同形状的三维散射体空间对多普勒频移概率密度的影响。在图6中，随着ε1逐渐增大，多普勒频移的概率密度值|γ|=1不断变大。从图7中可以发现，当b2＜a2=50 m时，其图形是倒U型，多普勒频移概率密度的最大值在|γ|=0处。而当b2＞a2=50 m时，最大值在|γ|=1处。这是因为随着移动台周围空心散射体区域的逐渐变大，俯仰角的密度函数逐渐变小，从而导致多普勒频移密度函数的改变。

对于特殊情况:

1)当ε1→∞，即b1=0时，三维空间模型就变成了经典Clarke二维模型，俯仰角的密度函数可以看作p(βm)=δ(βm)，其中 δ(·)是狄拉克 δ函数。则经典Clarke二维模型的多普勒频移概率密度函数为

2)当 ε1= ε2=1，即a1/b1=a2/b2时，由式(10)可以看出p(γ)=1/2(图6所示)。也就是说只要中间空心散射体区域的比例不变时，多普勒频移的概率密度函数是不变的，这是由于椭圆体模型的特殊性所决定的。

图6 参数a1/b1对多普勒频移的概率密度函数的影响(D=500 m，H=100 m，a1=100 m，a1/b1=a2/b2)Fig.6 The influence of the parameter a1/b1on the DS probability density function(D=500 m，H=100 m，a1=100 m，a1/b1=a2/b2)

图7 不同空心形状对多普勒频移概率密度函数的影响(D=500 m，H=100 m，a1=b1=100 m)Fig.7 The influence of the different hollow shape on DS probability density function(D=500 m，H=100 m，a1=b1=100 m)

5 结束语

针对某些特殊的移动通信环境，比如移动台周面散射体为零，本文建立了新的三维空间统计信道模型。与二维空间模型比较，本文在上行链路中分别推导出了方位角和俯仰角的AOA边缘密度函数，拓展了波达信号在垂直面内的参数估计。与三维信道模型相比较，本文给出了波达信号TOA联合密度函数的解析表达式，更好地阐明了方位角和俯仰角的TOA联合分布特点。通过移动台周围空心形状的极限变形，本模型能转换成三维Janaswamy模型［18］。而当加入指向性天线时，本模型就能转换为S.J.Nawaz模型［16］，说明本模型适用于多种移动通信环境，为三维空间中信道统计特征的研究提供有力的研究工具。

［1］CHUNG J M，KIM J，HAN D.Multihop hybrid virtual MIMO scheme for wireless sensor networks［J］.IEEE Transactions on Vehicular Technology，2012，61(9):4069-4078.

［2］NISHIMORI K，HONMA N，MURAKAMI T，et al.Effectiveness of relay MIMO transmission by measured outdoor channel state information［J］.IEEE Transactions on Antennas and Propagation，2012，60(2):615-623.

［3］ZHANG Lu，LI Yongzhao，CIMINI L J.Statistical performance analysis for MIMO beam forming and STBC when co-channel interferers use arbitrary MIMO models［J］.IEEE Transactions on Communications，2012，60(10):2926-2937.

［4］CHEN B S，YANG Changyi，LIAO Weiji.Robust fast timevarying multipath fading channel estimation and equalization for MIMO-OFDM systems via a fuzzy method［J］.IEEE Transactions on Vehicular Technology，2012，61(4):1599-1609.

［5］BURSALIOGLU O Y，CAIRE G，DIVSALAR D.Joint source-channel coding for deep-space image transmission using rateless codes［J］.IEEE Transactions on Communications，2013，61(8):3448-3461.

［6］SABRY M M，SRIDHAR A，MENG Jie，et al.An energyefficient liquid cooling design technique for 3-D MPSoCs via channel width modulation［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2013，32(4):524-537.

［7］ERTEL R B，REED J H.Angle and time of arrival statistics for circular and elliptical scattering model［J］.IEEE Journal on Selected Areas in Communications，1999，17(11):1829-1840.

［8］PETRUS P，REED J H，RAPPAPORT T S.Geometricalbased statistical macrocell channel model for mobile environments［J］.IEEE Transactions on Communications，2002，50(3):495-502.

［9］MAHMOUD S S，AL-QAHTANI F S，HUSSAIN Z M，et al.Spatial and temporal statistics for the geometrical-based hyperbolic macrocell channel model［J］.Digital Signal Processing，2008，18(2):151-167.

［10］JAAFAR I，BOUJEMAA H，SIALA M.Angle and time of arrival statistics for hollow-disc and elliptical scattering models［C］//Proceedings of the 2nd International Conference on Signals， Circuits and Systems.Monastir，2008:1-4.

［11］JIANG Lei，TAN S Y.Geometrically based power azimuth spectrum models for mobile communication systems［J］.Microwave and Optical Technology Letters，2007，49(9):2093-2097.

［12］JIANG Lei，TAN S Y.Geometrically based statistical channel models for outdoor and indoor propagation environments［J］.IEEE Transactions on Vehicular Technology，2007，56(6):3587-3593.

［13］KUCHAR A，RROSSI J P，BONEK E.Directional macrocell channel characterization from urban measurements［J］.IEEE Transactions on Antennas and Propagations，2000，48(2):137-146.

［14］FULH J，ROSSI J P，BONEK E.High-resolution 3-D direction-of-arrival determination for urban mobile radio［J］.IEEE Transactions on Antennas and Propagations，1997，45(4):672-682.

［15］BALTZIS K B，SAHALOS J N.A simple 3-D geometric channel model for macrocell mobile communications［J］.Wireless Personal Communications，2009，51(2):329-347.

［16］NAWAZ S J，QURESHI B H，KHAN N M.A generalized 3-D scattering model for a macrocell environment with a directional antenna at the BS［J］.IEEE Transactions on Vehicular Technology，2010，59(7):3193-3204.

［17］JEFFREY A，ZWILLINGER D.Tables of integrals，series，and products［M］.7th ed.New York:Academic Press，2000:1-10.

［18］JANASWAMY R.Angle of arrival statistics for a 3-D spheroid model［J］.IEEE Transactions on Vehicular Technology，2002，51(5):1242-1247.