柔性机体下船舶柴油机主轴承TEHD润滑分析

魏立队，段树林，魏海军

(1.上海海事大学商船学院，上海201306;2.大连海事大学 轮机工程学院，辽宁 大连116026)

船用二冲程十字头式主柴油机的主轴承是典型的动载径向滑动轴承，其工作的优劣，将直接影响到轴系，甚至整个柴油机和船舶的安全性、可靠性和经济性，因此对于主轴承的研究具有非常重要的意义。近年来，在热流体动力润滑THD(thermo-hydrodynamic)、弹性流体动力润滑 EHD(elasto-hydrodynamic)、计入轴系不对中和轴承表面形貌影响的混合润滑研究的基础上，随着润滑理论的发展和计算能力的提升，热弹性流体动力混合润滑TEHD(thermo-elasto-hydrodynamic)的研究逐渐增多，但轴承支撑多限于单轴承座［1-6］，与整机体支撑的实际情况差异较大，无法考虑在工作过程中各轴承之间的相互影响。但是，若基于柔性整机体并计入对润滑影响较大的温度因素(即TEHD润滑)，计算成本将非常高昂。在此背景下，本文运用CMS(component mode synthesis)模态综合法，通过对机体和曲轴的缩减，运用质量守恒边界条件的广义Reynolds方程和Greenwood/Tripp理论，建立了柔性整机体模型下的柴油机主轴承的热弹性流体动力混合润滑模型，通过与单轴承座模型的TEHD润滑和柔性整机体模型下不计入温度影响的EHD润滑对比，表明该模型建模方法具有较高应用价值。

1 润滑计算基本理论和控制方程

1.1 基于CMS法缩减的机体和曲轴的运动方程

鉴于柔性机体和曲轴自由度数量的庞大，运动方程的求解效率非常低下，因此必须对结构自由度数量缩减。

根据 Craig-Bampton模态综合法［7］，机体物理坐标与模态坐标间转换关系如下:

机体的运动方程为

式(1)代入式(2)，得到缩减后机体运动方程:

因计入了曲轴大范围刚体运动旋转惯性的影响，曲轴的运动方程和转换方程分别为［8］

式(5)代入式(4)则得到曲轴缩减运动方程:

式中:x为物理坐标，下角标r、i分别为保留自由度(包括所有载荷点和边界点自由度)和内部自由度，θ为曲轴旋转角坐标，α为主模态坐标(亦称模态参与因子)，q为广义位移矢量。上角标b、c分别代表机体和曲轴，下角标θ、f分别代表刚体旋转和柔性变形。M、C、K分别代表质量矩阵、阻尼矩阵和刚度矩阵，上横线代表缩减后物理量。T为静态缩减矩阵。φ、Φ分别为机体和曲轴的坐标转换矩阵。力F中包括了机体外载荷矢量、油膜力和微凸峰接触力包括离心力和科氏力为曲轴广义外载荷矢量，包括油膜力和微凸峰接触力。

1.2 广义Reynolds方程

对于主轴承，基于JFO质量守恒边界条件和广义Reynolds方程，建立含滑油填充率的扩展Reynolds方程［9］。

其中，

其中，在全油膜润滑区:

在穴蚀区域:

式中:x、y、z为轴承展开周向、径向、轴向坐标;y'为仅用于积分的径向间隙坐标;=y/h;θ-为滑油填充率;p、pc分别为油膜压力和空穴压力;h为间隙厚度;η、ρ分别为滑油动力粘度和密度;η'=η/η*，η*为参考温度及压强下的动力粘度;uJ、uS分别为轴颈和轴瓦的周向速度;t为时间。求解采用有限体积法，边界条件参照文献［10］。

1.3 能量方程

忽略体积力和热辐射影响，滑油能量方程［11］:

式中:μ0为边界摩擦系数，κ为流体导热系数，cp为滑油比热容。

1.4 轴瓦热传导方程

式(16)边界条件参见文献［12］，r为径向坐标。

1.5 轴颈温度方程

因轴颈表面周向温度变化很小，视其为等温体，其热流量满足:

式中:TS为轴颈温度，λf为滑油热导率。

1.6 微凸峰载荷

根据Greenwood和 Tripp理论［12］，表面微凸峰接触压力计算公式为

其中，

当h/σs＜4，即在微凸峰接触区时，

当h/σs≥4，即在完全液动润滑区时，

式中:υ1、υ2分别为轴颈、轴瓦泊松比，E*为当量弹性模量，β为微凸峰曲率半径，σ1、σ2分别为轴颈和轴瓦表面的粗糙度，σs为表面综合粗糙度。

1.7 主轴承的摩擦力与摩擦功耗

在混合润滑状态下，摩擦力由流体摩擦力和峰元摩擦力2项组成:

式中:τH为流体剪应力，τA为峰元剪应力，Pf为摩擦功耗。

1.8 滑油端泄流量

滑油端泄流量为

2 数值计算方法

由于方程系统的高度非线性，机体和曲轴的运动方程求解均采用时域隐式直接积分的向后微分法BDF(backward differentiation formulae)。Reynolds方程运用有限体积法求解、固体热传导方程和能量方程均使用有限差分法进行离散求解，机体和轴颈弹性变形采用有限元方法计算。求解过程中，轴颈、轴瓦热弹变形与油膜压力和接触压力产生的弹性变形相互影响，计算工作量很大，故方程系统计算运用时间步长可变的N-R迭代法求解，在每一时间步下，必须满足轴颈、轴瓦、油膜间的热平衡和曲轴与机体间的动平衡关系。

3 计算结果与分析

图1为大型低速十字头式二冲程MAN 6S50MC-C型6缸船用柴油机单轴承座和曲轴模型、机体和曲轴有限元模型。机体缩减时，轴承表面所有节点和机座上的固定约束节点均保留。图2为各缸气体压力曲线，根据气体压力、活塞组件和连杆的惯性力计算载荷，施加于曲轴各曲柄销上，在曲轴的飞轮端施加计算所得的平均反向扭矩。

轴瓦宽192 mm，轴瓦半径300 mm，轴瓦/轴颈间隙0.3 mm，轴瓦/轴颈弹性模量分别为150/210 GPa，泊松比均为 0.3，轴瓦/轴颈粗糙度分别为 4/0.5 μm，轴瓦/轴颈膨胀系数分别为 1.67×10-5/1.18×10-5K-1，导热系数均为50 W·m-1·K-1，润滑油为SAE30W，供油温度、压力分别为 45°C、0.4 MPa，轴颈转速 127 r/min。

图1 轴承座、机体和曲轴模型Fig.1 Model of bearing housing，engine block and crankshaft

图2 各缸示功图(点火顺序:1-5-3-4-2-6)Fig.2 Indicator diagram of cylinders(firing order:1-5-3-4-2-6)

3.1 单轴承座与柔性整机体模型下轴承特性对比

图3表明，与单轴承座相比，在整机体模型下，趋势虽较一致，但最大油膜压力pmax1和最大接触压力整体偏小较多，整周期内的最小油膜厚度却增加。最大油膜温度降低也非常明显，端泄流量趋势差异明显，4#、6#轴承在整机体模型的平均流量分别为7.39×10-2、7.72 ×10-2m3/min，而在单轴承座下为7.44 ×10-2、9.17 ×10-2m3/min，降低比例较高。混合润滑中的微凸峰接触百分比，整体趋势一致，但局部差异较大，4#、6#单轴承座/整机体模型下接触分别为 1.61%/2.27%、5.39%/4.08%，一增一降，而摩擦功耗却均降低(见表1)，表明整机体的载荷协调作用。而表征穴蚀发生几率的最小油膜填充比，2模型中最易发生穴蚀的时刻并不完全一致，整体而言，单轴承座模型下更易发生穴蚀。

对于4#轴承的最大接触力发生位置(见图4)，单轴承座模型在上下轴瓦均有发生，而整机体模型则主要集中在下瓦，轴向二者虽然发生位置不完全一致，但两端面发生接触的时段均较为平均。6#轴承中，2模型的发生位置较为一致。因此，对于4#轴承而言，则必须重点关注下瓦的磨损。

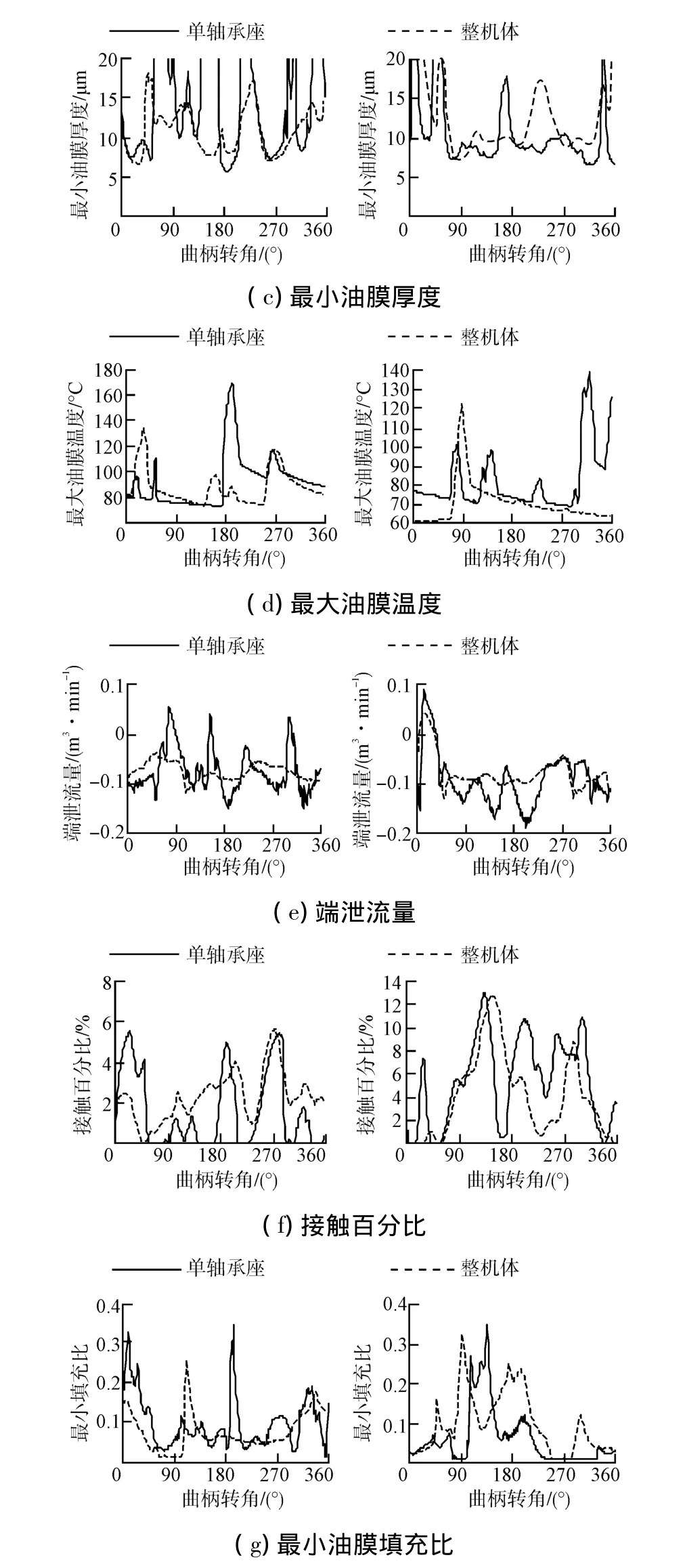
图3 单轴承座与整机体模型下轴承特性对比Fig.3 Comparison of bearing characteristics in the single bearing housing model and the whole engine block model

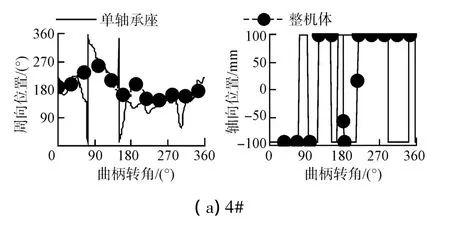
图4 最大接触力时发生位置Fig.4 Position at the maximum film temperature moment

表1中各轴承计算数据表明，在整机体模型下，除5#轴承外，最大接触压力pmax2、最高油膜温度Tmax、平均摩擦功耗P降低，而最小油膜厚度hmin增加，整体润滑状况较单轴承座良好，同时从图3、图4中的曲线表明，整机体模型中变化较为平缓，而单轴承模型中突变较多，由此表明:整机体模型能够协调各轴承间的相互影响，对载荷有“柔化”均衡作用，整机体模型更加贴近实际。相反，说明单轴承座模型计算比较保守。

表1 整周期内各主轴承计算数据(不同支撑模型)Table 1 Calculating data of bearings during cycles(under different supporting models)

3.2 整机体模型中轴承TEHD与EHD润滑特性对比

图5和表2表明，在整机体模型下，计入温度影响的TEHD与不计入温度影响的EHD相比，除最大接触压力增加明显外，最大油膜压力增加也较大，最小油膜厚度却明显降低。端泄流量趋势变化较为一致，端泄流量增加，周期内的接触比增加非常明显，故多数轴承的摩擦功耗也增加。周期内接近零油膜填充比时段明显增多，无疑将大大增加穴蚀发生的机会。

图5 计入与不计入温度影响时轴承特性对比Fig.5 Comparison of bearing characteristics with or without temperature effect on film

图6中，不计入温度影响的EHD模型，4#轴承最大接触力位置上瓦也有发生，且轴向集中于中间区域，而TEHD模型下主要在下瓦、两端面;6#轴承相似，EHD中上下瓦均有发生，且单端面发生，而TEHD模型中，发生在下瓦和2个端面。显然，均是温度增加导致油膜粘度降低，承载力降低，流动性加强和粗糙表面受热变形所致。因此，不计入温度的影响，不可能对各轴承润滑进行准确的预测。

表2 整周期内各主轴承计算数据(相同整机体模型下)Table 2 Calculating data of bearings during cycles(under the model of the whole engine block)

图6 最大接触压力时发生位置Fig.6 Position at the maximum asperity contact moment

3.3 3模型计算时间对比

图7为单轴承座S-TEHD、整机体W-EHD和整机体W-TEHD 3种模型下的计算时间对比。显然，相对于不计入温度影响的整机体模型，计入温度影响的单轴承座模型计算成本更大。计入温度影响，基于CMS缩减的柔性整机机体模型较单轴承座模型计算时间增加并不多。因此，从计算成本考虑整机体模型下TEHD润滑计算也是可接受的。

图7 3模型计算时间对比Fig.7 Comparison of calculating time of three models

4 结论

1)基于CMS模态综合法建立了柔性整机体模型下的船舶柴油机主轴承的热弹性流体动力混合润滑TEHD计算模型。

2)单轴承座与整机体模型下对比表明，单轴承座模型的计算偏于保守，且各参数指标突变较多。相反，整机体模型能够计入工作过程中各轴承间的相互影响，使各参数变化平缓，更加接近实际。

3)柔性整机体下TEHD模型和EHD模型对比则发现:不计入温度影响的弹性流体动力润滑不能够全面、较为准确的反映轴承的润滑形貌。

4)从单轴承座模型TEHD、柔性整机体模型TEHD和柔性整机体模型下EHD 3种模型计算时间对比看，温度对润滑的影响较柔性整机体模型而言计算成本更高。与单轴承座相比，从计算成本考虑，基于柔性整机体的TEHD计算是可接受的。

［1］OKAMOTO Y.Numerical analysis of lubrication in a journal bearing by a thermo-elasto-hydrodynamic lubrication(TEHL)model［J］.International Journal of Engine Research，2005，6(2):95-105.

［2］童宝宏，桂长林，孙军，等.计入热变形影响的内燃机主轴承热流体动力润滑分析［J］.机械工程学报，2007，43(6):180-185.TONG Baohong，GUI Changlin，SUN Jun，et al.Thermohydrodynamic lubrication analysis of internal combustion engine’s main bearing considering thermal deformation effects［J］.Chinese Journal of Mechanical Engineering，2007，43(6):180-185.

［3］张俊岩，王晓力.高功率密度柴油机主轴承混合润滑特性［J］.内燃机学报，2011，29(1):90-95.ZHANG Junyan，WANG Xiaoli.Performance of main bearing in mixed lubrication of high power-density diesel engine［J］.Transactions of CSICE，2011，29(1):90-95.

［4］何涛，邹德全，卢熙群，等.考虑轴挠曲的船舶艉轴承混合润滑分析［J］.哈尔滨工程大学学报，2013，34(1):104-109.HE Tao，ZOU Dequan，LU Xiqun，et al.Mixed lubrication analysis of a ship stern bearing considering bending of shaft［J］.Journal of Harbin Engineering University，2013，34(1):104-109.

［5］HE Zhenpeng，ZHANG Junhong，XIE Weisong，et al.Misalignment analysis of journal bearing influenced by asymmetric deflection，based on a simple stepped shaft model［J］.Journal of Zhejiang University-Science A，2012，13(9):647-664.

［6］LIN Qinyin，WEI Zhengying，WANG Ning，et al.Analysis on the lubrication performances of journal bearing system using computational fluid dynamics and fluid-structure interaction considering thermal influence and cavitation［J］.Tribology International，2013，64:8-15.

［7］BAMPTON M C C，CRAIG R R，Jr.Coupling of substructures for dynamic analyses［J］.AIAA Journal，1968，6(7):1313-1319.

［8］HU K，VLAHOPOULOS N，MOURELATOS Z P.A finite element formulation for the coupling rigid and flexible body dynamics of rotating beams［J］.Journal of Sound and Vibration，2002，253(3):603-630.

［9］KRASSER J.Thermo-elasto-hydrodyanmic analysis of dynamically loaded journal bearings［D］.Graz:Technology University of Graz，1996:93-98.

［10］SHARMA S C，KUMAR V，JAIN S C，et al.Study of hole-entry hybrid journal bearing system considering combined influence of thermal and elastic effects［J］.Tribology International，2003，36(12):903-920.

［11］BUKOVNIK S，OFFNER G，AIKA V，et al.Thermoelasto-hydrodynamic lubrication model for journal bearing including shear rate-dependent viscosity［J］.Lubrication Science，2007，19(4):231-245.

［12］GREENWOOD J A，TRIPP J H.The contact of two nominally flat rough surfaces［J］.Proceedings of the Institution of Mechanical Engineers，1970，185(1):625-633.