交叉相遇局面让路船自动避碰行动方案
贺益雄,黄立文,牟军敏,熊勇
(1.武汉理工大学航运学院,湖北武汉,430063;2.武汉理工大学内河航运技术湖北省重点实验室,湖北 武汉,430063)
以往自动避碰研究中,行动方案多以来船方位、航速等确定[1-2]。郑中义[1]对局面划分和避碰行动进行了研究,建立了碰撞危险度模型;李丽娜等[3]基于船舶拟人智能避碰决策系统进行了相关研究。近年来,国内外学者基于专家系统原理、模糊数学、神经网络技术、多Agent技术等方法、导弹制导、机器人避碰原理等展开了广泛研究[4]。以往研究存在以下不足:1)对来船航向、两船相对方位等因素考虑不足;2)未考虑会遇不同阶段。阶段不同应采取行动可能完全不同;3)对操纵性能、船型尺度等因素考虑不足;4)不完全符合《1972国际海上避碰规则》(简称《规则》)和海员通常做法[4]。目前相关成果离应用还有较大差距。
远洋船舶大部分时间航行于船舶密度较小、天气较好的开阔水域。如能在这种环境中率先实现自动避碰,对减轻船员劳动强度、降低人为因素对安全的影响和降低成本具有重大意义。开阔水域中同时避让两艘或以上船舶的概率很低。即使需要,也是先行避让最危险船舶,再避让其他船舶。两船环境下自动避碰也是多船环境下自动避碰实现的前提和基础。因此良好天气、开阔水域中两船相遇时,确定目标船危险程度、会遇局面阶段和生成自动避碰方案是自动避碰最终实现的前提和基础。根据《规则》,两船在海上以交叉相遇态势相遇直至发生碰撞可分为多个阶段[5],不同阶段让路船应采取的避碰行动可能完全不同。航海实践中驾驶员按《规则》、海员通常做法和本人知识、技能、经验等,确定避碰行动方案并执行。人是智能的,可智能地判断局面、阶段并决定方案。而自动避碰须依赖计算机完成,只有对会遇阶段进行准确划分,计算机才能判断并生成避碰方案。各阶段必须严格定义,使机器判断成为可能。研究从《规则》和海员通常做法出发,以MMG模型和船舶领域理论为基础,根据碰撞危险、紧迫局面和紧迫危险的公认理解或定义,研究其定量模型,结合碰撞危险度模型,对整个交叉相遇局面进行阶段划分。在阶段划分基础上按《规则》、海员通常做法和新研究发现的最有效避碰行动方向判定模型提出交叉相遇局面让路船各个阶段自动避碰方案。
1 自动避碰行动方案建模
1.1 假设与定义
假设 环境为天气良好的无流开阔水域;鉴于定速航行的大型船舶采取变速行动来避让他船基本是不可能的,自动避碰方案中不考虑变速;不考虑协调避让;来船船位、航向、航速已知;两船构成《规则》中所定义本船为让路船的交叉相遇局面。
定义1 本船/来船:指交叉相遇局面中让路船/直航船;来船方位位于本船桅灯光弧之内并构成最终碰撞危险,但不构成对遇或追越局面。
定义2 船舶领域和动界:采用文献[6-7]定义;
定义3 碰撞危险,是指满足以下条件局面:1)保向保速,来船最终会进入本船船舶领域;2)来船进入本船桅灯可见范围;3)TCS≤20 min,紧迫局面时间(time to close situation,TCS):当前到 PCSF的时间。最终碰撞危险(collision risk at last,CRAL)表示不论当前有没有碰撞危险,两船如保向保速,将最终出现碰撞危险。碰撞危险形成点(point collision risk formed,PCRF)表示从该时间点开始形成碰撞危险。
定义4 紧迫局面:该局面下,本船右满舵转向,来船亦将进入本船船舶领域;PCSF为一时间或位置点,此时本船右满舵转向,来船将与本船船舶领域边界相切。
定义5 紧迫危险:该局面下本船右满舵转向,两船亦将碰撞。碰撞含义定为两船重心距离小于两船船长之和一半。PIDF为本船满舵向右转向,两船不碰撞的最后时间点;紧迫危险时间(time to immediate danger,TID):当前到PIDF时间。
定义6 碰撞危险度(CRI):指微观危险度[1,12],两船位置、运动等关系所确定的碰撞危险度量。
定义7 空间碰撞危险度(SCRI)/时间碰撞危险度(TCRI):借鉴文献[1,12]定义确定为:SCRI是会遇中船舶保向保速发生碰撞的可能性度量;TCRI是指会遇中一船按照《规则》和海员通常做法采取措施避免紧迫局面在时间上的紧迫性度量。
1.2 船舶会遇局面分析
根据两船在海上相遇直至发生碰撞可分为以下4 个阶段[5]:
1)PCRF之前,碰撞危险未形成的自由行动阶段;2)PCRF和PCSF之间,碰撞危险形成但紧迫局面未形成阶段;3)PCSF和PIDF之间紧迫局面形成但紧迫危险未形成阶段;4)PIDF之后,紧迫危险至碰撞发生阶段。
PCRF之前让路船可自由行动,因此自动避碰方案中应选择最有效的避让方式;PCRF之后,《规则》15条要求让路船避免横越他船前方,考虑到一般船舶不会选择向左旋回一圈的避让方式,亦即要求让路船向右避让。PCSF之后,按照《规则》18条,为避免碰撞,必要时应背离规则采取行动,让路船应采取最有效的避让方式。在不考虑变速避让时,最有效的避碰方式实际上只需确定向哪舷操满舵。
2 避碰局面要素定量计算建模
2.1 坐标系
为便于计算,采用图1所示坐标系。大地固定坐标系XOY:X、Y轴和方向正向指向正东、正北和向右;随船移动坐标系xoy:y、x轴和方向正向指向船首、右舷和向右。两坐标系夹角为本船航向TC,与物标方位TB和舷角Q有

坐标转换关系:


图1 坐标系Fig.1 Coordinate system
2.2 船舶领域模型
[6-9],考虑到《规则》第 15、16条相关规定,采用偏移中心圆形船舶领域模型,参见图2。圆心为虚拟船位置,实际船位位于虚拟船位左后方。船舶领域的半径,实际船位相对于中心偏移量等参数可由船长适当选取。模拟对象为一艘7.6万吨级满载散货船,开阔水域中半径R取6倍船长,中心偏移方向199°、距离为3倍船长。

图2 采用的船舶领域Fig.2 Ship domain used
2.3 船舶运动模型
船舶避碰过程中纵摇、垂荡、横摇运动研究意义不大,只需研究静水中纵向、横向和首摇3个方向的运动。因此,本文采用MMG三自由度船舶运动模型:

式中各个符号的含义详见文献[10-11]。船位坐标计算基于上述模型和龙格-库塔方法。
2.4 避碰要素定量计算模型
2.4.1 碰撞危险
根据定义3,设不同时刻来船沿船舶领域中心方向距离船舶领域边界距离为Dis(参见图3):
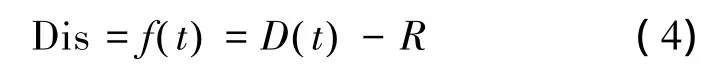

图3 函数Dis变量涵义Fig.3 The meaning of variables in function Dis
式(4)中D(t)表示t时刻船舶领域中心到来船距离。若:1)min(f(t))≥0,来船不进入本船船舶领域,则无CRAL。2)min(f(t))≤0,说明来船某时刻进入本船船舶领域,有CRAL;若满足TCS≤20 min且来船在本船桅灯可见距离内,即构成碰撞危险,否则不构成。
2.4.2 紧迫局面形成点(PCSF)计算模型
假设场景:本船保速保向至tm时刻,在tm时刻操右满舵。从当前局面开始的t时刻,他船沿船舶领域中心方向到边界距离为Dis,因此Dis是关于t和tm的二元函数。求PCSF就是求满足条件的tm=:此时操右满舵旋回,来船与本船船舶领域相切。即求

(Xt R,Yt R)由下式决定:

若t≤tm,则:

若t>tm,则:以初始条件,时间t-tm,舵角35°按方程组(3)计算。上标t代表t时刻;下标0代表本船、R代表来船;v代表速度,TC 代表航向;(x,y)、(X,Y)、(XR,YR)为本船、领域中心、来船位置。
从问题的物理意义来看,Dis=f(t,tm)具有以下性质:
1)∃t1> 0,t2> 0,tmmin(f(t,tm))单调下降;
2)若来船相距较远,不操舵来船最终进入本船船舶领域。则有:
min(f(t,0))> 0,min(f t,TCPA( ))<0
2.4.3 紧迫危险形成点定量计算
与求取紧迫局面形成点数学模型相同,将船舶领域改成以本船重心为圆心,半径为两船船长之和一半的圆形区域。
2.5 碰撞危险度(CRI)模型
2.5.1 空间碰撞危险度模型(SCRI)
参考文献[12],两船的空间碰撞危险要么存在需要采取避碰行动,要么空间碰撞危险不存在,不需要采取避碰行动。SCRI模糊集为UdT;udT为UDT隶属函数;Domaint表示t时刻船舶领域内点的集合。udT定为

2.5.2 时间碰撞危险度模型(SCRI)
设TCS变化域为Ut,TCRI模糊集为UtT,t0为定义的PCRF到PCSF时间,utT为UtT的隶属函数。则有

2.5.3 碰撞危险度(CRI)
CRI为SCRI和TCRI的合成,取论域:U=Ut×Ud即

式中:“⊕”为合成算子,采取普通实数乘法算子作为SCRI和TCRI合成CRI的合成算子。即

2.6 最有效船舶改向方向判别模型
根据《规则》和海员通常做法,在PCRF之前,让路船可自由行动,自动避碰方案中应选择最有效避让方式。碰撞危险阶段,按《规则》15条,交叉相遇局面让路船让路时应避免横越直航船前方。正常情况下,让路船不会向左旋回一圈避让,实际上是要求让路船向右转向避让。PCSF之后,按照《规则》18条,为避免碰撞,必要时应背离规则采取行动,让路船应采取最有效避让方式。以海上速度定速航行船舶,由于主机保护程序限制,降速缓慢。大型船舶惯性大,降低船速的减速效果并不明显,采取变速行动避让基本不可能。最有效避让方式实际上指的是向哪舷转向更有效。图4显示了目标船位于第一象限时,目标船相对运动线与两船航向航速关系的5种情形。其中,RVC为目标船相对速度航向;TC0为本船航向;TB00为目标船看本船真方位。
情形 1 RVC>1.5π+TC0,目标船将从本船船首通过,本船向左/右改向DCPA增加/减少,向左改向最为有效;
情形 2 RVC=1.5π+TC0,向左改向和向右改向效果基本相同;
情形 3 RVC∈(1.5π+TC0,TB00),目标船将从本船船首通过,本船向右/左改向DCPA增加/减少。向右改向是最为有效的避让方向;
情形4 RVC=TB00,目标船将与本船碰撞,向左改向和向右改向效果基本相同;
情形5 RVC<TB00,目标船将从船尾通过.本船向左/右改向DCPA增加/减少。向左改向是最为有效的避让方向。
对于情形3和情形5,同样可以分析目标船位于第四象限的5种情形,结论如图5所示。

图4 目标船相对运动线与两船航向航速关系Fig.4 The relations between relative motion lines of target ship and two ships’courses/velocities

图5 不同RVC区域的最有效改向方向示意图Fig.5 More effective direction of altering course in different RVC areas
对交叉相遇局面的让路船而言,目标船可能出现的舷角Q范围为Q∈[0,π],不同舷角范围、RVC时最有效的改向方向如表1所示。

表1 最有效改向方向Table 1 More effective direction of altering course
2.7 交叉相遇面让路船避碰行动方案
若最终无碰撞危险,无须采取行动。否则:
1)阶段1(CRI=0),碰撞危险未形成。可及早、自由地采取避让行动,按最有效改向方向模型确定改向方向。
2)阶段 2(0<CRI<1),碰撞危险已形成,未构成紧迫局面。采取向右转向可确保安全距离驶过,不应背离《规则》,程序中应规定向右转向。
3)阶段 3(CRI=1,TID>0),紧迫局面已形成,紧迫危险尚未形成,向右大幅度转向已不能安全距离驶过。按责任条款,每一船舶必要时应背离规则避免紧迫危险。应按最有效改向方向判别模型判定改向方向,幅度为操满舵,直至两船距离开始变大。
4)阶段4(CRI=1,TID≤0),紧迫危险已经形成,应采取最有助于避免碰撞的行动,此时应按最有效改向方向判别模型判定改向方向。
3 仿真计算
3.1 仿真数字船舶模型设计
以2.2节中船舶为模拟对象,使用MATLAB编程查验数字模型准确性。分别对不同转速航速和全速满舵旋回进行比较。结果表明,通过调整各系数,船舶数字模型的船速性能、旋回性能和实船可相当接近,在螺旋桨转速78~100 r/min时,速度相差小于0.3 kn;进距、旋回初径、直径等旋回圈要素相差小于50 m。
3.2 仿真流程设计
使用二分法的紧迫局面、紧迫危险形成点定量模型计算流程参见图6。以初始条件:目标船方位045°、距离 5.6 nmile、航速12 kn、航向 270°,本船初速12 kn、航向 000°。输出结果:PCSF:5 513 m/919 s后形成紧迫局面,PIDF:1 097 s。

图6 紧迫局面、紧迫危险形成点计算流程Fig.6 Computing procedure of close situation/immediate danger formed point
3.3 交叉相遇局面让路船阶段判断流程
交叉相遇局面让路船阶段判断、定量模型数值计算流程参见图7。

图7 让路船阶段判断流程Fig.7 Procedure for stage judgment of give-way ship
本文中参考文献[6]采用平移中心动界,半径2.7 nmile,中心偏移量 1.9 nmile,方位为舷角 199°。以目标船方位 045°、距离 5.656 nmile、航速 6 m/s、航向270°,本船初速6 m/s,航向000°为条件进行仿真模拟,计算输出结果:1)TCS<20 min;2)DCPA=0,TCPA=1 234.7 s;3)最终有碰撞危险;4)TRC=644 s,DRC=3 864 m来船进入动界;5)来船在动界之外,暂无碰撞危险;6)CRI=0,处于阶段1,可自由采取避让行动。
仿真结果表明,研究采用的数学模型是可靠的,二分法取小值很小(5 m)时,算法快速、可靠收敛(大循环次数一般只有5~10次);精度可以满足船舶自动避碰研究和航海实践的要求;CRI模型符合海员通常做法和驾驶员习惯思维;最有效改向方向判别模型基于来船相对运动航向、真方位和本船航向的比较可快速确定最有效转向方向。
4 结束语
研究成果可产生交叉相遇局面下让路船各个阶段避碰行动方案,结合转向模型、复航模型可生成各个时间点可能避让方案。需进一步研究本船应该采取的转向幅度和时机、复航的时机等。在局面划分的基础上发现所有可能的避碰方案,并对所有方案进行最优化选择,可最终确定符合避碰规则和海员通常做法的最优化自动避碰方案。
参考文献:
[1]郑中义.船舶自动避碰决策系统的研究[D].大连:大连海事大学,2000:7-11,31-41.ZHENG Zhongyi.Research on automatic decision-making system of vessel collision avoidance[D].Dalian:Dalian Maritime University,2000:7-11,31-41.
[2]TSOU M C,HSUEH C K.The study of ship collision avoidance route planning by ant colony algorithm[J].Journal of Marine Science and Technology,2010,18(5):746-756.
[3]李丽娜,杨神化,熊振南,等.船舶拟人智能避碰决策理论框架的研究[J].中国航海,2009,32(2):30-34.LI Lina,YANG Shenhua,XIONG Zhennan,et al.A study of theoretical framework of personifying intelligent decisionmaking for vessel collision avoidance[J].Navigation of China,2009,32(2):30-34.
[4]TAM C,BUCKNALL R,GREIG A.Review of collision avoidance and path planning methods for ships in close range encounters[J].Journal of Navigation,2010,62(3):455-476.
[5]胡甚平.船舶会遇过程中避碰阶段的划分与量化[J].中国航海,2001(2):83-87.HU Shenping.Analysis of anti-collision stages during ships’encounter[J].Navigation of China,2001(2):83-87.
[6]GOODWIN E M.A statistical study of ship domains[J].Journal of Navigation,1975,28(3):328-334.
[7]DAVIS P V,DOVE M J,STOCKEL C T.A computer simulation of marine traffic using domains and arenas[J].Journal of Navigation,1980,33(2):215-222.
[8]齐乐,郑中义,李国平.互见中基于AIS数据的船舶领域[J].大连海事大学学报,2011,37(1):48-50.QI Le,ZHENG Zhongyi,LI Gouping.AIS-data based ship domain of ships in sight of one another[J].Journal of Dalian Maritime University,2011,37(1):48-50.
[9]SZLAPCZYNSKI R.Solving multi-ship encounter situations by evolutionary sets of cooperating trajectories[J].Trans Nav,2010,4(2):185-190.
[10]朱军,庞永杰,徐玉如.规则波浪中舰船操纵运动计算[J].哈尔滨工程大学学报,2004,25(1):1-5.ZHU Jun,PANG Yongjie,XU Yuru.Maneuvering prediction of a ship in regular waves[J].Journal of Harbin Engineering University,2004,25(1):1-5.
[11]YAVIN Y,FRANGOS C.Computation of feasible control trajectories for the navigation of a ship around an obstacle in the presence of a sea current[J].Mathematical and Computer Modelling,1995,21(3):99-117.
[12]贺益雄,熊勇,黄立文,等.基于船舶领域和MMG的最晚施舵点/CRI研究[J].武汉理工大学学报:交通科学与工程版,2014,38(5):1088-1091.HE Yixiong,XIONG Yong,HUANG Liwen,et al.Studies of last steering point/CRI basis on MMG and ship domain[J].Journal of Wuhan University of Technology:Transportation Science and Engineering,2014,38(5):1088-1091.

