基于速度障碍的多船自动避碰控制方法
熊 勇, 贺益雄, 黄立文(1. 武汉理工大学 航运学院, 武汉 430063; 2. 内河航运技术湖北省重点实验室, 武汉 430063)
基于速度障碍的多船自动避碰控制方法
熊 勇1, 2, 贺益雄1, 2, 黄立文1, 2
(1. 武汉理工大学 航运学院, 武汉 430063; 2. 内河航运技术湖北省重点实验室, 武汉 430063)
传统避碰方法侧重于根据船舶实时位置设计可行的避碰路径,较少考虑结合船舶动力学和船舶运动控制来设计一个完整的自动避碰系统。对此,提出一种实用、基于相对速度方向的自动避碰方法。该方法同时考虑避碰路径规划和本船运动控制,主要包括3个部分:首先,基于运动方程计算本船和目标船的基本运动与位置参数;其次,利用速度障碍方法计算本船实时的可行避碰方向;最后,实现控制变量的变换和控制算法设计。该方法是一个灵活、容易实现的多船避碰控制算法,模拟结果显示其具有较好的效果,并给出了进一步研究的建议。
水路运输; 自动避碰; 船舶运动数学模型; 速度障碍; PID控制
当在水面上航行的船舶不断增多时,船舶碰撞的危险性就会逐渐增加。相关学者[1-4]从避碰计算和避碰方法设计的角度对船舶避碰问题进行了详细研究, 主要基于船舶的位置来设计可行的避碰方案,结果主要集中在船舶避碰路径规划和碰撞危险度评估上。这些研究隐含的假定条件是本船和目标船在碰撞发生前后一个较短的时间段内均为匀速直线运动,以此为基础来设计基于位置的避碰方案,较少考虑船舶的动力学特性。该类方法传统上称为“几何避碰方法”,是航海避碰实践的总结和提升,具有较好的实用性,主要依据船舶的位置信息和几何计算来做出避碰决策。在最近的10 a中,一些现代方法被逐渐引入到求解该问题的框架中。例如:遗传算法被用于搜寻最优避碰路径[5-7],模糊专家系统被用于构建船舶碰撞的风险评估模型[8-10]。总的来说,现有方法主要用于避碰路径规划,最终避碰是否成功还依赖于船长的操船经验和水平,其主要不足在于较少考虑在一个动态、持续变化、不确定的来船环境中,船舶如何自动、持续地完成避碰并恢复到原来的航向上。 此外,现有方法较少考虑船舶动力学,即使计算出了可行的避碰路径,也无法确认船舶是否能被控制并按设定的避碰路径行驶,因此对于自动导航而言,仅是完成了一部分功能,缺乏将避碰和船舶运动控制联接起来的完整的系统设计。基于上述考虑,从船舶自动航行的角度出发,设计一种在船舶运动方程的基础上,通过计算和控制速度而不是位置,能连续控制船舶避开障碍物并保持航向的算法。
速度障碍的概念和方法是由FIORINI等[11]首先提出的,主要指目标物和障碍物在保持当前运动状态的情况下,所有可能导致目标物与障碍物发生碰撞的速度集合。这里从速度障碍的角度考虑,提出一种实用的多船避碰控制方法,其核心思想如下。
1) 根据实时的本船速度和所有目标船速度计算本船与所有目标船的相对速度。
2) 计算可行的本船相对速度方向,使得本船的相对速度方向不指向任何目标船。
3) 根据本船的动力学方程,控制本船按上述航向行驶。
上述过程是不断进行的,具体计算的采样时间可根据船速来适当设定,因此该采用方法可使本船避开移动或固定的障碍物。根据这些描述,该过程连续进行,直到本船恢复到计划航线。若所有的参数已被调节好,则整个过程无需人为干预,可自动进行,计算机模拟的结果显示该方法是有效的。
1 问题描述
所描述的船舶避碰问题见图1,在t时刻, 本船O以速度Vo按照计划航线OB运动, 目标船P1,P2,…,Pi随机出现在水面上, 分别以速度VP1,VP2,…,VPi在水面做匀速直线运动。针对该情境,设计一种自动避碰方法,满足以下要求。

图1 船舶避碰问题
1) 自动分析来船和本船碰撞的可能性及风险,决定本船是否需要采取避碰措施。
2) 计算本船O和最危险目标船Pi可行的相对避碰方向,并由此反向推算在保持本船速度不变的情况下,本船可行的避碰速度方向。
3) 控制本船按可行的避碰速度方向行驶,并在完成避碰过程后使本船O恢复到计划航向上。
4) 上述算法要随时间连续不断地进行,直到航行结束,且来船数目不影响算法的一般性。
该方法集中解决船舶避碰的主要问题,暂不考虑外部环境扰动力(如风、浪、流力)和国际避碰规则。问题的重点是在探索静水中自动避开多个运动来船。在此基础上,稍微改变约束条件,可以解决满足上述更一般的约束和外部条件的问题。
2 船舶运动数学模型
用船舶运动数学模型中最常用的MMG(Manoeuvring Model Group)模型来计算本船的实时速度和位移。以下详细描述一个三自由度,用于描述水面运动船舶纵荡、横荡、艏摇运动的MMG模型。为方便计算,该模型采用一撇系统来实现变量的无量纲化,并将方程放在地球固定坐标系中统一处理。
(1)
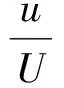
螺旋桨的推进力XP的计算式为
(2)
式(2)中:ctp和tP0为相关的常数,由试验测定;n为螺旋桨的转速;DP为螺旋桨的半径。
舵力XR,YR和舵力矩NR的计算式为
(3)
(4)
(5)
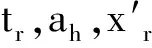
作用在船体上的外力XH,YH和外力矩NH用 Inoue 模型,然后根据式(6)将船体坐标系转换为大地坐标系。
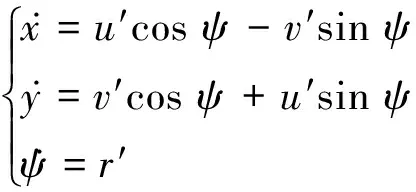
(6)
联合式(1)和式(6)即可求出本船任意时刻的速度和位置,所有的目标船都按匀速直线运动。
考虑到简单而不失一般性,目标船作为可能的碰撞目标都假定为圆形,并满足式(7)。
(xc-xf)2+(yc-yf)2=R2
(7)
3 基于速度障碍的本船避碰方向计算
船舶自动导航的核心问题避碰也是一个目标航向不断变化的航向跟踪问题,而可行航向由不同的船舶会遇形势来决定。这里通过引入速度障碍的概念,提出一种自然、简单的避碰方法,将动态障碍物避碰问题转化为静态障碍物避碰问题,并对其求解。

图2 速度障碍
由图2可知,该方法的基本思想为:A和B分别为本船和目标船;VA(t)和VB(t) 分别为t时刻两船的速度向量;VAB(t)为t时刻A相对于B的速度。若B是静态目标, 则VB(t)=0, 显然,若VA(t)的方向落入∠B1AB2的范围内,则A将会与B发生碰撞;否则,若B是移动目标, 则VB(t)≠0, 若VAB(t)的方向落入∠B1AB2区域,则A将不可避免地与B发生碰撞。下面首先给出速度障碍的定义,然后根据不同的会遇形式设计避碰算法。
定义1A相对于B的速度障碍区CAB(t)为
CAB(t)={VAB(t)|LAB∩B≠φ}
(8)
式(8)中:CAB(t) 为图2中的三角形区域B1AB2。
定义2速度障碍VO(t)为
VO(t)=CAB(t)⊗VB(t)
(9)
式(9)中:⊗ 为闵科夫斯基向量加和。
若本船与n个不同的目标船会遇,且每个目标船均是匀速直线运动,则第i个目标船应满足
(10)
式(10)中:xi0和yi0为第i个目标船的初始位置;ui和vi为第i个目标船沿x轴和y轴的初始速度。由此知,VOi(t) 为本船相对于第i个目标船的速度障碍, 总的速度障碍VO(t) 为本船相对于n个不同的目标船的速度障碍VOi(t)的并集。
(11)
若本船的速度不会导致碰撞,即VA(t)∉VO(t),则
(12)
式 (12) 为多船避碰的充分条件,但其只是一个形式化表达,如何在具体的会遇形势下计算VOi(t)是问题的关键。图3中假设O为本船,Pi为目标船,则基于速度障碍的船舶避碰方法可有以下表述。

图3 多船避碰
1) 讨论圆与直线相交的条件,若直线y=ax+b与圆 (x-c)2+(y-d)2=r2联立有解,则二者相交,设判别式函数
delta(a,b,c,d,r)=a2(r2-c2)+(d-b)(2ac-
d+b)+r2
(13)
式(13)中:若delta≥0,则表明圆与直线相交。
2) 根据标准判断某目标是位于本船的前方还是后方,“前”或“后”是一个与本船随时间运动的方向有关的量。假定本船在t-1时刻位于A(a1,b1),t时刻位于B(a2,b2),判断点C(a3,b3)在t时刻是位于本船前方还是后方的依据如下。
作一条过A点垂直于AB的直线,其方程为
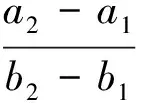
(14)
若B点和C点均位于该直线的同侧,则C点在目标的前方,否则在后方,前提是采样间隔时间很短,船舶在此时间段内可能运动的距离不会超过目前到此直线的距离。定义函数

(15)
式(15)中:若fd>0,则位于本船前方;否则fd<0,位于本船后方。
在上述2个判断函数的基础上,采用相对运动速度障碍设计自动避碰算法如下。
1) 根据式(1)和式(6),采用龙格-库塔方法计算本船O在t时刻的位置坐标(x(t),y(t)) ,根据其匀速直线运动方程计算第i个目标船Pi的位置坐标(xi(t),yi(t)) 。
2) 根据上述位置坐标,计算∠P1OC,∠P2OC,…,∠PnOC。
∠PiOC=
(16)
式(16)中:i=1,2,…,n;Ri为第i个目标障碍物的半径。
3) 按升序排列∠PiOC,即 ∠Pi1OC<∠Pi2OC<…<∠PinOC,并因此重新排序下标为i1,…,ij,…,in,j=1,2,…,n。
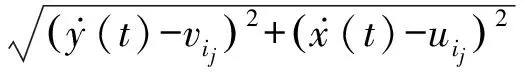
5) 采用式(13)判断相对速度线OPij是否与目标障碍物Pij所在的圆相交,若相交,则继续由式(15)来确定目标是否位于本船前方。若既相交又位于前方,则可确定本船与目标船按目前状态航行会相撞,否则返回式(4) ,j=j+1。
6) 若本船O与目标船Pi1可能碰撞(如图3),则考虑与其最相近的左右两艘船,将会有以下4种会遇态势。
A1. 左侧速度障碍区重叠:∠Ai1OC>∠Bi1+1OC且∠Bi1OC>∠Ai1-1OC。
A2. 右侧速度障碍区重叠:∠Ai1OC<∠Bi1+1OC且∠Bi1OC<∠Ai1-1OC。
A3. 两侧速度障碍区重叠: ∠Ai1OC>∠Bi1+1OC且∠Bi1OC<∠Ai1-1OC。
A4. 两侧都可以通过:∠Ai1OC<∠Bi1+1OC且∠Bi1OC>∠Ai1-1OC。
具体判断方法为:以A1为例,根据式(14)判断直线OAij是否与障碍物圆Pij+1相交,以此确定是否左侧重叠。否则j=j+1, 直至j=n。
7) 计算避开速度障碍区本船的速度方向角,方法如下。
首先根据不同的会遇态势确定能避开速度障碍区的最小变化的相对速度角∠VOPi1,用θd表示;然后根据相对速度角方程来求解可避开障碍区的本船速度角βd。

(17)
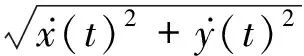
(18)
根据4种不同的会遇态势,若要以最少的转向实现避碰,则可设定相对速度角为:A1,θd=∠Bi1OC; A2,θd=∠Ai1OC; A3,速度角选择为最接近当前航向角的那一侧,具体为
A4, 若∠Bi1OPi1<∠Ai1OPi1, 则θd=∠Ai1OC,否则θd=∠Bi1OC。
可由固定速度值V不变求合适的速度角βd,也可由固定速度角βd求合适的速度值V。由于速度角更易控制,这里选择前者,则解式(17), 设
Δ=[V2(1+tan2θd)+2uivitanθd-
(19)
若Δ>0, 则本船的速度角βd有2个解
(20)
则可取速度角为
(21)
4 航向控制和恢复
为最终实现避碰,还需控制本船的速度方向。当船转向不大时,漂角较小,速度方向可近似等同于航向。若要直接控制速度方向,则将航向ψ换成速度方向即可。有许多方法可实现船舶航向控制,例如PID 控制、预测控制、自适应控制及神经网络控制等等。考虑到一般性和实用性,这里采用最常用的PID控制来求解该问题。首先考虑舵机的动力学和舵角的限制问题,一般来说,舵机满足
(22)
式(22)中:δ(0)=δ0;δe为指令舵角;δ为实时舵角;Te为时间常数;Ke为舵机增益常数。通常,舵角的实际值限制在 -δmax≤δ≤δmax,这里
δmax=35°
(23)
为满足上述条件,同时保持舵角的连续、光滑、可导,可用一个双曲正切函数对指令舵角做以下变换
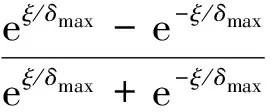
(24)
则用变量ξ⊂(-∞,+∞)替换了命令舵角变量δe⊂(-δmax,δmax), 然后用增量式PID控制算法使本船保持在航向βd上。
当本船O按上述算法驶过与目标船Pi的最近会遇点之后,开始恢复到计划航线上,因此需不断计算最近会遇距离,当两船间距离最小时,设定航向变为计划航向并送到该控制模块。
5 仿真模拟及结果讨论
利用经典的Mariner标准船做模拟,其主要船型的参数为:船长171.8 m,型宽23.17 m,设计型深8.23 m,设计排水量18 541 t,设计速度15 kn。其他参数详见文献[12]。
本船在大地坐标系下的初始位置为(0,0),初始速度为15.44 kn。在以下模式试验中,每个目标船被设定为半径为200 m的圆,目标船的初始位置和速度是随机的,依赖于不同的船舶会遇态势,详见表1~表2。

表1 会遇态势 A1

表2 会遇形势A2
本船的PID控制参数设定为:KP=6,KI=400,KD=6。为简化,仅显示A1和A2两种会遇态势下的模拟结果(见图4和图5)。
通过观察上述仿真结果可知:本船可在上述模拟的会遇态势下实现与目标船的避碰,但是实际避碰效果与以下3个因素有关。

图4 A1下的模拟结果
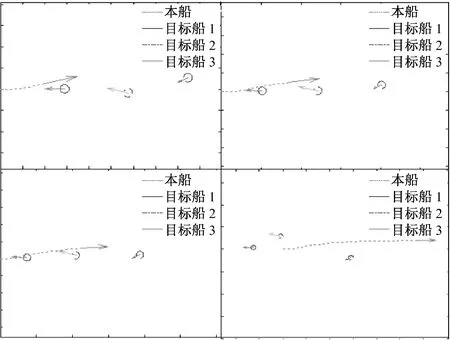
图5 A2下的模拟结果
1) 本船与目标船间的距离(越长则本船越安全)。若距离太短,则本船与目标船发生碰撞的风险会大大增加。在实际航行中,本船的避碰操作执行越早越安全,但执行得太频繁或太早会浪费燃油,因此设定一个合适的避碰起始距离很重要,通常根据经验把该距离设定为5 n mile,即小于此距离才开始启动本系统。
2) 理论上该方法可根据会遇船舶的实时位置来判断当前的会遇态势,并随着时间连续地进行判断,由此持续计算可行的相对速度方向,然后求解相对速度方程得到本船当前可行的避碰速度,并将其送到PID控制模块。但是在实际情况中,由于各种外部干扰的存在,来船和本船实际位置的判断会出现偏差,因此也会出现判断失误的情况。
3) 本船PID航向控制的效果。 要实现船舶的避碰,不仅要计算出可行的避碰路径,而且要控制船舶按该路径运动。因此,若本船航向控制的效果很差,则即使算出了可行的避碰方向,避碰效果也不会好。本船的航向控制可用任意一种方法,不一定是PID控制,但是无论用哪种方法,都要仔细调节控制参数以达到满意的控制效果。
前述算法的描述都是基于船舶运动模型及所有参数已知的前提下得到的。因此,若要设计实用的自动避碰系统,就必须事先测得船舶所有水动力参数并将其输入系统,或安装一套实时的船舶水动力参数估计系统,并将其与自动避碰系统联合起来,只有如此,才能真正实现“自动航行”。
[1] 郑中义, 吴兆麟. 转向避让的最后机会模型及其应用[J].大连海事大学学报,2001,27(2):6-10.
[2] 郑中义, 吴兆麟. 船舶碰撞危险度的新模型[J].大连海事大学学报,2002,28(2):1-5.
[3] 李丽娜, 王俊玲, 陈国权. 船舶拟人智能避碰决策理论的集成机器学习策略[J].信息与控制,2011,40(3):359-368.
[4] 李丽娜, 熊振南, 高岩松, 等. 单船避碰智能决策的生成与优化方法[J].中国航海,2002(2):49-52.
[5] SMIERZCHALSKI R, MICHALEWICZ Z. Modeling of Ship Trajectory in Collision Situations by an Evolutionary Algorithm[J]. Evolutionary Computation, IEEE Transactions on, 2000, 4(3): 227-241.
[6] TSOU M C, KAO S L, SU C M. Decision Support from Genetic Algorithms for Ship Collision Avoidance Route Planning and Alerts[J]. Journal of Navigation, 2010, 63(1): 167-182.
[7] ITO M, ZHNNG F, YOSHIDA N. Collision Avoidance Control of Ship with Genetic Algorithm[C]//Control Applications, 1999. Proceedings of the 1999 IEEE International Conference on. IEEE, 1999.
[8] LEE H J, RHEE K P. Development of Collision Avoidance System by Using Expert System and Search Algorithm[J]. International Shipbuilding Progress, 2001, 48(3): 197-212.
[9] LIU Y H, YANG W L. The Structure Design of an Intelligent Decision Support System for Navigation Collision Avoidance[C]//Machine Learning and Cybernetics, 2004. Proceedings of 2004 International Conference on. IEEE, 2004.
[10] IIJIMA Y, HAGIWARA H, KASAI H. Results of Collision Avoidance Manoeuvre Experiments Using a Knowledge-Based Autonomous Piloting System[J]. Journal of Navigation, 1991, 44(02): 194-204.
[11] FIORINI P, SHILLER Z. Motion Planning in Dynamic Environments Using Velocity Obstacles[J]. The International Journal of Robotics Research, 1998, 17(7): 760-772.
[12] FOSSEN T I. Guidance and Control of Ocean Vehicles[M]. New York: Wiley, 1994:431-432.
Multi-ShipCollisionAvoidingControlConsideringVelocityObstacle
XIONGYong1,2,HEYixiong1,2,HUANGLiwen1,2
(1. School of Navigation,Wuhan University of Technology,Wuhan 430063,China;2. Hubei Inland Shipping Technology Key Laboratory,Wuhan 430063,China)
Ordinary collision avoidance calculation is not fit for automatic control operation because it designs feasible avoiding routes according to the relative positions and speeds of targets without considering the manoeuvreability of own ship. A practical multi-ship collision avoidance control strategy is proposed which plans collision avoiding route according to the relative velocity direction and own ship motion control simultaneously. This method contains three main steps: 1. calculating basic motion and position parameters of own ship and target ships; 2. calculating real time feasible velocity direction of own ship based on the velocity obstacle; 3. proceeding to do control variable transformation and control algorithm design. This method allows real time multi-ship collision avoidance. Simulating experiments show promising results and is flexible and easy to implement. Some suggestions are given for further study.
waterway transportation; automatic collision avoidance; ship motion mathematic model; velocity obstacle; PID control
2015-04-19
国家自然科学基金(51379170);中央高校基本科研业务费专项资金(133212003);湖北省自然科学基金(2014CFB878)
熊 勇(1976—),男,湖北黄冈人,副教授,博士,从事舰船运动控制研究。E-mail:bear_brave@163.com
1000-4653(2015)03-0046-06
U675.96
A

