LNG储罐在地震作用下弹性罐壁Mises应力理论解
侯钢领,张春龙,2,贾晓飞,宋天舒
(1.哈尔滨工程大学 航天与建筑工程学院,黑龙江哈尔滨150001;2.中国核电工程有限公司,北京100000)
LNG储罐的地震响应由于涉及流体与固体的耦合,导致该类结构的动水压力计算复杂[1-2],难以直接应用到实际工程中。国内外广大学者[3-4]的研究大多数是基于有限元法研究动水压力,比如清华大学的胡盈辉和庄茁[5]提出的附加质量法,把动水压力转化成附加质量作用到罐壁上,实现流固耦合解耦;杜显赫[6]和孙建刚[7]等人通过液体势能函数的建立,进而考虑其流固耦合作用,但其数值模拟结果是建立在经验判断上,缺乏理论依据。本文提出了一种从理论上计算弹性壁储罐罐壁Mises应力的计算方法,从而为有限元求解及工程实际应用提供定量评估。
1 我国规范与欧洲规范计算动水压力
1.1 我国规范的动水压力计算公式
我国规范是基于居荣初和曾心传等学者的研究成果[1],并采用反应谱方法。我国规范给出的圆柱形容器的动水压力计算公式为
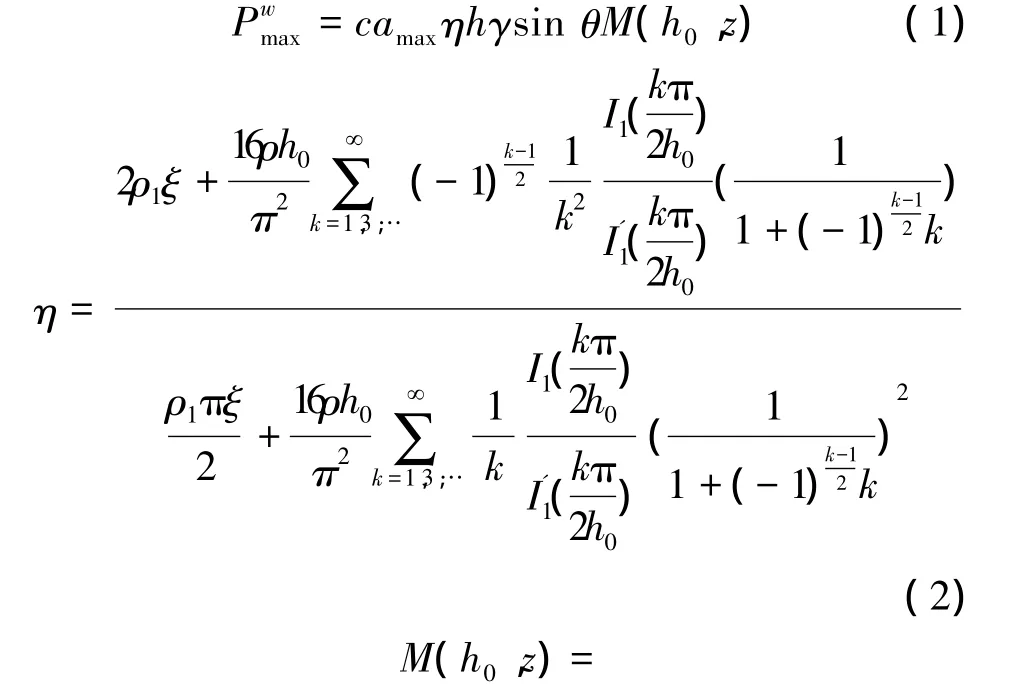
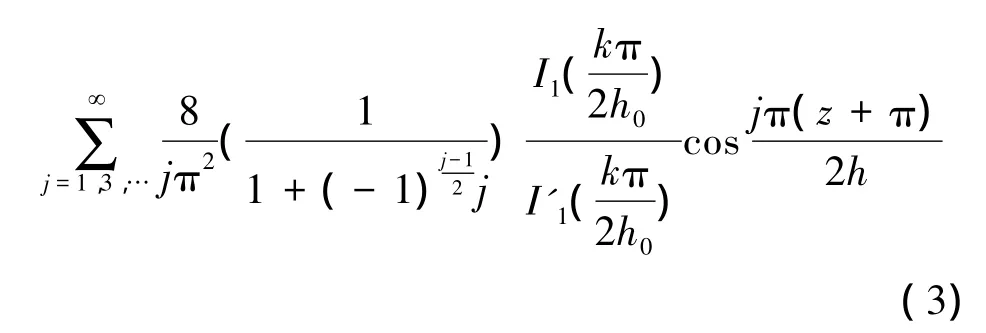
1.2 基于欧洲规范动水压力计算公式
欧洲LNG储罐的现行规范《欧洲钢制常压立式圆筒形储罐抗震鉴定标准》(BS EN 1998-4:2006),该规范将弹性壁储罐动水压力分解为:脉冲压力、对流压力和柔性压力3个部分,分别为:
储罐内任意一点所受到的脉冲压力为

储罐内任意一点所受到的对流压力为
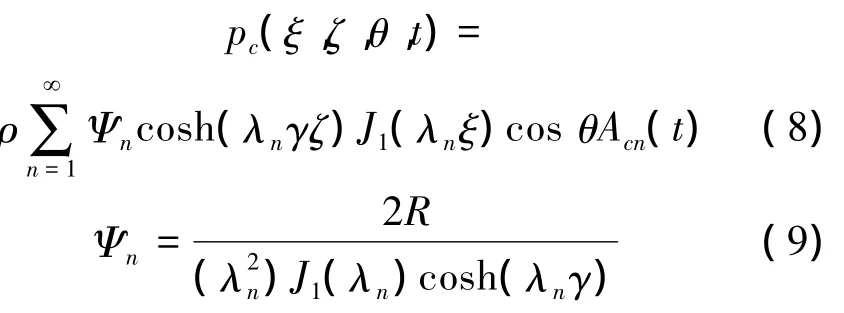
储罐内任意一点所受到的柔性压力为
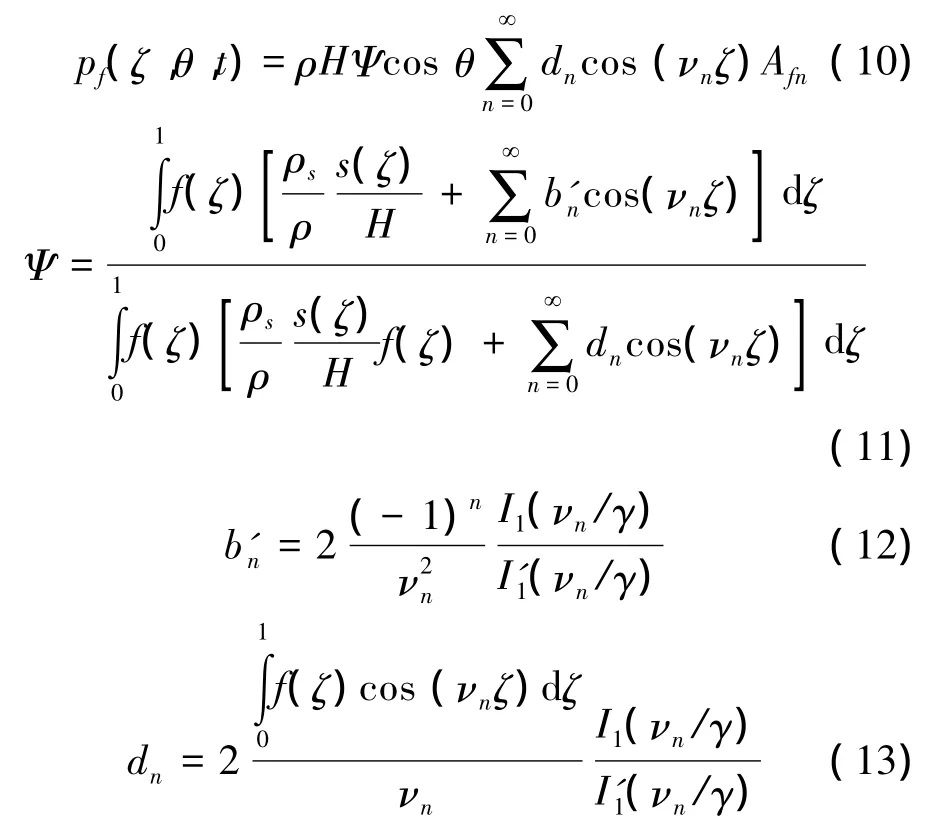
式中:H储罐内液高,R为储罐半径,ρ为储液密度,ρs为储罐密度,θ为沿环向任意角度,s(ζ)为罐壁厚度,Ag(t)为地震加速度,Acn(t)为自由振荡的单自由度加速时程响应,Afn(t)为n阶阻尼加速度响应,f(ζ)为储罐装有液体时的一阶振型函数(设f(ζ)=sinπz/2H),J1为第一类贝塞尔函数,如图1所示。
脉冲压力与对流压力合力即是刚性壁动水压力,而以上3个压力合力即是弹性壁动水压力。
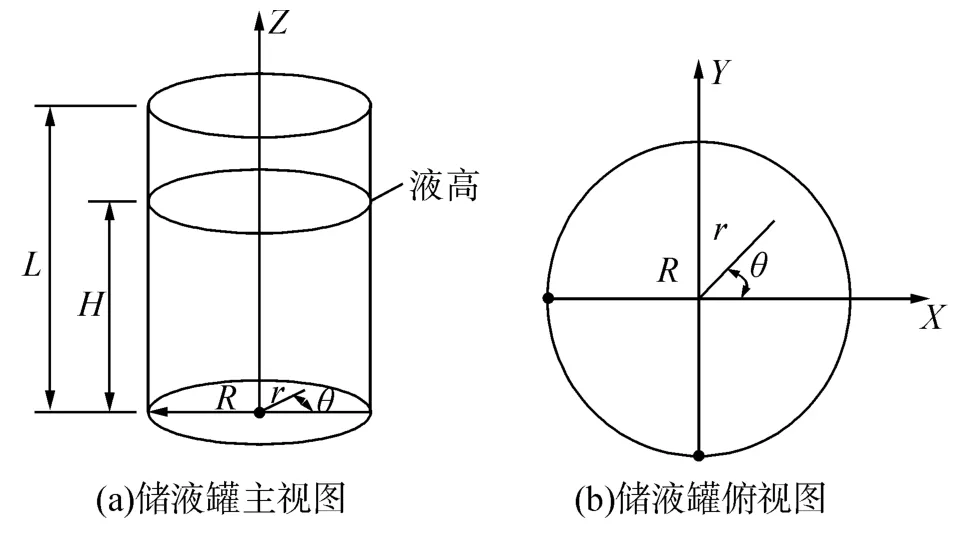
图1 储液罐几何模型Fig.1 Geometric model of the tank
2 弹性罐壁Mises应力理论解
2.1 圆柱壳的基本方程
圆柱壳中曲面的一部分[8],如图2所示,其中BC为母线方向,DE为准线方向,它们是中曲面上的一组曲率线族。取母线作为x线,准线作为φ线,以任意一曲率作为参考轴,于是中曲面上任一点A的位置可以用(x,φ),其中x为沿母线方向的线性长度,而φ为两条法线之间的夹角。
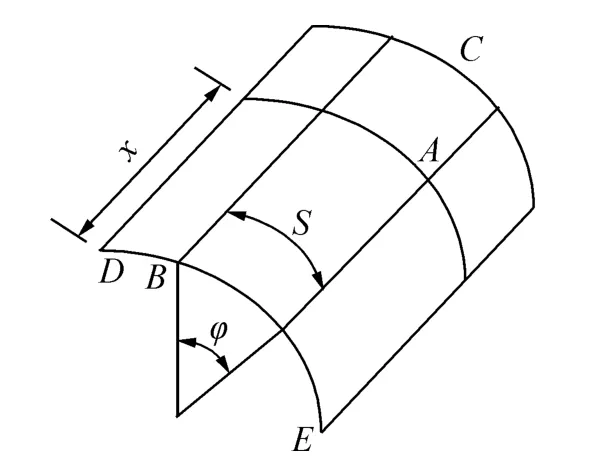
图2 圆柱壳示意图Fig.2 Diagram of cylindrical shell
3个位移分量u、v、w来表示一般情况下圆柱壳的基本方程,设其半径为a,则R=a=const,并引入无量纲量ξ=x/a,β=h2/12a2,分别用角标1、2来代替x、φ方向,3方向为垂直于罐壁的方向,则基本方程如下:

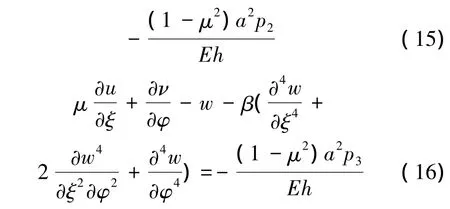
与其对应的内力表达式为

式中:E为弹性模量,μ为泊松比,h为罐壁厚度。
如果已知动水压力的三维空间分布,且在满足给定的边界条件下,求解方程组(14)~(16)可得到位移分量的解。将位移分量代入到式(17)~(22),可得到各内力素。但由于动水压力公式比较复杂,如果将动水压力公式直接代入到方程组中进行求解,计算量将非常大,并且难以解出。
在此,研究欧洲规范中的动水压力规律,即分析研究在不同情况下,同一水平面和随高度变化2种情况下动水压力的分布。发现其规律为:在同一水平面上,弹性壁储罐的动水压力可近似为正弦分布;而随高度变化,最大动水压力的分布也可近似正弦变化。应用对比分析和拟合分析,函数形式Y=Psin(Ax+B)sin(πφ/φ0)可以与弹性壁储罐动水压力值进行很好的拟合[9],并将此代替动水压力计算公式代入上述方程中进行求解。
2.2 静水压力作用下圆柱壳有矩理论
圆柱壳在静水压力作用下,薄膜内力起主导作用,但是圆柱壳底部的弯矩也非常大,不容忽视。现考虑薄膜内力与弯曲共同作用情况下圆柱壳内力表达式如下:

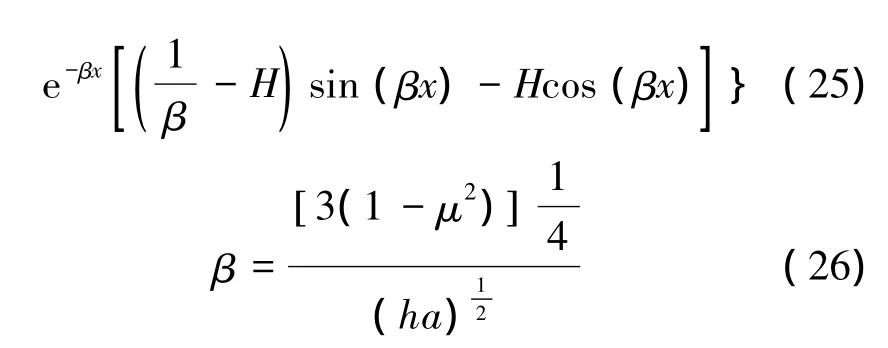
式中:H为液面高度,γ为液体重度,μ为泊松比,a为储罐半径,h为储罐壁厚度。
分别将静水压力与动水压力作用下罐壁的应力进行叠加,最后便可求解出弹性壁储罐在地震作用下罐壁的Mises应力。
3 LNG储罐算例
3.1 LNG储罐弹性罐壁Mises理论解
将LNG储罐简化计算取半径a=40 m,罐高L=30 m,液高H=30 m,弹性罐壁厚h=0.02 m。内罐材料为钢材,密度为 ρs=7.85 × 103kg/m3,弹性模量为E=2.1 × 1011Pa,泊松比 μ =0.3,屈服强度为500 MPa。液体密度 ρ=0.48 × 103kg/m3。
假设储罐建造地区为II类场地,设计地震分组为第2组,抗震设防基本烈度为8度。选用EL Centro波和Manual波2组地震波进行时程分析,峰值加速度为0.7 m/s2;EL波的峰值加速度出现时间为2.12 s;Manual的峰值加速度出现时间为 6.26 s,如图3所示。
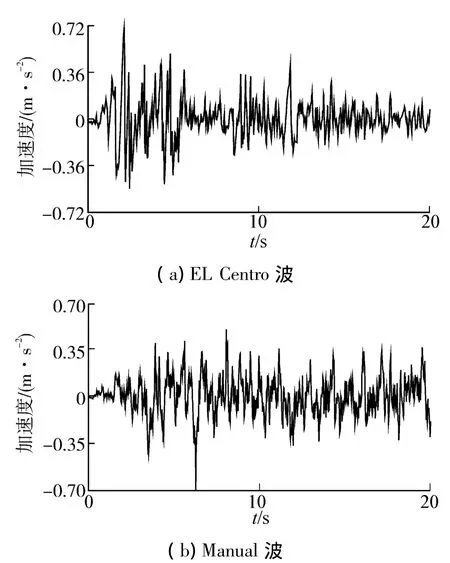
图3 地震波加速度时程曲线Fig.3 Time history curve of seismic wave acceleration
比较我国的反应谱法与欧洲规范的动水压力。在水平夹角为0°,在峰值加速度时刻弹性壁储罐动水压力沿高度方向的分布,如图4所示。从图4可以看出:我国的规范方法在计算储液上部起主导作用的对流压力部分以及储液下部起主导作用的脉冲压力部分明显偏小。在此,采用欧洲规范为依据,计算静、动合压力作用下弹性罐壁Mises应力。
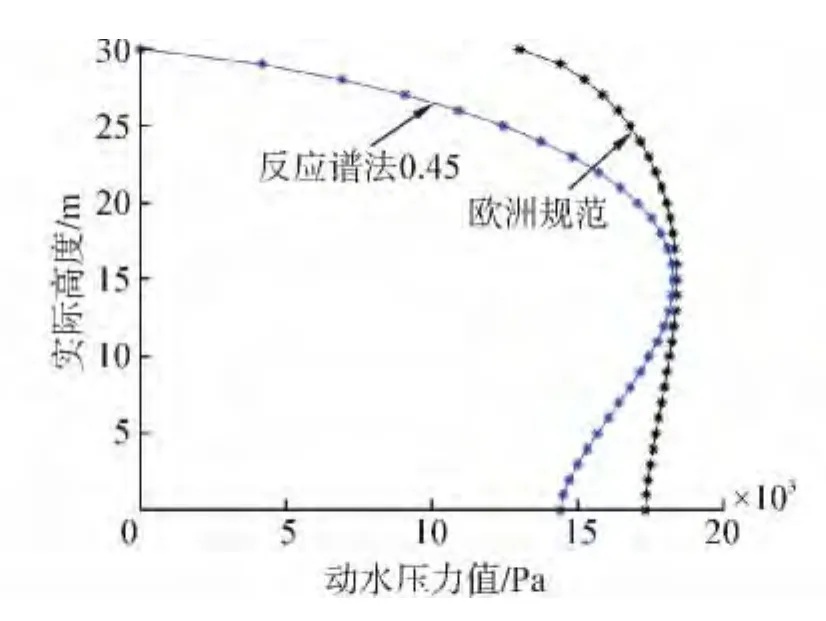
图4 反应谱法与欧洲规范对比图Fig.4 Result comparison between response spectrum method and European standard
根据式(4)~(13),并应用MATLAB软件实现了弹性壁储罐分别在EI波和Manual波峰值加速度作用时的动水压力空间分布,见图5和图6所示。图6为静水和动水压力合力的三维空间图。应用拟合函数形式Y=Psin(Ax+B)sin(πφ/φ0)和最小二乘法,得到P=18 586.7,A=0.038,B=7.39,φ0=π 。

图5 弹性壁储罐动水压力值Fig.5 Hydrodynamic pressure on elastic wall
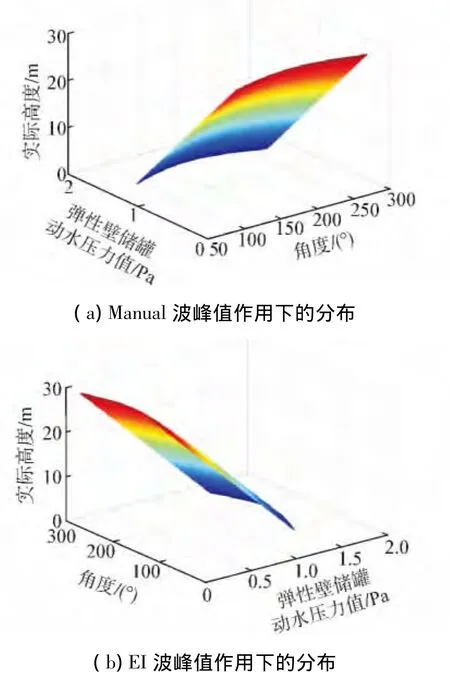
图6 弹性壁储罐静动合压力值Fig.6 Hydrodynamic and hydrostatic pressure on elastic wall
图7为进行曲线拟合精度的对比。可以看出,拟合曲线除在最低点的误差为4%以外,其余点的误差均小于3%,最大为2.89%,平均误差为1%,说明曲线拟合已经达到精度要求。

图7 计算数值与曲线拟合对比Fig.7 Contrast between numerical result and curve fitting
根据方程组(13)~(16),可知P1=0,P2=0,P3=Psin(Ax+B)sin(πφ/φ0),设 3 个位移分量如下:
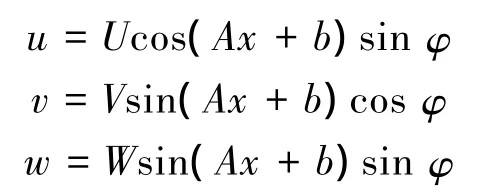
它们满足所有的位移方程,同时也满足了四边简支的边界条件,其中U、V、W是需要计算的未知参数,再将P1、P2、P3和 3个位移分量代入式(13)~(16),化简后得方程组:
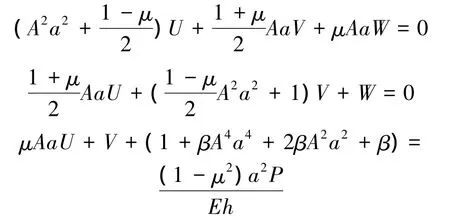
求解上述方程组,得到位移分量U=0.000 6,V=-0.008 3,W=0.014 5。将上面 3 个位移分量代入到式(17)~(22),可得到简后得弹性壁储罐在动水压力作用下的内力公式:

取单位长度,b=1,由上面动水压力作用下的弹性罐壁内力公式得到
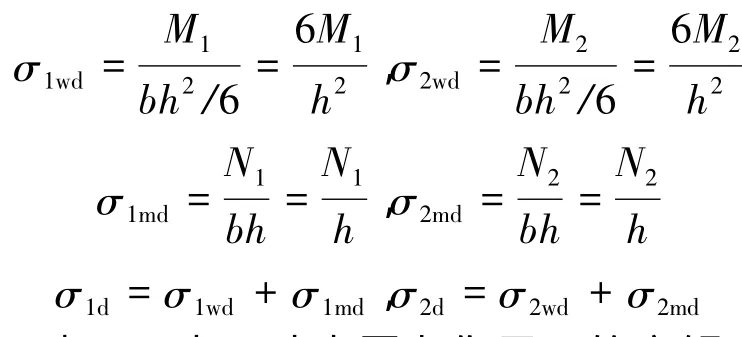
式中:下标wd表示动水压力作用下的弯矩,md为动水压力作用下的膜应力,d代表动水作用。
同理,由式(23)~(26)静水压力作用下的弹性罐壁内力公式得到
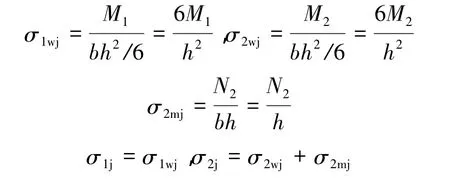
式中:下标wj表示动水压力作用下的弯矩,mj为动水压力作用下的膜应力,j代表静水作用。
则由上面公式得到弹性罐壁在地震峰值加速度作用下的主应力分别为

最后得到弹性罐壁在地震峰值加速度作用下的Mises应力为

由于自重影响相对于静水压力和动水压力的影响很小,自重影响可以忽略不计。上述弹性罐壁的Mises应力计算未考虑弹性罐壁自重的影响。
3.2 耦合欧拉-朗格朗日(CEL)算法
ABAQUS中的CEL算法是完全的流固耦合算法,分析类型为动态显示,具有较高的计算精度,并且已经成为检验理论简化解的重要工具。流体构型通过计算流体在欧拉单元中所占的体积分数确定。流体材料可以在欧拉单元之间流动,并与固体单元相互作用。计算模型时需要一个足够大的欧拉网格,能够将固体单元可能移动到的所有位置全部包裹在内,由于CEL计算量较大,所以模型采用对称建模方式如图8所示,取一半模型进行分析。罐壁单元尺寸为0.8 m,欧拉体单元尺寸为 0.8 m,如图 9 所示。

图8 LNG储罐整体模型Fig.8 Model of LNG tank

图9 LNG储罐网格划分Fig.9 Meshing model of LNG tank
4 计算结果及分析
针对上节算例,分别计算在EI波和Manual波峰值加速度作用下,弹性罐壁在0°和180°位置罐壁的Mises应力随高度的变化,如图10~13所示。
因为罐壁Mises应力起主导作用的位置主要在中下部[10],所以本文提取了罐壁0~15 m的Mises应力随高度变化的数值,从图10和图12可以看出,罐壁Mises应力随高度的变化为底部大致呈正弦变化趋势,再往上则逐渐成线性变化趋势,罐壁底部的正弦变化趋势主要是由于静水压力作用时罐壁弯曲应力引起的,而再往上的线性变化趋势则是由罐壁的膜应力所引起的。
从图中还可以看出,对罐壁Mises应力起主导作用的是静水压力,而非动水压力;弹性储罐在EI波作用时罐壁最大Mises应力在底部,理论计算数值为 461.14 MPa,仿真数值为 483.5 MPa,最大 Mises应力出现时间为3.5 s滞后于峰值加速度1.38 s。Manual波作用时,罐壁底部最大Mises应力理论计算数值为 461.14 MPa,仿真数值为 483.175 MPa,最大Mises应力出现时间为4.7 s,提前于峰值加速度1.56 s。
在Manual波作用下,弹性储罐罐壁最大Mises应力出现时间提前于峰值加速度时间其原因如下。分别对EI波和Manual波加速度时程曲线进行傅里叶变换,可以得到加速度频谱曲线如图14~15。
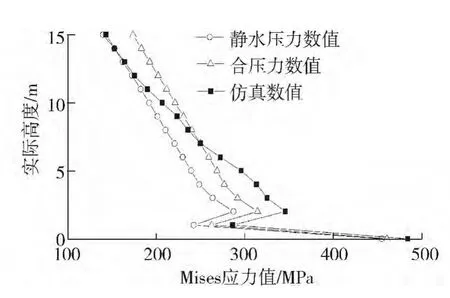
图10 EI波对比0°Fig.10 Comparison results under EI wave at 0°

图 11 EI波结果 t=3.5 sFig.11 Computing results under EI wave on 3.5 s

图12 Manual波对比180°Fig.12 Comparison results under Manual wave at 180°

图 13 Manual结果 t=4.7 sFig.13 Computing results under Manual wave on 4.7 s

图14 EI波频谱曲线Fig.14 EI spectrum
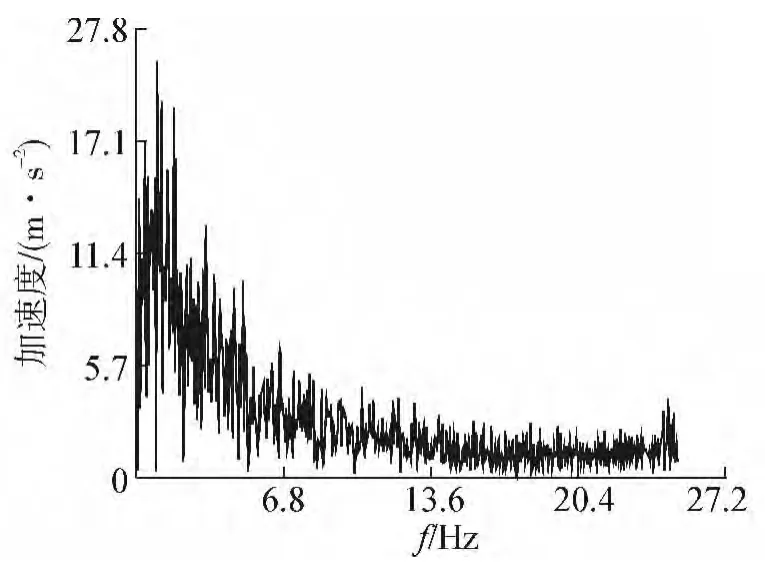
图15 Manual波频谱曲线Fig.15 Manual spectrum
通过对频谱特性[11]分析可知,EI波前20 s的卓越频率为 1.785 7 Hz,前 3.5 s 的卓越频率为 1.785 7 Hz。而 Manual波前20 s的卓越频率为3.083 Hz,前4.7 s的卓越频率为 3.756 Hz。
根据文献[12-14],储罐满液时的自振频率为

式中:fT为空罐子时的自振频率;R为储罐半径;ρ为储液密度;h为罐壁厚;ρs为储罐密度;β值查表,本文中 β 取 0.23。
5 结论
本文通过对LNG罐壁Mises应力理论计算与有限元仿真结果相对比,得出结论:
1)基于我国反应谱法计算出的弹性壁储罐的动水压力在储液上部的对流压力值和储液下部的脉冲压力值都偏小。
2)通过弹性罐壁Mises应力随高度变化的趋势图中可以看出,对罐壁Mises应力起到主导作用的是静水压力对罐壁的作用,而非动水压力。
3)弹性罐壁Mises应力随高度变化的趋势为底部大致呈正弦趋势,此主要是由于静水压力作用部分对罐壁的弯曲应力引起的。往上则逐渐呈线性变化趋势,此主要是由于罐壁的膜应力所引起的。所以弹性罐壁Mises应力在底部起主导作用的是罐壁的弯曲应力,而再往上则罐壁的膜应力逐渐起到主导作用;
4)当地震加速度的卓越频率与储液罐的自振频率比较接近时,导致储液罐出现共振或亚共振状态时,会造成罐壁最大的Mises应力提前于地震峰值加速度出现。
[1]居荣初,曾心传.弹性结构与液体的耦联振动理论[M].北京:地震出版社,1983:40-48.
[2]SH/T 3026-2005钢制常压立式圆筒形储罐抗震鉴定标准[S].上海:中国石化出版社,2006.
[3]MOSLEMI M,KIANOUSH M R.Parameter study on dynamic behavior of cylindrical ground-supported tanks[J].Engineering Structures,2012,42:214-230.
[4]MALEKI A,ZIYAEIFAR M.Damping enhancement of seismic isolated cylindrical liquid storage tanks using baffles[J].Engineering Structures,2007,29(12):3227-3240.
[5]胡盈辉,庄茁,由小川.大型储液罐在地震作用下的附加质量法研究[J].压力容器,2009,26(8):1-6.HU Yinghui,ZHUANG Zhuo,YOU Xiaochuan.Added mass approach to a large-scale liquid-storage tank under seismic excitations[J].Pressure Vessel Technology,2009,26(8):1-6.
[6]杜显赫,沈新普,刘应华.预应力LNG储罐在地震作用下的流固耦合数值模拟[C]//力学与工程应用.郑州,中国,2012:178-182.DU Xianhe,SHEN Xinpu,LIU Yinghua.Numerical simulation of fluid and structure coupling of prestressed LNG storage tank under seismic action[C]//Mechanics and Engineering Application.Zhengzhou,China,2012:178-182.
[7]孙建刚,崔利富,张营.全容式LNG储罐地震响应数值模拟研究[C]//中国国际建筑科技大会论文集.北京,中国,2010:225-230.SUN Jian’gang,CUI Lifu,ZHANG Ying.Numerical simulation of seismic response of the full capacity LNG storage tank[C]//Chinese International Building Science and Technology Conference.Beijing,China,2010:225-230.
[8]黄克智.板壳理论[M].北京:清华大学出版社,1987:137-146.
[9]史洁玉,孔玲军.MATLAB R2012a超级学习手册[M].北京:人民邮电出版社,2013:72-85.
[10]大崎顺彦.地震动的谱分析入门[M].田琪,译.第2版.北京:地震出版社,2008:49-58.
[11]翁智远.圆柱薄壳容器的振动与屈曲[M].上海:上海科学技术出版社,2007:3-16.
[12]翁智远,杨建中.圆柱形弹性贮液容器基频近似计算法[J].力学季刊,2000,21(3):354-356.WENG Zhiyuan,YANG Jianzhong.An approximate calculational method for fundamental frequency of elastic cylindrical liquid storage tank[J].Chinese Quarterly of Mechanics,2000,21(3):354-356.
[13]FISCHER F D,RAMMERSTORFER F G,SCHARF K.Earthquake resistant design of anchored and unanchored liquid storage tanks under three-dimensional earthquake excitation[M]//SCHUËLLER G I.Structural Dynamics.Berlin:Springer Verlag,1991:317-371.
[14]FISCHER F D,RAMMERSTORFER F G,SCHARF K,et al.Collapse of earthquake excited tanks[J].Mechanica,1988,25:129-143.

