强化思想方法教育是深化数学课堂教学改革的金钥匙

孙悦宾

【课程设计方案】

本节课出自人教版《数学》八年级上册“11.2.1三角形的内角”，主要目的是让学生掌握和理解三角形内角和定理，并会运用已有的知识证明内角和定理，然后运用定理解决实际问题.重点是掌握三角形内角和定理，而三角形内角和定理的证明是本节课的难点.采用“问题情景—探究交流—得出结论—强化训练”的模式展开教学.利用多媒体教学手段，增加教学过程的趣味性，强调学生的动手操作和主动参与，通过集体讨论、小组活动等形式，培养学生自主探究的意识.

【课堂教学实录】

一、创设情境，问题呈现

师：在△ABC中，∠A、∠B、∠C的和是多少度？

生：小学我们学过，三角形三个内角之和是180°.

师：是不是所有的三角形的内角和都是180°呢？我们能用你喜欢的方法进行验证吗？

生：（学生思考了近5分钟后）可以测量每个内角然后把三个内角的度数相加来求.

师：那好，就请你来前面给大家展示并讲解你的过程吧.（学生先画了一个三角形，然后分别测出内角度数并加相，突然发现内角和是181°.）

师：大家都看到了他的想法很好，但是结果并不让他满意，谁能用他的方法再操作一次呢？（学生用同样的方法演示一遍，得到内角之和等于180°.）

师：同学们你们有什么启示呢？三角形内角和等不等于180°呢？

生：等于180°.

生：测量本是实验的方法，任何实验都存在误差，误差是不可避免的，但可以减小.

师：那好，哪位同学还有更好的方法来验证内角和是180°呢？

生：可以用撕纸的方法验证.具体做法如下：先用卡纸剪出一个三角形，再将三个内角剪下并粘贴在一个点处，可得到一个平角，平角是180°，所以三角形内角和等于180°.（学生边说边演示.）

师：太好了，你的做法别具一格，这是你努力思考的结果，继续努力啊！

二、推理论证，合作探究

师：刚才几位同学都是通过实验的方法得出了内角和的度数，我们能不能通过推理论证的方式来证明三个内角和等于180°呢？那就请同学们以小组为单位，组内讨论的形式共同得出答案.

问题：已知△ABC中，∠A+∠B+∠C的值是多少？

师：经过同学们热烈的讨论，下面请各小组做好准备，已经准备好的直接来展示.

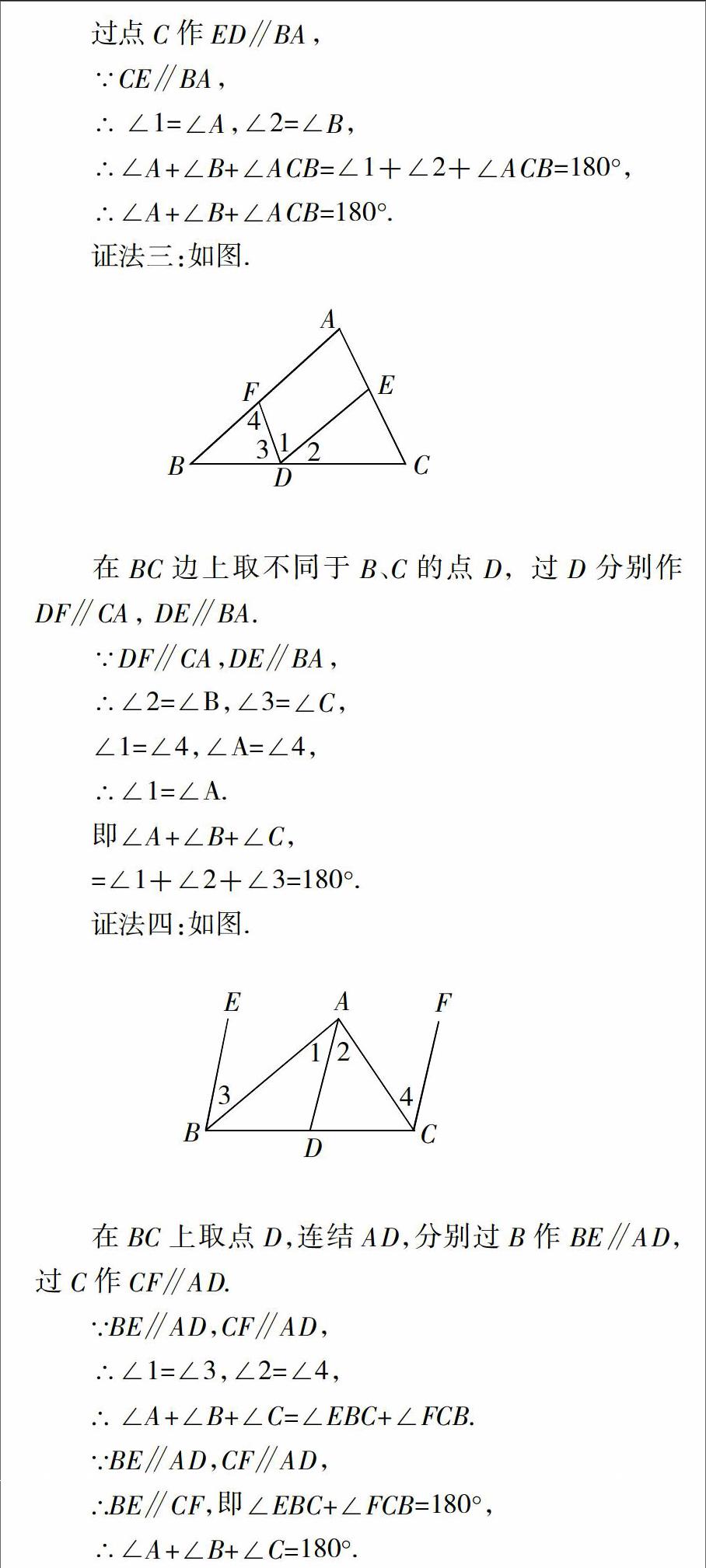
经过学生的展示教师整理四种方法如下：

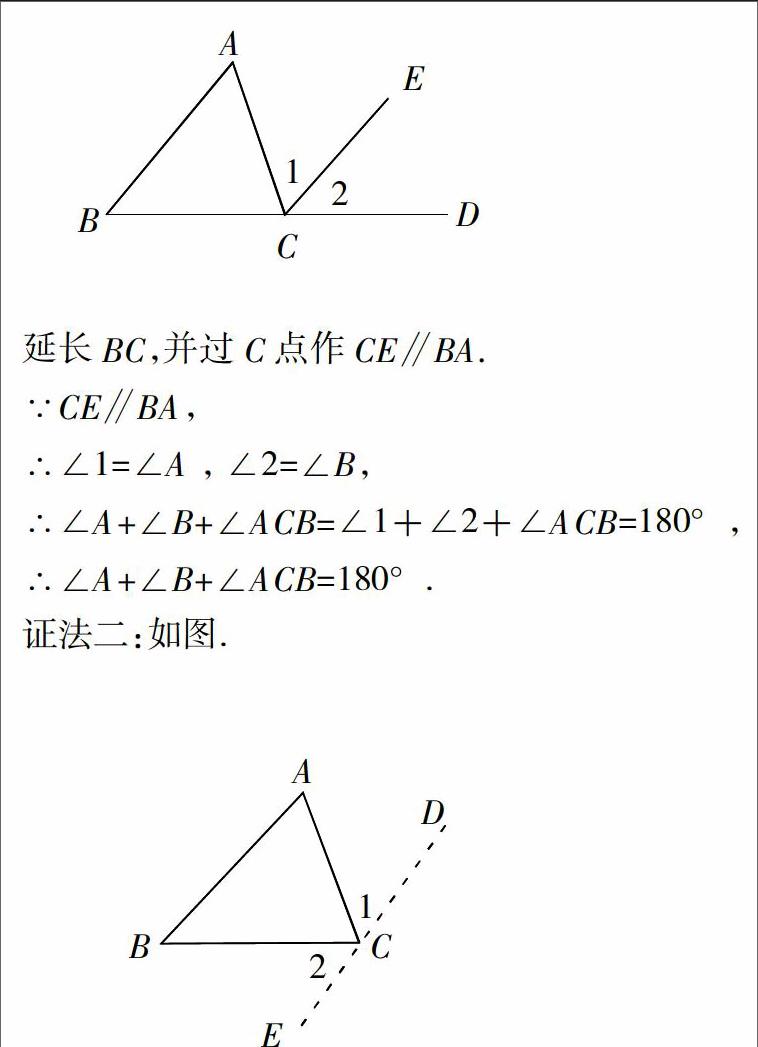
证法一：如下图.

师：刚才同学们用多种方法证明了三角形三个内角和是180°.经过同学们严密的证明我们得出本节课的重要定理.

板书：三角形内角和定理：

三角形中三个内角的和等于180°.

师：同学们，回想刚才几名同学的证明过程，你有什么启发？

生：都须要做辅助线.

生：是将三角形三个内角的和转化成一个平角，或者转化成一组平行线下的一对同旁内角.

师：很好，大家总结得很到位，辅助线是我们为了做题的方便自行加进去的直线，通常画成虚线.第二名同学无意中就总结出了一种数学思想—转化思想.

三、巩固新知，小试牛刀

师：为了检测大家对三角形内角和定理的掌握情况，我们练习几道小题：

1.在△ABC中，∠A=45°，∠B=52°，∠C= .

2.等腰三角形中，底角是顶角的2倍，求三个内角度数.

3.一个三角形中，最多 个锐角，最多个 直角，最多 个钝角，最少 个锐角？

【布置作业体现拓展】根据三角形内角和定理，请你试求四边形内角和是多少？n边形内角和又是多少呢？

四、知识梳理，总结重点

师：好了同学们，今天我们再次走进三角形，你有哪些收获要和大家分享呢？

生1：我知道了可以用测量、撕拼、折拼等方法验证三角形的内角和.

生2：我学会了如何证明三角形内角和.

生3：我明白了一个道理：众人拾柴火焰高！我也很享受讨论过程中的乐趣.

师：这节课我们先用测量、撕拼、折拼等方法对三角形内角和进行猜想并验证，然后证明得出了三角形的内角和是180°这一结论，并且大家还能运用这个结论解决一些数学问题.特别是学会了怎样添加辅助线来证明几个问题，所以引入辅助线技巧是本节课的精华所在.最后，送给大家一句话：在数学的天地里，重要的不是知道什么，而是我们是怎么知道的.

五、创新板书，便于理解

11.2.1 三角形的内角

一、探究过程：

提出问题：如何得出三角形三个内角和的度数呢？

回顾与猜想：论证：1.可以通过测量和拼图等方法获得三角形内角和为180°；2.回顾小学学过知识；3.证明.

二、探究结论：

三角形内角和定理：三角形三个内角的和为180°.

三、定理的应用：（略.）endprint