广义神经传播方程H1-Galerkin低阶 非协调混合有限元的超收敛分析

周树克,王 婷

(1. 河南城建学院 数理学院, 河南 平顶山467036；2. 南阳师范学院 数学与统计学院, 河南 南阳473061)

0 引言

神经传播方程是一类重要的非线性发展方程[1]，神经传播信号u及它关于时间和空间的变化率，在数学上呈现为上述非线性拟双曲方程[2]，其被广泛应用于生物、力学等领域， 并在理论分析和数值逼近方面取得了一些重要结果.其中，文献[3]讨论了该方程解的性质；文献[4]和[5]分别利用五节点元和带约束的Qrot元研究了该方程，并得到了O(h2)超逼近和超收敛性质；文献[6]和[7]对一类非线性广义神经传播方程利用EQrot元得到了超逼近和整体超收敛结果.

1 混合有限元的构造及性质

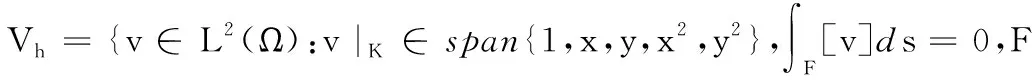
Vh⊆

是Vh上模.

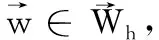
定义其范数为

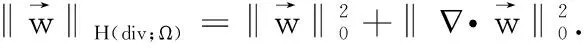
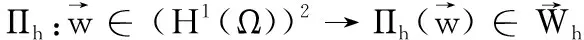
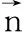
(1)

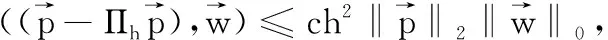
2 H1-Galerkin混合有限元的半离散格式及超逼近分析

本文讨论如下广义神经传播方程:

其中X=(x,y);Ω=R2为边界光滑的有界凸区域;u0(X),u1(X)为已知光滑函数;fu,gu均为有界函数且关于变量u满足Lipschitz 连续. 令方程(4)的变分形式为：

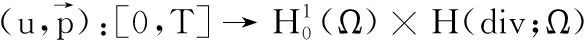
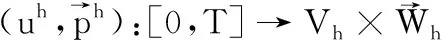
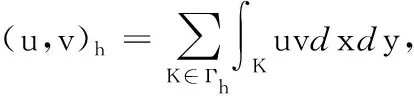
定理1 方程(6)有唯一解.

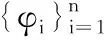
将式(7)代入方程(6)，并令vh=φj(x),(j=1,2,…,n) 可得

r(t)B=l(t)N,

(8)

其中r(t)=(r1(t),r2(t),…,rn(t))1×n,l(t)=(l1(t),l2(t),…,ln(t))1×k,B=(φi(X),φj(X))n×n,N=(ψi(X),φj(X))k×n.这是关于向量r(t)的线性方程组，因为B对称正定，所以方程(6)存在唯一解.再将式(7)代入方程(6)，并令可得

Al″(t)+Cl′(t)-Cl(t)=F(r),

(9)

这里A=(ψi(X),ψj(X))k×k,C=(·ψi(X),·ψj(X))k×k,F(r)=(fi)k×1,

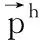
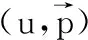
证明令

u-uh=u-Ihu+Ihu-uh=η+ξ,

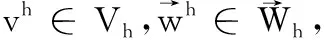
在方程(12)中，令vh=ξ, 有

方程(12)两端对t求导数,令vh=ξt,类似以上过程,可得

下面对式(16)右端分别进行估计，首先由Cauchy不等式,ε-Young不等式,再利用式(2)得

由f(u)关于u满足Lipschitz连续有界及插值理论知

同理,

将式(17)-(20)代入式(16),取适当小的ε,并利用Gronwall不等式,得

将式(14)-(15)代入式(21),得

再借助于Gronwall引理有

把式(24)代入式(14)得

证毕.

4 整体超收敛

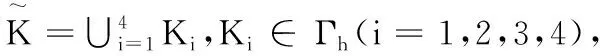
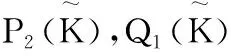
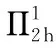
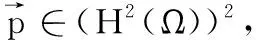
定理3 在定理1和引理1条件下，有下面的整体超收敛结果：

证明注意到

由引理1得

利用三角不等式，可得式(25).同理，利用引理2和三角不等式，可以得到式(26)的结果.证毕.

5 结语

若将本文中的EQrot元换成Q1rot元(正方形剖分情况)，或P1非协调矩形元，或带约束的旋转Q1元，本文的结果仍然成立.进一步,不难验证，若将本文的混合元换为P1-非协调三角形元，本文的超逼近和超收敛结果也成立，虽然自由度是9NP比较大，但对网格的剖分要求却宽松了.