一个离散可积族的可积耦合及其H am ilton结构

徐秀丽

(枣庄科技职业学院高级技工部，山东枣庄 277500)

一个离散可积族的可积耦合及其H am ilton结构

徐秀丽

(枣庄科技职业学院高级技工部，山东枣庄 277500)

由位移算子通过二次型恒等式直接得到离散可积族的耦合及其Hamilton结构.这种方法具有普遍性，可应用于其他离散方程族.

可积耦合;二次型恒等式;Hamilton结构

1 引言

近年来，Lattice可积族成为可积系统理论研究的焦点，备受关注.许多非线性Lattice可积族［1－8］及其哈密顿结构的离散路径已经建立［8］，同时很多离散可积族的可积耦合的建立方法已被提到［9－14］.然而，如何建立一些离散可积族的哈密顿结构仍是非常重要和有趣的课题.郭福奎教授和张玉峰教授提出了二次型恒等式［15－16］，为建立连续可积耦合的Hamilton结构提供了理论依据.由于不存在换位运算，我们无法直接通过二次型恒等式直接得到离散可积耦合的Hamilton结构［15］.基于以上问题，我们尽力利用位移算子构建类似于连续可积族的换位运算，从而利用二次型恒等式得到离散可积族的Hamilton结构.

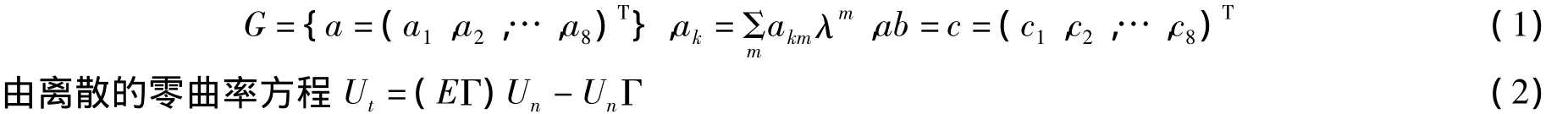
及其静态零曲率方程

若Γ1和ΓV2(3)同阶解满足Γ1=γΓ2，［a，b］T=aTR(b)，a，b∈，对称矩阵F=(fij)S×S，要求满足:

由二次型恒等式

构造李代数

其中

易证G满足矩阵乘法具有封闭性［10］.a=(a1，a2，…，a8)T，b=(b1，b2，…，b8)T.定义交换算子为

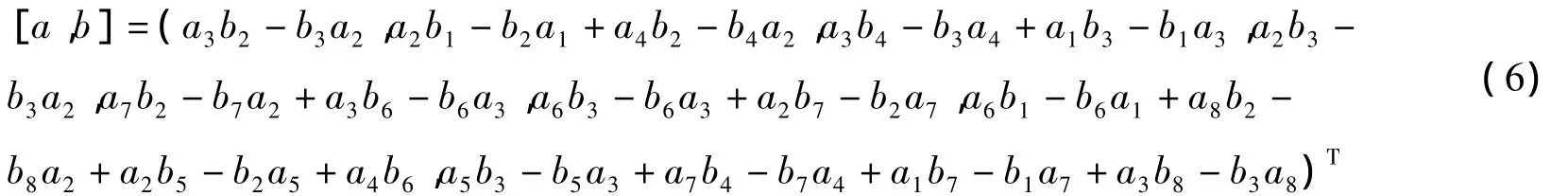
本文通过构造新的loop代数，借助于二次型恒等式得到了离散可积族的可积耦合及其哈密顿结构，这种方法非常新颖，可广泛应用于其他离散可积族.

2 Hamiltonian结构

设计对等谱问题

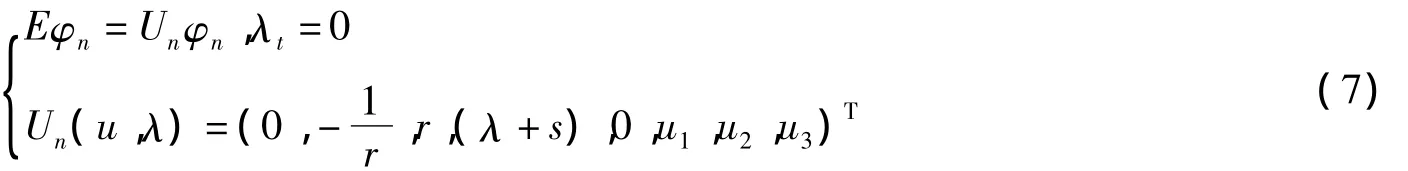
得递推关系

易证

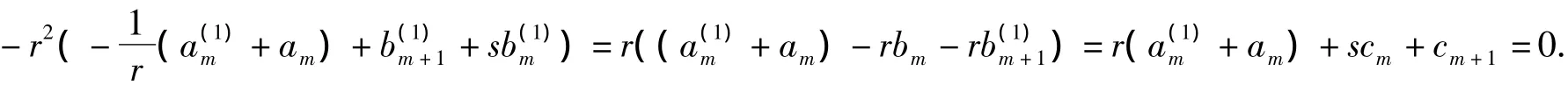
也就是说(9)中的第三个方程可由其他的推出来.

定义

方程(8)可以写成

直接计算得

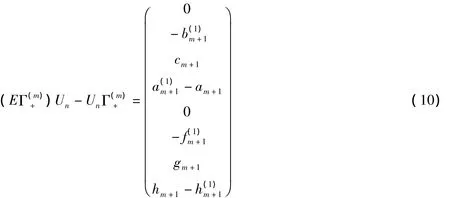
取Γ(m)=Γ(m)+，由零曲率方程Unt－(EΓ(m))Un+UnΓ(m)=0直接计算得

从(6)可得

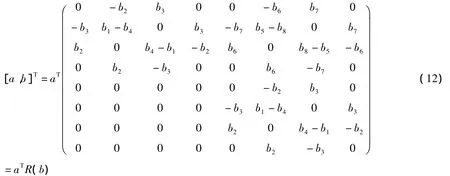
利用二次型恒等式，我们可求得对称矩阵

为建立(11)的哈密顿结构，规定

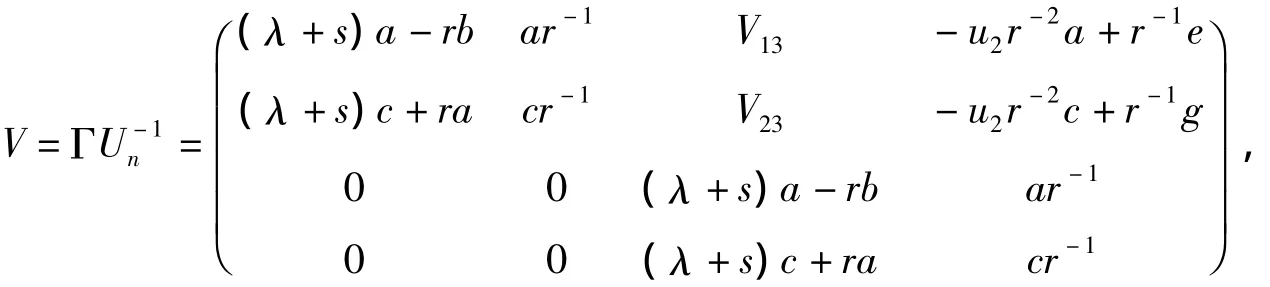
其中

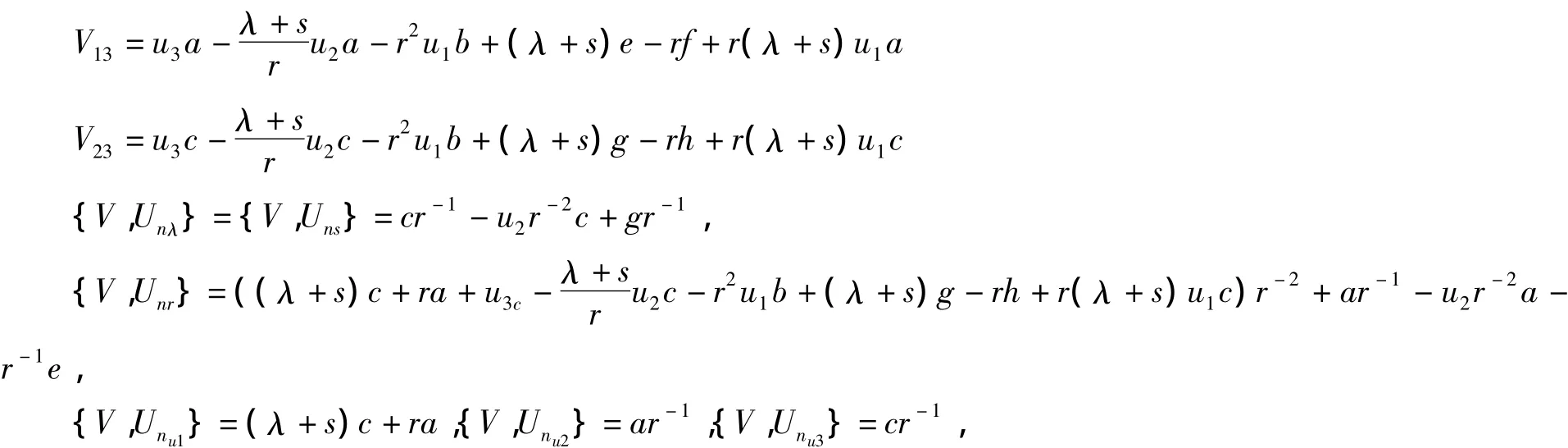
因此，利用二次型恒等式

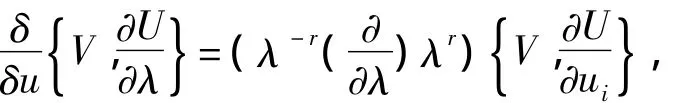
得

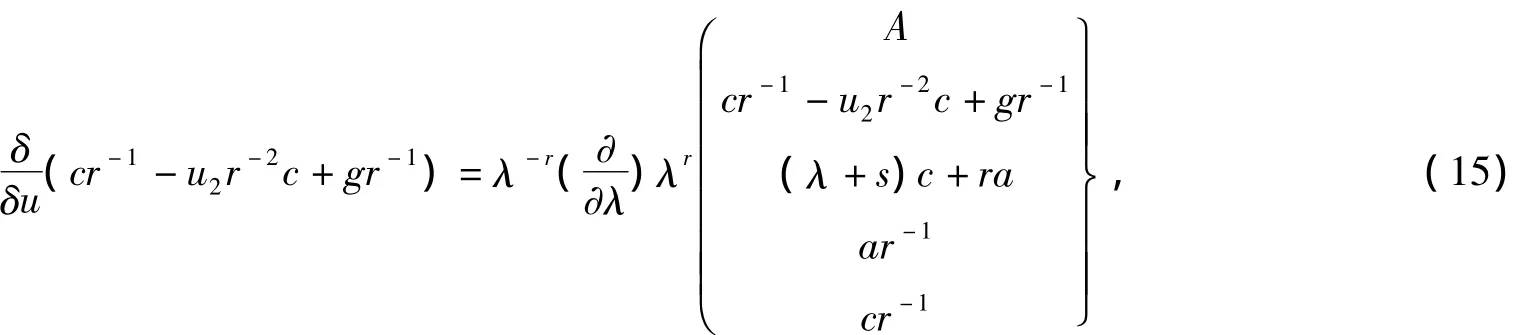
其中

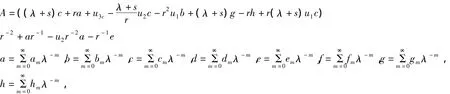
为确定常数γ，在上式两端令，n=0得γ=0，于是有

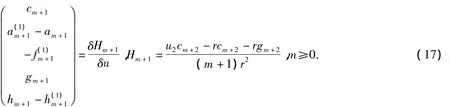
(11)可写成

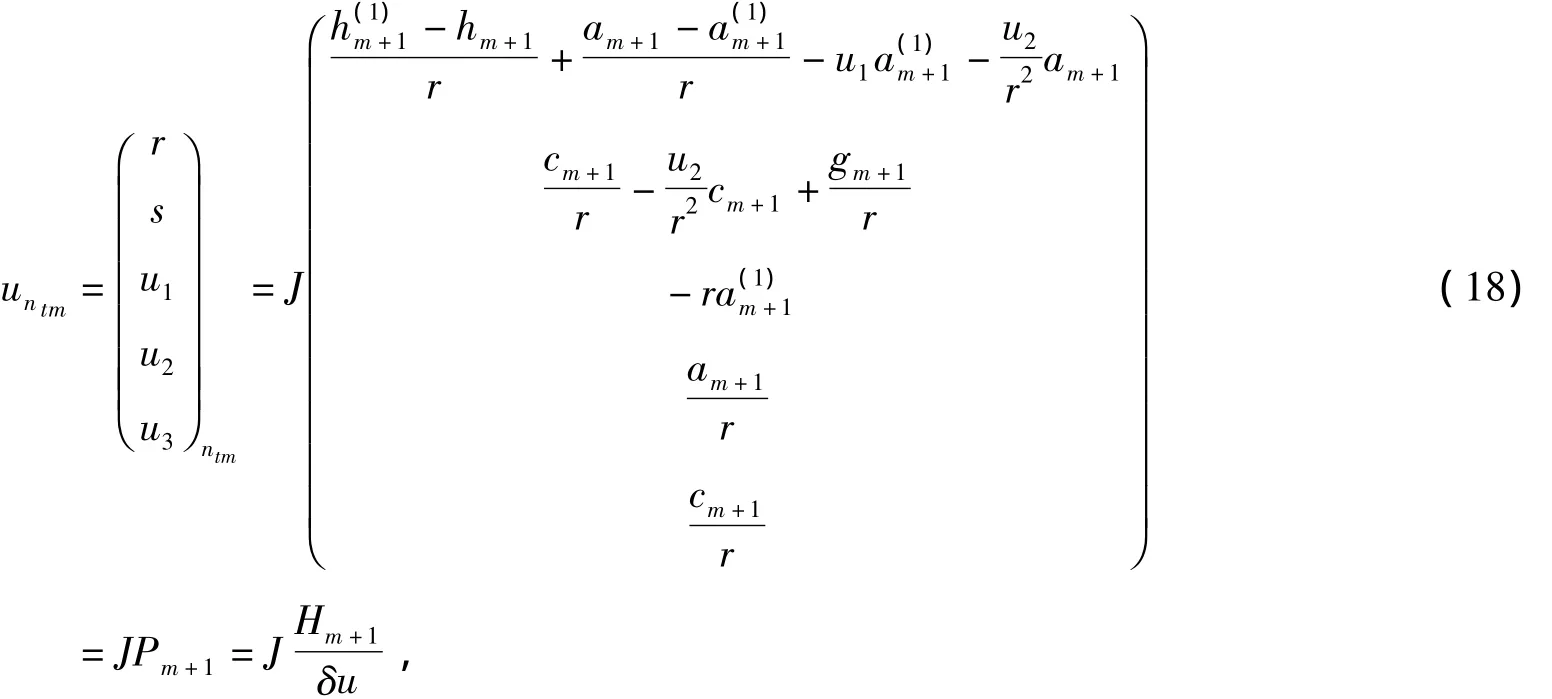
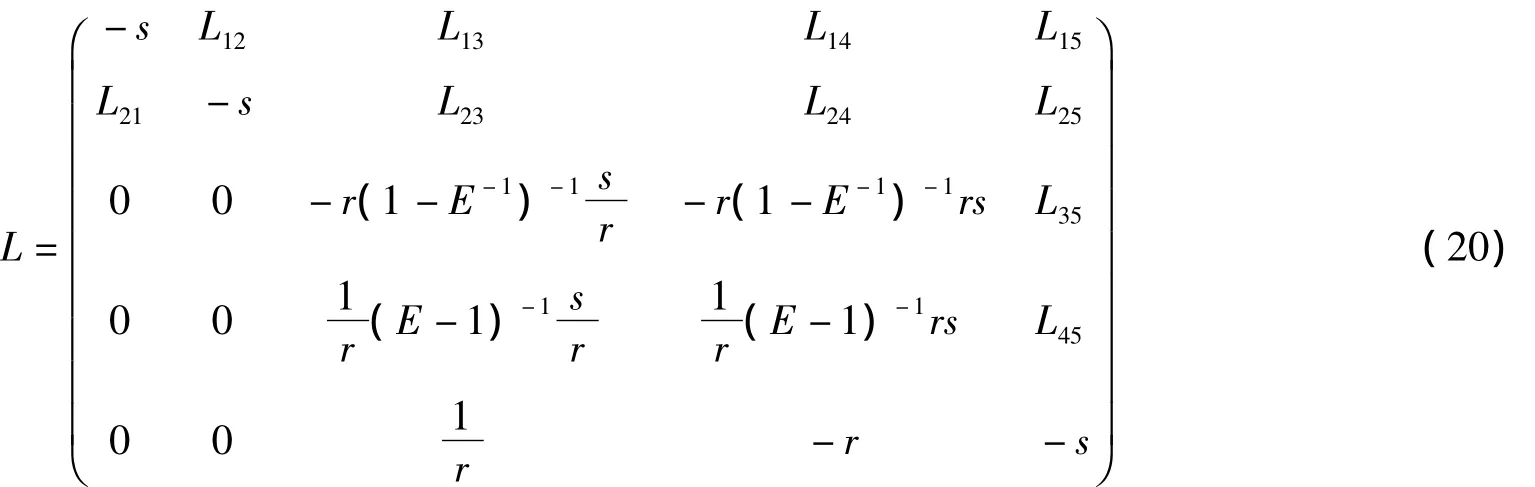
其中

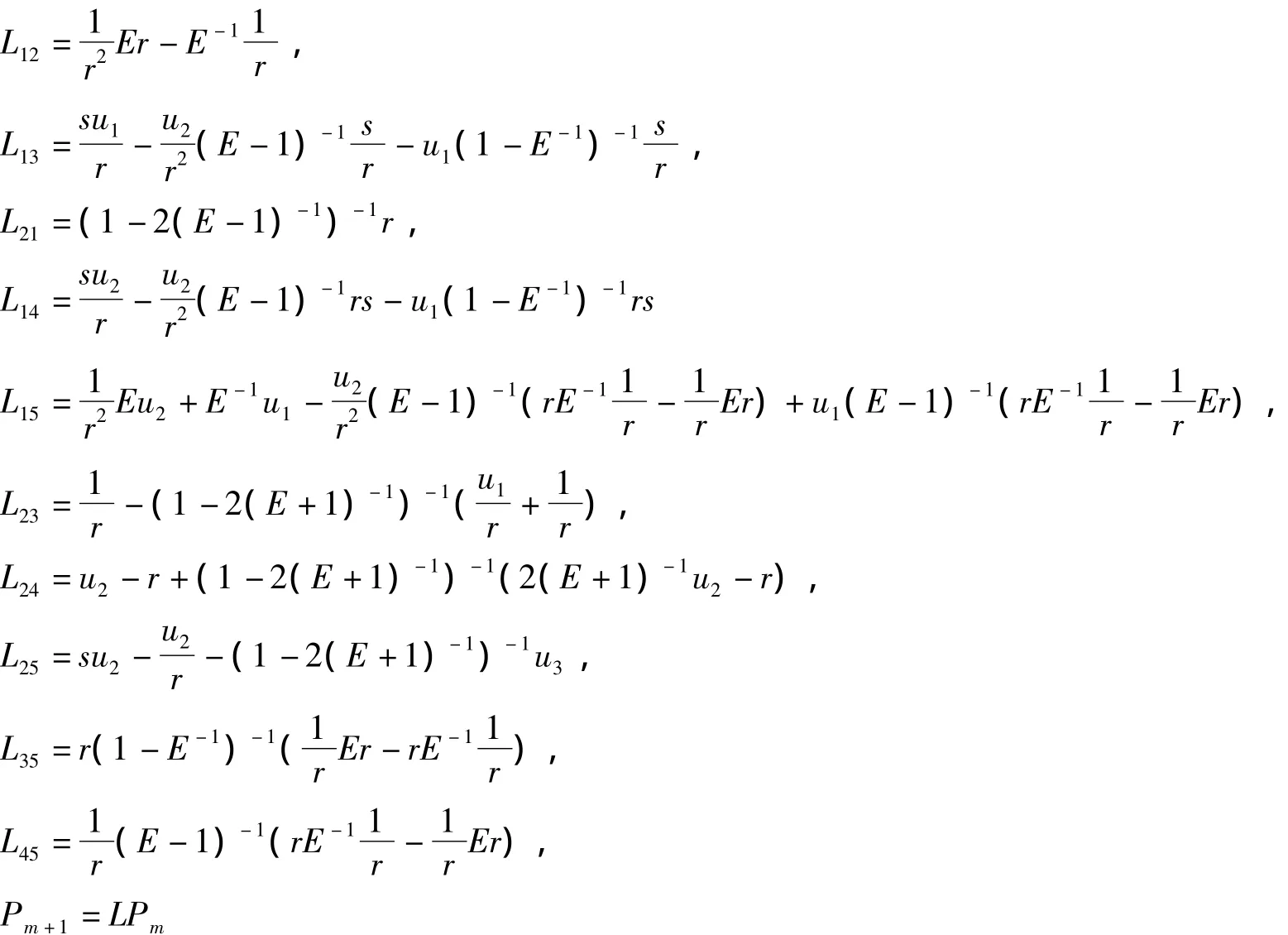
因此，(18)可写成Hamiltonian形式

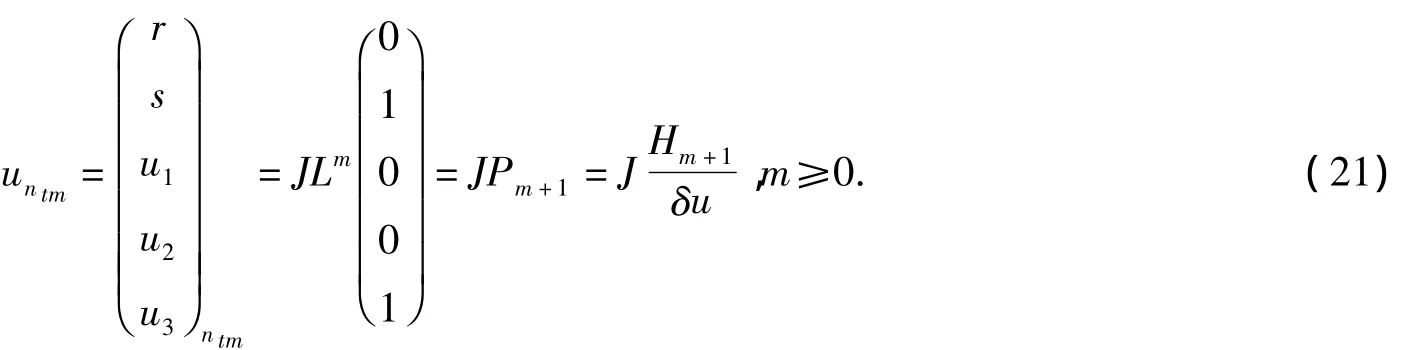
族(21)中的第一个非线性Lattice方程为

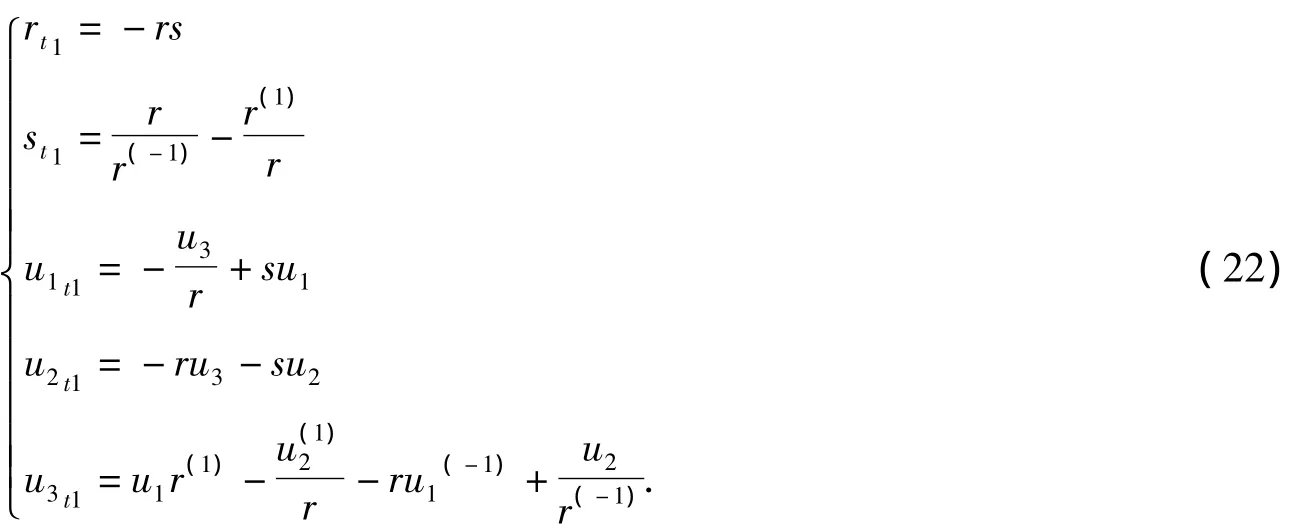
［1］Ablowitz Mark，Ladik.Nonlinear differential－difference equations［J］.J.Math.Phys.，1975(16):598－603.

［2］Bogoyavlensky Oleg.Integrable discretizations of the KdV equation［J］.J.Phys.Lett.A，1988，134(1):34－38.

［3］MaWenxiu，Xu Xixiang.Positive and negative hierarchies of integrable latticemodels associated with a Hamiltonian pair［J］.J.Internat Theoret.Phys.，2004，43(1):219－236.

［4］Narita Kazuaki.Soliton solutions for the coupled discrete KdV equations under nonvanishing boundary conditions at infinity［J］.J.Phys.Soc.Japan，2002，71(10):2401－2405.

［5］Xu Xixiang.A hierarchy of discrete Hamiltonian equations and its binary nonlinearization by symmetry constraint［J］.J.Phys.Lett.A，2004，326(3－4):199－210.

［6］Xu Xixiang，Zhang Yufeng.A hierarchy of Lax integrable lattice equations，Liouville integrability and a new integrable symplectic map［J］.J.Commun Theor.Phys.，2004，41(3):321－328.

［7］Tu Guizhang.A trace identity and itsapplication to the theory of discrete integrable systems［J］.J.Phys.A:Math.Gen.，1990(23):3903－3922.

［8］Xu Xixiang，Yang Hongxiang，Ding Haiyong.A Liouville integrable lattice soliton equation，infinitelymany conservation laws and integrable coupling systems［J］.J.Phys.Lett.A，2006，349(1－4):153－163.

［9］Zhang Yufeng，Fan Engui，Zhang Yongqing.Discrete integrable couplings associated with Toda－type lattice and two hierarchies of discrete soliton equations［J］.J.Phys.Lett.A，2006，357(6):454－461.

［10］Ma Wen－Xiu，Xu Xi－Xiang，Zhang Yufeng.Semidirect sums of Lie algebras and discrete integrable couplings［J］.J.Math.Phys.，2006，47(5):053501.

［11］Sun Ye－peng，Chen Deng－yuan，Xu Xi－xiang.Positive and negative hierarchies of nonlinear integrable latticemodels and three integrable coupling systems associated with a discrete spectral problem［J］.J.Nonlinear Anal.，2006，64(11):2604－2618.

［12］Xia Tiecheng，You Fucai，Chen Dengyuan.A generalized cubic Volterra lattice hierarchy and its integrable couplings system［J］.J.Chaos Solitons Fractals，2006，27(1):153－158.

［13］Ding Hai－Yong，Sun Ye－Peng，Xu Xi－Xiang.A hierarchy of nonlinear lattice soliton equations，its integrable coupling systems and infinitelymany conservation laws［J］.J.Chaos Solitons Fractals，2006，30(1):227－234.

［14］Guo Fukui，Zhang Yufeng.The quadratic－form identity for constructing the Hamiltonian structure of integrable systems［J］.J.Phys.A，2005，38(40):8537－8548.

［15］Guo Fukui，Zhang Yufeng.Expansion of the Lie algebra and its applications［J］.J.Chaos Solitons Fractals，2006，27(4):1048－1055.

［16］Zhang Yufeng，Yan Wang.A higher－dimensional Lie algebra and its decomposed subalgebras［J］.J.Phys.Lett.A，2006，360(1):92－98.

The Integrable Couplings of a Discrete Integrable Hierarchy and Its Hamiltonian Structure

XU Xiu－li
(Department of Senior Technology，Zaozhuang Vocational College of Science and Technology，Zaozhuang，277500，China)

The integrable couplings of a discrete integrable hierarchy and its Hamiltonian structure are obtained by the quadratic－form identity with shift operator.Thismethod can be used to produce the Hamiltonian structure of the other discrete integrable couplings.

integrable couplings;quadratic－form identity;Hamiltonian structure

O175.8

A

1672－2590(2015)03－0011－07

2015－03－27

徐秀丽(1982－)，女，山东枣庄人，枣庄科技职业学院高级技工部讲师.