全连续算子与拓扑度的相关证明及实例探究

祁琼

(南京财经大学应用数学学院，江苏南京 210046)

当x∈D时必有某yi使‖Ax－yi‖＜ε，故di(Ax)＞0，从而d(Ax)＞0.

全连续算子与拓扑度的相关证明及实例探究

祁琼

(南京财经大学应用数学学院，江苏南京 210046)

非线性泛函是现代数学研究中很重要的工具，非线性泛函分析包括拓扑度理论、半序方法、变分方法、分歧理论和Banach空间微分方程理论，本文讨论非线性算子的连续性与有界性，全连续算子与拓扑度相关性质的证明，并用实例证明相关结论.

非线性算子;连续性;有界性;全连续算子;拓扑度

1 前言

线性方程的基本问题是解的存在性和唯一性，而非线性方程的基本问题是解的存在性和多解性.而拓扑度理论是关于非线性方程的多解性的理论，因此对拓扑度的研究能帮助我们其粗略地确定非线性方程的个数.拓扑度理论是由L.E.J.Brouwer［1］在1912年创立的，他所建立的拓扑度针对的是有限维空间中的连续映射，即Brouwer度.全连续算子又称紧算子，是最接近于有限维空间上线性算子的一类重要算子.在线性代数中，关于线性变换所相应的线性方程组的求解问题已被完全解决了，因此研究全连续算子有利于对无穷维及非线性方程的求解问题.

2 全连续算子

2.1 连续性与有界性

对线性算子而言，连续性与有界性是等价的，而对非线性算子就没有这种等价性，连续算子不一定是有界的，现举例说明.

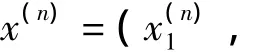
显然z(n)∈l2且‖z(n)‖=2，(n=1，2，…)，但f(z(n))=n→∞(n→∞).

2.2 全连续算子

____利用全连续算子定义［2］证明:设有界闭集(紧的)Ω⊂Rn，定义k(x，y，v)是Ω×Ω×R1上的连续函数，则积分算子K∶C(Ω)→C(Ω)，对∀Ψ∈C(Ω)，有(KΨ)(x)=∫K(x，y，Ψ(y))d y，则K是全连续算子.

证明:(分三步证明)

(1)证明K是紧算子

对∀Ψ∈B，∃C0＞0使得‖Ψ‖≤C0，因此，B∈C(Ω)是有界集.由k(x，y，v)在Ω×Ω×［－C0，C0］连续，则∃M＞0使得对∀(x，y，v)∈Ω×Ω×［－C0，C0］，有 K(x，y，v)≤M，故由定理Arzela－Ascoli定理［3］，

对∀x∈Ω，‖KΨ‖≤M，故K(B)在C(Ω)中有界.

(2)证明K(B)是等度连续的

∀ε＞0，∃δ＞0(δ=δ(ε))使得当‖x1－x2‖ ＜δ，x1，x2∈Ω，对于

又K(x，y，v)在Ω×Ω× [－C0，C0]连续，故K(x，y，v)在Ω×Ω× [－C0，C0]一致连续，从而有∀ε＞0，∃δ＞0使得‖x1－x2‖＜δ时，

故

(3)证明K是连续的

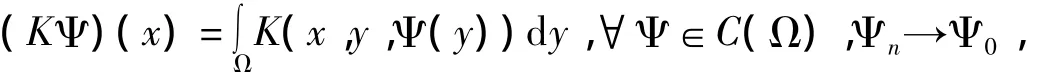
则

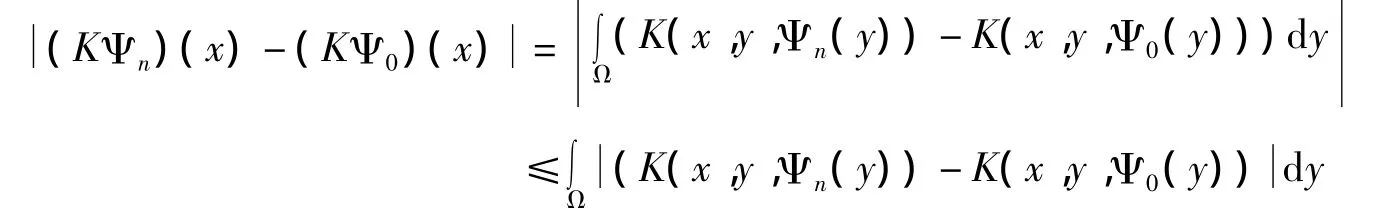
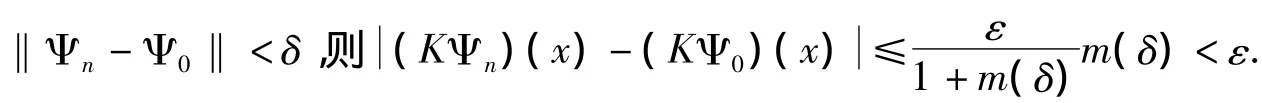
综上所述，K是全连续算子

2.3 全连续算子等价性的证明

设［4］A∶D→E2，且D是E2中的有界集，则下列三个结论是等价的:

(1)A∶D→E2全连续;

(2)∀ε＞0，∃Aε∶D→Eε连续有界，使对一切x∈D均有‖Ax－Aεx‖＜ε，这里Eε是E的某个有限维子空间;

证明:(1)→(2):由假定，A(D)是E2中列紧集，故对于给定的ε＞0，∃y1，…，ym∈A(D)，构成A (D)的有限ε－网，用Eε表由y1，…，ym张成的有限维子空间.∀y∈E2，令

显然di(y)非负连续，且只在球‖y－yi‖＜ε内为正.

令

当x∈D时必有某yi使‖Ax－yi‖＜ε，故di(Ax)＞0，从而d(Ax)＞0.

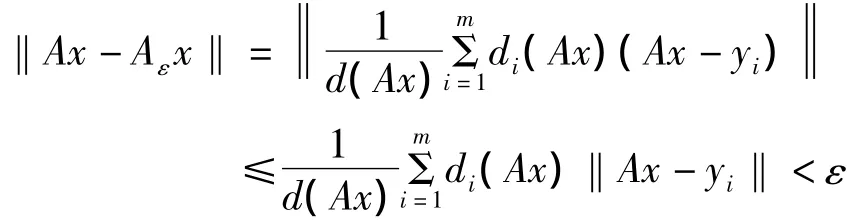
由于A(D)列紧，故A(D)有界，从而∃M＞0，使‖Ax‖≤M，∀x∈D;而‖Ax‖≤M+ε，∀x∈D;故Aε有界.

(2)→(3):由假定，∃B ∶D→H连续有界，H表E的某有限维子空间，使

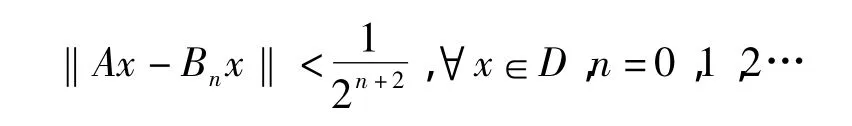
令A0=B0，A1=B1－B0，…，An=Bn－Bn－1，…显然，当n=1，2，…时，An∶D→，这里

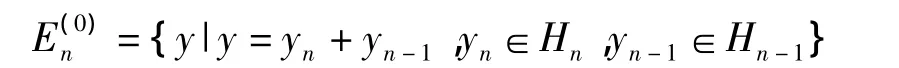
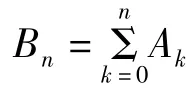
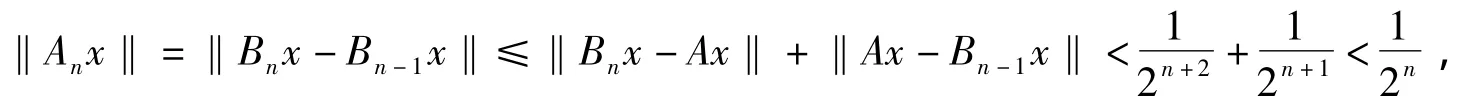
An(n=0，1，2，…)的连续性和有界性是显然的.

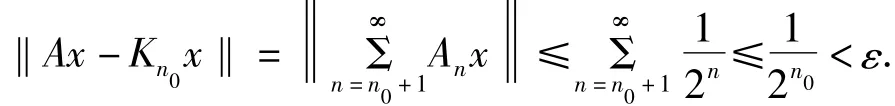
3 拓扑度

3.1 拓扑度相关性质证明

定理［5］:由拓扑度定义［5］所定义的deg(f，Ω，p)具有下列四条基本性质:

(i)正规性:若p∈Ω，则deg(f，Ω，p)=1，这里I为单位算子;

(iii)区域可加性:设Ω1，Ω2⊂Ω是Rn中的有界开集，Ω1∩Ω2=Ø，并且对任给的x∈(Ω1∪Ω2)，都有f(x)≠p，则必有

(iv)平移不变性:deg(f，Ω，p)=deg(f－p，Ω，p)

证明:

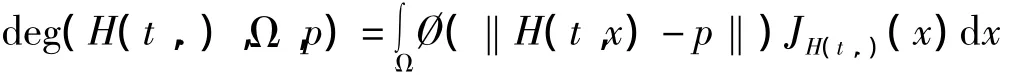
由上式知deg(H(t，.)，Ω，p)关于t是连续的.

事实上，由Ø(‖H(t，x)－p‖)JH(t，.)(x)在［0，1］×上连续并且是紧的，故复合函数一致收敛，i.e，∀ε＞0，∃δ＞0，使得当＜δ及‖x1－x2‖＜δ时，有

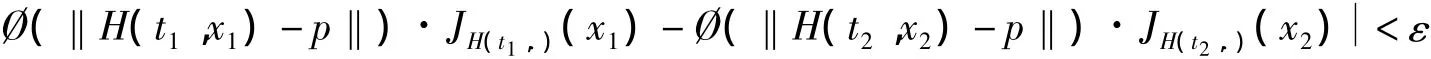
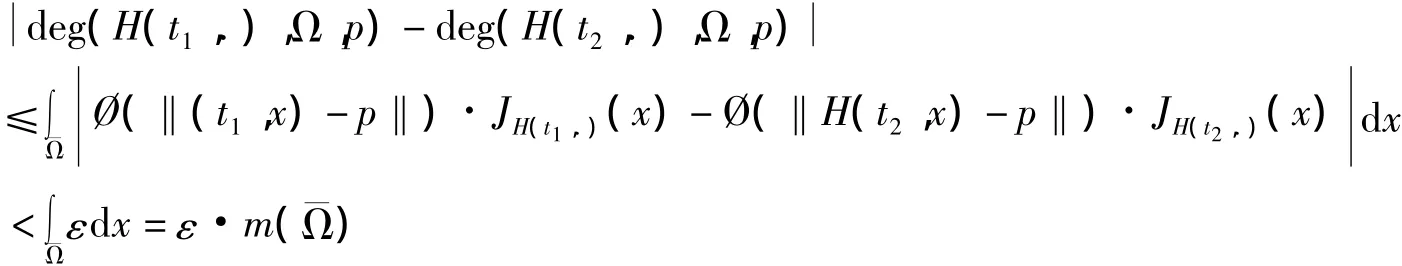
所以deg(H(t，.)，Ω，p)关于t是连续的.

得证.

(iv)利用定义［5］

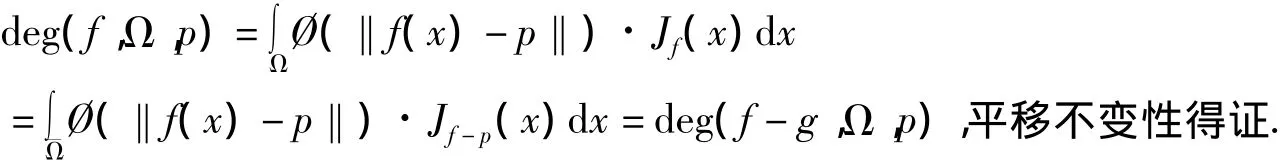
3.2 举例

满足拓扑度定义的连续非负函数

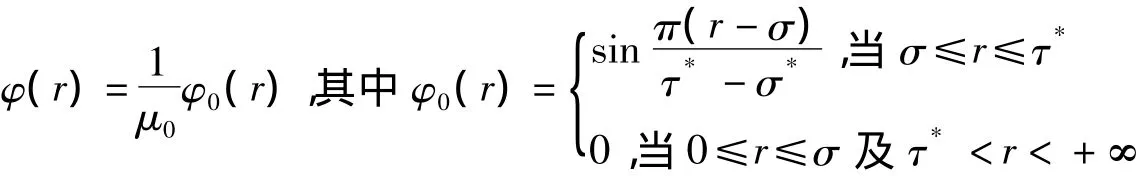
4 结论

本文对全连续算子及拓扑度相关定义及性质给出了较为简洁的证明，并用相关实例对定义及性质做出了进一步的阐释，方便理解非线性泛函的基本知识，为之后更深层次的学习打下基础.

［1］Brouwer，L.EJ.Invarianz des n－dimensionalen Gabiets［J］.Math Ann，1912(71):305－313.

［2］郭大钧.非线性泛函分析(第2版)［M］.济南:山东科学技术出版社，2001.

［3］孙经先.非线性常微分方程泛函方法［M］.北京:科学技术出版社，2008.

［4］郭大钧，孙经先，刘兆里.非线性常微分方程泛函方法［M］.济南:山东科学技术出版社，2005.

［5］陈文塬.非线性泛函分析［M］.兰州:甘肃人民出版社，1982.

The Related Proof and Case Study of Completely Continuous Operator and Topological Degree

QIQiong
(School of Applied Mathematics，Nanjing University of Finance and Economics，Nanjing，210046，China)

Nonlinear functional analysis is an important tool in the study ofmodern mathematics.Nonlinear functional analysis includes the theory of topological degree，the semi ordermethod，the variationalmethod，the theory of bifurcation and differential equation theory in Banach space.The paper discusses how to prove the related properties of continuity and boundedness of nonlinear operator，completely continuous operator and topological degree.Igive examples to prove the conclusions.

nonlinear operator;continuity;boundedness;completely continuous operator;topological degree

O177

A

1672－2590(2015)03－0006－05

2015－04－09

祁 琼(1989－)，女，江苏南京人，南京财经大学应用数学学院硕士研究生.