基于换乘最优的城市圈城际铁路运行图研究

李智，张琦，袁志明

（中国铁道科学研究院通信信号研究所，北京100081）

基于换乘最优的城市圈城际铁路运行图研究

李智，张琦*，袁志明

（中国铁道科学研究院通信信号研究所，北京100081）

城市圈城际铁路是中国铁路未来发展的重点之一.在城际铁路间换乘所需换乘等待时间的长短是影响乘客满意度的重要因素.因此，在编制城际铁路列车运行图的过程中，应设法减少乘客的换乘等待时间并尽量不使乘客错过换乘.本文对具体换乘过程进行分类并详细分析，提出列车延迟时间和乘客换乘走行时间的概率分布，并据此计算乘客换乘等待时间.在周期事件规划问题（PESP）相关理论的基础上，本文提出基于换乘最优的城际铁路周期运行图编制模型，并以某城市圈的城际铁路网为例，验证该模型的可行性.结果表明，根据该模型编制的列车运行图可以显著地减少乘客换乘等待时间，从而提高乘客满意度.

铁路运输；城际铁路运行图；周期事件规划问题；换乘等待时间；周期运行图

1 引言

在国家未来铁路建设规划中，除了加大路网密度外，重点是各城市圈中的城际铁路.典型的城市圈城际铁路是以一到两个核心城市为中心，以辐射状连接周围100 km以内的卫星城市及机场、重要旅游景点等.其主要功能是满足乘客在它们之间的通勤、购物、旅游等需求.

和其他铁路运输产品不同的是，城际铁路面临其他交通方式的激烈竞争.为了吸引乘客，在编制城际铁路运行图时，要紧紧抓住乘客的需求，提高乘客满意度，而不是像既有铁路那样“强迫”乘客服从于铁路的时间表.与既有铁路不同的是，城际铁路网中会有不可忽视的换乘客流.换乘时间一般是指乘客从一条线路的前次列车下车时起至登上另一条线路的接续列车时止的时间间隔，该时间间隔可以分为两部分，一部分是乘客的换乘走行时间，一部分是乘客的换乘等待时间[1].

换乘等待时间的长短是乘客满意度的重要影响因素.随着换乘等待时间的增多，乘客满意度会随之降低.如果因为列车晚点而使乘客错过换乘，乘客只能等待下一趟开往同样目的地的列车进行换乘，这样就会严重影响乘客满意度.因此，在编制城际铁路列车运行图时，应设法减少乘客的换乘等待时间并尽量不使乘客错过换乘.

目前，国内外学者在研究列车运行图的过程中[2，3]，由于模型规模所限，列车之间的接续只是作为一个粗略的约束条件.然而，换乘等待时间的长短是乘客满意度的重要影响因素，其细节亟待进行深入研究.本文通过研究乘客的换乘等待时间，编制便于乘客换乘的城际铁路周期运行图.

2 换乘问题的相关理论及分析

2.1 理想情况下的换乘

列车在区间运行时，其站间实际运行时间总是大于站间最小运行时间，为了确保列车准点率，在编制列车运行图时，站间图定运行时间往往被设定为站间最小运行时间与给定的缓冲时间之和.在本文分析中，站间最小运行时间已包含列车的启停附加时分.本文定义可换乘的列车之间的图定接续时间为可用换乘时间，用tm表示；tp为列车A在车站Ⅰ、Ⅱ之间的图定运行时间；tr为列车A在车站Ⅰ、Ⅱ之间的最小运行时间;ts为列车A在车站Ⅰ、Ⅱ之间的实际运行时间;tb为车站Ⅰ、Ⅱ之间的缓冲时间;tc为乘客在车站Ⅱ从列车A换乘到列车B所需的换乘走行时间；t0为列车A在车站Ⅰ的计划出发时刻；t1为列车A在车站Ⅱ的计划到达时刻为列车B在车站Ⅱ的计划出发时刻.在理想情况下，列车的站间实际运行时间等于其图定运行时间，并且换乘的两列车之间的可用换乘时间恰好等于乘客的换乘走行时间，这种情况下乘客的换乘等待时间为零.图1表示理想情况下乘客从列车A换乘到列车B的具体过程.

图1 理想情况下换乘示意图Fig.1 Ideal transfer diagram

2.2 实际情况下的换乘

在实际情况下，主要有三方面的因素导致其偏离理想情况.

首先，由于司机驾驶习惯、车况、天气等客观因素，列车实际运行时间不是一个定值.本文定义列车在站间的实际运行时间多出站间最小运行时间的部分为延迟时间，用td表示.

其次，由于年龄，身体状况，运动习惯的不同，不同乘客的换乘走行时间也不是定值.

最后，列车运行图的编制工作要考虑到多方面的因素，难以保证每对可换乘的列车之间的接续时间都较为合理.

2.3 换乘等待时间分析

在实际情况下的换乘过程中，对于乘客乘坐列车A在车站Ⅱ换乘列车B，根据列车A在车站Ⅱ的延迟时间及乘客换乘走行时间的不同，存在以下四种具体情况：

（1）列车A在图定运行时间之内到达，列车未晚点.乘客经过换乘走行时间tc之后到达列车B所在站台，经换乘等待时间tw之后换乘到列车B，换乘过程如图2所示，换乘等待时间tw如式（1）所示.

图2 情况一换乘示意图Fig.2 The first transfer circumstance diagram

（2）列车A晚于计划到达时刻到达，即列车晚点.但在这种情况下，乘客经过换乘走行时间tc之后到达列车B所在站台后，列车B还未出发，乘客经换乘等待时间tw之后仍可以成功换乘到列车B，换乘过程如图3所示，换乘等待时间tw如式（2）所示.

（3）列车A晚于计划到达时刻到达，乘客经过换乘走行时间tc之后到达列车B所在站台后，列车B已经出发，此时乘客错过换乘原计划的列车B，需要在车站Ⅱ等待下一班到同样目的地的接续列车换乘，换乘过程如图4所示，ΔtB为接续列车的发车间隔为下一班接续列车在车站Ⅱ的计划出发时刻.换乘等待时间tw如式（3）所示.

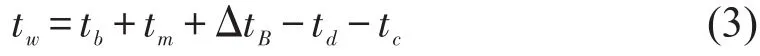
图3 情况二换乘示意图Fig.3 The second transfer circumstance diagram

图4 情况三换乘示意图Fig.4 The third transfer circumstance diagram

（4）列车A在图定运行时间之内到达，列车未晚点.但在这种情况中，乘客经过换乘走行时间tc之后到达列车B所在站台时，列车B已经出发，此时乘客错过换乘原计划的列车B，需要在车站Ⅱ等待下一班到同样目的地的接续列车换乘，换乘过程如图5所示，换乘等待时间tw如式（4）所示.

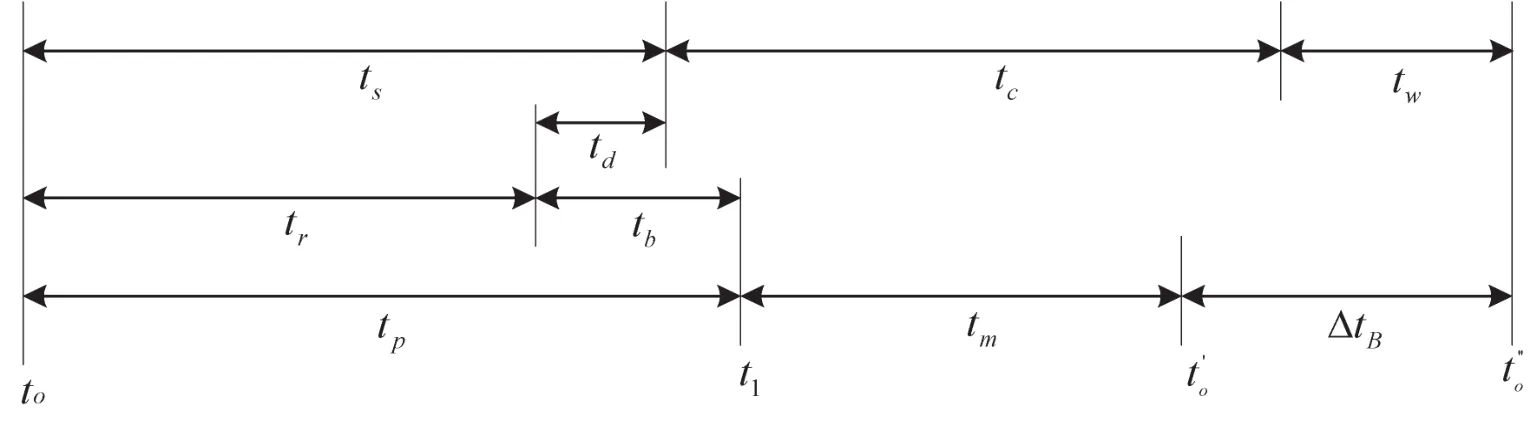
图5 情况四换乘示意图Fig.5 The fourth transfer circumstance diagram

在情况（3）和情况（4）中，错过两次或更多接续列车的情况可依同样规律计算，但该情况发生的可能性很小，本文不做考虑.

当乘客错过换乘时，就要等待下一班开往同样目的地的接续列车，而此时乘客实际感受到的延误时间是换乘时相对于旅行计划所多出的时间，即下一班接续列车与原计划接续列车的发车间隔ΔtB.因此，情况（3）和情况（4）中的换乘等待时间不能单纯的用式（3）进行计算，而要使用下一班接续列车与原计划的接续列车之间的发车间隔，即

综上，乘客的换乘等待时间用式（6）表示.

3 延迟时间和换乘走行时间的概率分布

由第2节的分析可知，列车运行图编制完成后，换乘等待时间tw的值取决于列车的延迟时间td和乘客的换乘走行时间tc，且两者均不为定值.因此，需要用统计学中的概率分布来表示它们的取值，并以此计算换乘等待时间期望.

3.1 列车延迟时间的指数分布模型

为了保证列车的正点率，需要设定合理的缓冲时间tb.为此，首先要对延迟时间td进行研究.有学者研究表明，延迟时间td符合指数分布模型[4]，其概率密度函数如式7所示.λ是延迟时间的期望，也就是该列车的平均延迟时间.这个数据可以从运营部门提供的数据中得到.

列车准点率可由延迟时间概率密度函数的积分求得.由此可以根据所需的列车准点率设定缓冲时间tb.如所需的准点率为90%，则可对tb取值使得P(td＜tb)=90%，保证90%的列车正点到达.

3.2 乘客换乘走行时间的条件分布模型

在众多的研究中，乘客走行时间被当成定值来研究[2,5].而实际上，相比于列车延迟时间，乘客走行时间的波动性往往更大，前者的影响一定程度上可以被后者的影响所“淹没”.在铁路换乘中，尚未有乘客换乘走行时间的研究，而关于城市轨道交通的众多研究表明，乘客换乘走行时间的分布呈偏态，一般用对数正态分布来表示[1,6]，如式（8）所示.

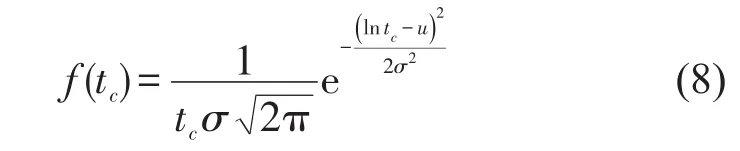
在给定tc的期望E(tc)与方差var(tc)的前提下，由对数正态分布性质，可得：

因此，可给定换乘走行时间的平均值（期望）和方差，得出其概率分布.

然而，乘客在铁路中的换乘走行时间的变化规律与在公交、地铁中的换乘走行时间的变化规律有着一定的区别.铁路有着固定、公开的时刻表，若前次列车晚点，则乘客换乘时会加快脚步，尽量赶上接续列车，反之亦然，因此乘客换乘走行时间会对延迟时间起反馈作用，乘客换乘走行时间的概率分布为条件分布，与延迟时间td有着关联性.本文基于上述对数正态分布模型，定义换乘走行时间的期望如式（11）所示.

式中Ec定义为正点换乘走行时间均值，即为前次列车正点到达时，乘客换乘走行时间的期望；体现出了乘客换乘走行时间对延迟时间的回馈；α为一常数，取值范围在(0,1)之间.

因此，乘客走行时间tc的概率分布为条件概率分布，即为

式中u，σ2可由式（9）–式（11）求得.

3.3 延迟时间和换乘走行时间的联合概率分布

根据条件概率的性质，f(tc,td)=f(tc|td)∙f(td)，则延迟时间和换乘走行时间的联合概率分布如式（13）所示.

4 加权换乘等待时间及其期望值

4.1 加权换乘等待时间

与不换乘就能到达目的地相比，换乘乘客的满意度会下降.然而乘客在成功换乘的情况下，旅行计划未改变，因此从心理上较容易接受换乘等待时间.但若错过换乘，乘客的旅行计划就会延误，乘客从心理上很难接受换乘等待时间.因此在建立模型时，对这两种情况下的换乘等待时间不能“平等对待”.基于此，本文定义加权换乘等待时间，对这两种情况下的换乘等待时间赋以相应的权重ηs和ηf，用Tw来表示加权换乘等待时间，如式（14）所示.

4.2 加权换乘等待时间期望

由式（14）可得，加权换乘等待时间tw是关于延迟时间td和换乘走行时间tc的分段函数，而td、tc的联合概率分布函数已在式（13）中求得，因此，可得加权换乘等待时间的期望，如式（15）所示.式（15）较为复杂，在实际运用过程中可用Matlab等软件计算.

5 基于换乘最优的周期运行图编制模型

5.1 模型建立背景

城际铁路的线路情况与列车种类都比较简单，其运营方式为“高密度，小编组，公交化”，具有明显的周期性的特点，适合使用周期运行图.对于周期运行图，许多学者在PESP（周期事件规划问题）的基础上进行研究，取得了很不错的成果[1,7，8].然而我国客运专线完全成网之后，路网规模大，运距长，跨线运行多，此时周期运行图就不一定适用[9].而城际铁路却不具有这些复杂性，因此可以基于PESP理论建立模型，编制城际铁路周期运行图.

5.2 模型研究对象

换乘发生于两列列车之间，本文把具有合理接续的列车对作为研究对象，若列车B在某站为列车A的接续列车且它们之间的接续时间不小于正点走行时间均值，且列车B与列车A的后一班列车，列车B的前一班列车与列车A均不接续或接续时间小于正点走行时间均值，则定义列车A，列车B为一对换乘列车.本文模型中考虑换乘列车之间的加权换乘等待时间.

5.3 模型的目标函数

在城际铁路中，线路情况和列车种类都比较简单，以往编制运行图所考虑的总旅行时间不再是研究的重点，而换乘等待时间很大程度上影响了乘客满意度.因此，文中模型的目标函数为所有乘客的加权换乘等待时间最小.

在上文的研究中，以列车的角度研究了换乘等待时间，但不同线路之间，换乘乘客的数量亦不同，因此要计算乘客感受到的换乘等待时间，必须考虑乘客数量.本文提出换乘客流量的概念，把换乘列车之间的日平均换乘人数定义为换乘客流量，用Nt表示，该值可由客流统计得出.而换乘列车的换乘客流量和换乘列车的加权换乘等待时间的乘积即为换乘列车的乘客加权换乘等待时间.

综上，本文模型以一个列车运行图周期内（不同线路周期不同则取周期的最小公倍数），对于所有线路的全部换乘列车，乘客加权换乘等待时间之和最小为目标函数，如式（16）所示.

式中m为一个周期内所有线路之间换乘列车的数量；(Nt)i为第i对换乘列车的换乘客流量；E(Tw)i为第i对换乘列车的加权换乘等待时间期望，其可由式（8）–式（12）得出.

5.4 模型的约束条件

根据PESP理论及本文提出的换乘列车的定义，模型的约束条件为式（17）–式（24）.

式（17）–式（19）为5.2节提出的换乘列车的定义约束.列车A与列车B为一对换乘列车；列车B'为列车B的前一班列车；列车A*为列车A的后一班列车；线路为列车A在s站的到达时间为列车A在s站的出发时间；为乘客从列车A换乘到列车B的正点换乘走行时间均值.

式（20）–式（24）是基于PESP理论的列车运行约束.Tl是列车所在线路l的运行图周期，一般取60m in或120m in；pt为常数，为1或0.其中：式（20）为线路l上的列车A在s站和t站之间的图定运行时间约束为列车A在s站和t站之间的最小运行时间（已包含起停附加时分）为列车A在s站和t站之间的缓冲时间.式（21）为列车在s站的停站时间约束为列车在车站s的停站时间的最小值和最大值.式（22）为线路l上的始发站s站的始发车间隔约束.为了方便乘客，列车在周期运行图上要呈现出一定程度的均匀性，在始发站的发车间隔既不能过小，也不能过大. fl,min和fl,max分别为线路l始发站的最小发车间隔和最大发车间隔.式（23）和式（24）为线路l上的安全间隔约束.hd为相邻列车在s站的最小安全发车间隔时间；ha为相邻列车在s站的最小安全接车间隔时间.

6 基于换乘最优的列车周期运行图编制案例

本文以某建设中的城市圈城际铁路为例，通过比较原运行图和本文模型优化后运行图的乘客加权换乘等待时间之和，来验证该模型的可行性.该城市圈城际铁路如图6所示.以城市圈的中心车站O为中心已建成3条城际线路l1，l2与l3.这三条线路上运行的列车分为直达列车和站站停列车.线路l1的列车运行图周期为2 h，一个周期内计划发行直达列车3对，站站停列车3对，两种列车交替运行.线路l2的列车运行图周期为1 h，一个周期内计划发行直达列车3对，站站停列车2对.线路l3的列车运行图周期为1 h，一个周期内计划发行直达列车1对，站站停列车1对.

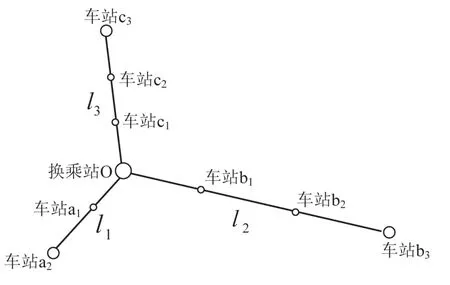
图6 某城市圈城际铁路示意图Fig.6 The intercity railway network diagram ofone urban circle

本例中，由于三条线路运行周期的最小公倍数为2 h，则研究三条线路的2 h运行图.根据本文定义，2 h内三条线路之间共有28对换乘列车.对成功换乘的权重因子ηs取2，错过换乘的权重因子ηf取3，根据线路相关数据及优化之前的三条线路的运行图，计算出原有乘客加权换乘等待时间总和Z=44 963.5m in.而将三条线路的相关数据代入本文模型并用Matlab软件进行求解后，得出目标函数值为Z=27 532.1m in.新编制的运行图在满足线路的各类约束条件的同时，乘客加权换乘等待时间减少40%左右，这就意味着乘客的换乘等待时间较之前明显减少.因此，本文模型优化后的运行图可以有效地减少乘客的换乘等待时间，从而提高城际铁路的乘客满意度.

7 研究结论

本文主要研究了基于换乘最优的城市圈城际铁路周期运行图编制方法，结合城际铁路的实际情况，详细分析了不同换乘情况的具体过程，提出了列车延迟时间和乘客换乘走行时间的概率分布，并据此计算乘客换乘等待时间，结合PESP的相关理论提出基于换乘最优的城市圈城际铁路周期运行图编制模型.最后算例验证的结果表明，根据本文模型优化后的列车运行图可以有效地减少乘客的换乘等待时间，从而提高城际铁路的乘客满意度.

[1]杜鹏,刘超,刘智丽.地铁通道换乘乘客走行时间规律研究[J].交通运输系统工程与信息,2009,9(4):103-109.[DU P，LIU C,LIU Z L.Walking timemodeling on transfer pedestrians in subway passages[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(4):103-109.]

[2]谢美全,聂磊.周期性列车运行图编制模型研究[J].铁道学报,2009,31(4):7-13.[XIEM Q,NIE L.Model of cyclic train timetable[J].Journal of The China Railway Society,2009,31(4):7-13.]

[3]Peeters L,Kroon L G.A variable trip time model for cyclic railway timetabling[J].Transportation Science. 2003,37（2）:198-212.

[4]Goverde R M P.Optimal scheduling of connections in railway systems[C].The Eighth WCTR,Antwerp, Belgium,1998.

[5]Vansteenwegen P,Oudheusden V D.Developing railway

timetableswhich guarantee a better service[J].European JournalofOperationalResearch,2006(173):337-350.

[6]何韬,毛保华,杨远舟.地铁换乘站线路间列车到站间隔优化问题研究[J].物流技术,2011,30(6):118-121. [HE T，MAO B H,YANG Y Z.Optimization of arrival intervals at metro interchange stations[J].Logistics Technology,2011,30(6):118-121.]

[7]Nachtigall K,Voget S.Minimizing waiting times in integrated fixed interval timetables by upgrading railway tracks[J].European Journal of Operational Research, 1997,103(3):610–627.

[8]Goverde R M P.Improving punctuality and transfer reliability by railway timetable optimization[C]. Proceedings of TRAIL 5th Annual Congress,Delft, Netherlands,1999.

[9]时颢.我国高速铁路列车运行图采用模式的分析[J].铁道学报,2000,22(1):92-97.[SHI H.Analysis on rational applied modes of high-speed train diagram in our country[J].Journal of the China Railway Society, 2000,22(1):92-97.]

Optimal Transfer of Intercity Railway Train Diagram

LIZhi,ZHANGQi,YUAN Zhi-m ing

(Signal&Communication Research Institute,China Academy of Railway Sciences,Beijing 100081,China)

The intercity railway in urban circles is one of the key parts of China’s railway development in the future.The transfer waiting time of intercity railway transfer is an important factor influencing the satisfaction of passengers.Therefore,when establishing the intercity railway train diagram,reducing the transferwaiting time of passengers and trying not tomake passengers tomiss their transfer should be taken into consideration.This paper makes a concrete analysis of the transfer process，puts forward probability distributions of the train delay time and passenger transfer walking time and calculates the transfer waiting time.Based on the periodic event schedule problem model(PESP),amodel based on optimal transfer is put forward and applied to a case study.The result shows that the train diagram developed by themodel can effectively reduce the transferwaiting time,thereby improving the satisfaction of passengers.

railway transportation;intercity railway train diagram;periodic event schedule problem; transferwaiting time;periodic train diagram

1009-6744（2015）03-0114-06

U292.4

A

2015-01-27

2015-04-10录用日期：2015-04-15

中国铁路总公司科技研究开发计划重点课题（2014X004-A）.

李智（1988-），男，河南郑州人，博士生.＊通信作者：13801299078@139.com